Giaitoan.edu.vn xin giới thiệu lời giải chi tiết bài tập 4 trang 74 SGK Toán 9 tập 2 - Chân trời sáng tạo. Bài viết này sẽ giúp học sinh nắm vững kiến thức, hiểu rõ phương pháp giải và tự tin làm bài tập.
Chúng tôi cung cấp đáp án chính xác, dễ hiểu cùng với các bước giải cụ thể, giúp bạn học Toán 9 một cách hiệu quả nhất.
Cho hình vuông MNPQ nội tiếp đường tròn bán kính R. Tính độ dài cạnh và đường chéo của hình vuông theo R.
Đề bài
Cho hình vuông MNPQ nội tiếp đường tròn bán kính R. Tính độ dài cạnh và đường chéo của hình vuông theo R.
Video hướng dẫn giải
Phương pháp giải - Xem chi tiết
- Đọc kĩ dữ liệu để vẽ hình.
- Dựa vào: Đường tròn ngoại tiếp hình vuông có tâm là giao điểm của hai đường chéo và có bán kính bằng nửa đường chéo.
Lời giải chi tiết
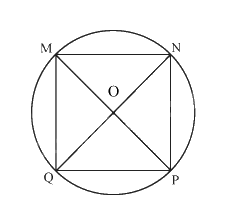
Vì hình vuông MNPQ nội tiếp. O là giao điểm của MP và NQ
Suy ra R = OM = \(\frac{{MP}}{2}\). Do đó MP = 2R.
Ta có MN2 = OM2 + ON2 = R2 + R2 = 2R2
Suy ra MN = \(R\sqrt 2 \).
Vậy hình vuông MNPQ có độ dài cạnh là \(R\sqrt 2 \), đường chéo là 2R.
Bài tập 4 trang 74 SGK Toán 9 tập 2 - Chân trời sáng tạo thuộc chương trình học Toán 9, tập trung vào việc vận dụng kiến thức về hàm số bậc nhất và hàm số bậc hai để giải quyết các bài toán thực tế. Bài tập này yêu cầu học sinh phải hiểu rõ các khái niệm về hệ số góc, giao điểm của đồ thị hàm số và cách xác định phương trình đường thẳng.
Trước khi đi vào giải bài tập, chúng ta cần phân tích kỹ đề bài để xác định rõ yêu cầu và các dữ kiện đã cho. Bài tập 4 thường yêu cầu học sinh:
Để giúp học sinh hiểu rõ hơn về cách giải bài tập này, chúng ta sẽ đi vào giải chi tiết từng bước. (Nội dung giải bài tập cụ thể sẽ được trình bày chi tiết tại đây, bao gồm các bước giải, công thức sử dụng và giải thích rõ ràng).
Để minh họa cho cách giải bài tập 4, chúng ta sẽ xem xét một ví dụ cụ thể. (Ví dụ minh họa sẽ được trình bày chi tiết, bao gồm đề bài, lời giải và giải thích).
Ngoài việc giải bài tập 4, chúng ta cũng cần mở rộng kiến thức về hàm số bậc nhất và hàm số bậc hai để có thể giải quyết các bài toán phức tạp hơn. Một số kiến thức mở rộng bao gồm:
Để củng cố kiến thức, bạn có thể làm thêm một số bài tập tương tự như bài tập 4 trang 74. (Danh sách các bài tập tương tự sẽ được liệt kê tại đây).
Khi giải bài tập về hàm số, bạn cần lưu ý một số điều sau:
Bài tập 4 trang 74 SGK Toán 9 tập 2 - Chân trời sáng tạo là một bài tập quan trọng giúp học sinh củng cố kiến thức về hàm số bậc nhất và hàm số bậc hai. Hy vọng rằng với hướng dẫn chi tiết này, bạn sẽ tự tin giải quyết bài tập và đạt kết quả tốt trong môn Toán 9.
SGK Toán 9 tập 2 - Chân trời sáng tạo
Sách bài tập Toán 9
Các trang web học Toán online uy tín
| Tiêu chí | Mô tả |
|---|---|
| Mục tiêu | Hiểu rõ cách giải bài tập 4 trang 74 SGK Toán 9 tập 2 |
| Đối tượng | Học sinh lớp 9 |
| Nội dung | Phân tích đề bài, lời giải chi tiết, ví dụ minh họa, mở rộng kiến thức |
| Giaitoan.edu.vn - Nơi học Toán 9 hiệu quả! | |