Giaitoan.edu.vn xin giới thiệu bộ giải đáp chi tiết các bài tập trang 111 SGK Toán 9 tập 2 - Chân trời sáng tạo. Chúng tôi hiểu rằng việc tự học đôi khi gặp nhiều khó khăn, đặc biệt là với những bài toán phức tạp.
Do đó, đội ngũ giáo viên giàu kinh nghiệm của chúng tôi đã biên soạn lời giải dễ hiểu, logic, giúp học sinh nắm vững kiến thức và rèn luyện kỹ năng giải toán.
Thực hiện các hoạt động 1, 2 và 3 đối với vòng quay là đường tròn ngoại tiếp lục giác đều.
Đề bài
Trả lời câu hỏi Thực hành trang 111 SGK Toán 9 Chân trời sáng tạo
Thực hiện các hoạt động 1, 2 và 3 đối với vòng quay là đường tròn ngoại tiếp lục giác đều.
Video hướng dẫn giải
Phương pháp giải - Xem chi tiết
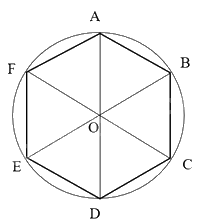
Hoạt động 1. Thực hiện vẽ hình lục giác đều trên đường tròn.
Hoạt động 2. Làm vòng quay may mắn bằng hình lục giác đều.
Hoạt động 3. Thực hiện quay vòng quay may mắn từ đó so sánh xác suất lí thuyết và xác suất thực nghiệm.
Lời giải chi tiết
Hoạt động 1:
Để vẽ lục giác đều, ta thực hiện các bước sau:
- Dùng compa vẽ đường tròn tâm O bán kính 5cm.
- Tính số đo của cung có dây là cạnh của lục giác đều, ta có $\frac{360{}^\circ }{6}=60{}^\circ $.
- Dùng thước đo góc để vẽ 6 góc ở tâm kề nhau $\widehat{AOB},\widehat{BOC},\widehat{COD},\widehat{DOE},\widehat{EOF},\widehat{FOA}$, mỗi góc có số đo bằng $60{}^\circ $. Các góc này chia đường tròn thành các cung có số đo bằng $60{}^\circ $.
- Nối các đầu mút của các cung này, ta có lục giác đều.
Hoạt động 2:
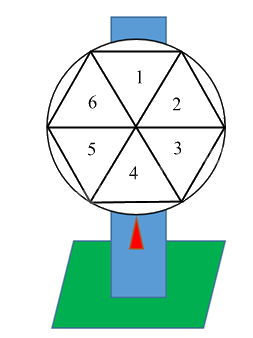
- Cắt hình đa giác đều vừa vẽ, dán lên một tấm bìa và cắt tấm bìa theo đường tròn ta được vòng quay.
- Đánh số thứ tự từ 1 đến 6 vào các phần trên vòng quay.
– Dùng bìa hộp cũ cắt hai hình chữ nhật làm thân và đế của giá quay.
– Dùng đinh ghim tâm vòng quay vào giá quay.
– Vẽ tam giác trên giá quay làm kim chỉ kết quả.
– Sản phẩm hoàn chỉnh là vòng quay trong hình.
Hoạt động 3:
Có 6 kết quả có thể xảy ra.
Xác suất lý thuyết để kim chỉ vào một số trên vòng quay là: $p\left( A \right)=\frac{1}{6}$
Ví dụ, ta có bảng xác suất thực nghiệm khi thực hiện quay trong 20 lần:
Giá trị | 1 | 2 | 3 | 4 | 5 | 6 |
Tần số | 3 | 1 | 4 | 5 | 3 | 4 |
Xác suất | $\frac{3}{20}=0,15$ | $\frac{1}{20}=0,05$ | $\frac{4}{20}=0,2$ | $\frac{5}{20}=0,25$ | $\frac{3}{20}=0,15$ | $\frac{4}{20}=0,2$ |
Như vậy, xác suất trong thực tế khác hoàn toàn xác suất lý thuyết, nguyên nhân là do các kết quả thu được là ngẫu nhiên.
Trang 111 SGK Toán 9 tập 2 - Chân trời sáng tạo tập trung vào việc ôn tập chương 4: Hệ phương trình bậc hai hai ẩn. Các bài tập trong trang này yêu cầu học sinh vận dụng kiến thức đã học để giải các hệ phương trình, tìm điều kiện để hệ phương trình có nghiệm duy nhất, vô nghiệm hoặc vô số nghiệm, và ứng dụng vào giải các bài toán thực tế.
Bài 1 yêu cầu học sinh giải các hệ phương trình bằng phương pháp thế. Phương pháp này dựa trên việc biểu diễn một ẩn theo ẩn còn lại từ một phương trình, sau đó thay thế biểu thức đó vào phương trình còn lại để tìm ra giá trị của ẩn còn lại. Ví dụ:
Bài 2 yêu cầu học sinh giải các hệ phương trình bằng phương pháp cộng đại số. Phương pháp này dựa trên việc cộng hoặc trừ các phương trình để loại bỏ một ẩn, sau đó tìm giá trị của ẩn còn lại. Ví dụ:
Bài 3 yêu cầu học sinh tìm điều kiện của tham số m để hệ phương trình có nghiệm duy nhất. Để hệ phương trình có nghiệm duy nhất, định thức của hệ phương trình phải khác 0. Định thức của hệ phương trình được tính bằng công thức:
D = a1b2 - a2b1, trong đó a1, a2, b1, b2 là các hệ số của hệ phương trình.
Ví dụ: Hệ phương trình mx + y = 1 và x + my = 1. Ta có D = m*m - 1*1 = m^2 - 1. Để hệ phương trình có nghiệm duy nhất, ta cần m^2 - 1 ≠ 0, tức là m ≠ ±1.
Bài 4 thường là các bài toán thực tế liên quan đến việc tìm hai số khi biết tổng và tích của chúng, hoặc các bài toán về vận tốc, thời gian, quãng đường. Để giải các bài toán này, học sinh cần đặt ẩn số, lập hệ phương trình dựa trên các dữ kiện của bài toán, và giải hệ phương trình để tìm ra giá trị của ẩn số.
Ví dụ: Một người đi xe máy từ A đến B với vận tốc 40km/h, sau đó quay trở lại A với vận tốc 30km/h. Thời gian cả đi lẫn về là 5 giờ. Tính quãng đường AB.
Giải: Gọi x là quãng đường AB (km). Thời gian đi từ A đến B là x/40 (giờ), thời gian đi từ B về A là x/30 (giờ). Ta có hệ phương trình:
Giải hệ phương trình, ta được x = 60. Vậy quãng đường AB là 60km.
Giaitoan.edu.vn hy vọng với lời giải chi tiết và dễ hiểu này, các em học sinh sẽ tự tin hơn trong việc giải các bài tập Toán 9 trang 111 SGK Chân trời sáng tạo. Chúc các em học tập tốt!