Chào mừng bạn đến với bài học lý thuyết Đường tròn Toán 9 Chân trời sáng tạo trên giaitoan.edu.vn. Bài học này sẽ cung cấp cho bạn những kiến thức cơ bản và quan trọng nhất về đường tròn, một trong những khái niệm nền tảng của hình học lớp 9.
Chúng tôi sẽ cùng nhau khám phá định nghĩa, các yếu tố của đường tròn, các tính chất quan trọng và các ứng dụng thực tế của nó. Mục tiêu của chúng ta là giúp bạn hiểu rõ lý thuyết và có thể áp dụng nó để giải quyết các bài tập một cách hiệu quả.
1. Khái niệm đường tròn Đường tròn tâm O bán kính R (R > 0), là hình gồm tất cả các điểm cách điểm O một khoảng bằng R, kí hiệu (O; R).
1. Khái niệm đường tròn
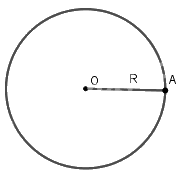
Đường tròn tâm O bán kính R (R > 0), là hình gồm tất cả các điểm cách điểm O một khoảng bằng R, kí hiệu (O; R). |
Khi không cần chú ý đến bán kính, đường tròn (O;R) còn được kí hiệu là (O).
Vị trí tương đối của điểm và đường tròn
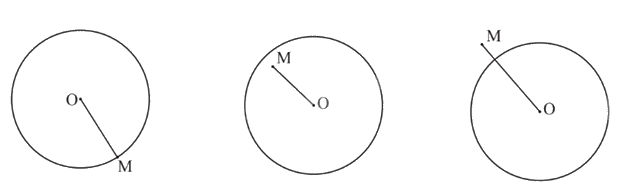
Cho đường tròn (O; R) và điểm M. Khi đó:
- Nếu OM = R thì điểm M nằm trên đường tròn hay M thuộc đường tròn;
- Nếu OM < R thì điểm M nằm trong đường tròn;
- Nếu OM > R thì điểm M nằm ngoài đường tròn.
2. Tính đối xứng của đường tròn
Đường tròn là hình có tâm đối xứng; tâm đối xứng là tâm của đường tròn. Đường tròn là hình có trục đối xứng. Mọi đường thẳng đi qua tâm của đường tròn đều là trục đối xứng của nó. |
Ví dụ:
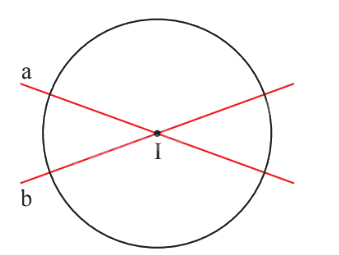
Hình tròn tâm I có:
I là tâm đối xứng;
Đường thẳng a, b là các trục đối xứng của hình tròn (I).
3. Đường kính và dây cung của đường tròn
Cho hai điểm C, D cùng thuộc một đường tròn. Đoạn thẳng CD gọi là dây cung hoặc dây. Đường kính AB là một dây đi qua tâm.
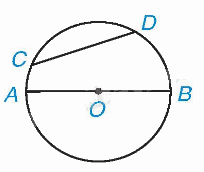
Quan hệ giữa dây và đường kính
Trong các dây của một đường tròn, đường kính là dây có độ dài lớn nhất. |
4. Vị trí tương đối của hai đường tròn
• Hai đường tròn không có điểm chung gọi là hai đường tròn không giao nhau. Hai đường tròn không giao nhau có thể ở ngoài nhau hoặc đường tròn này đựng đường tròn kia. • Hai đường tròn chỉ có một điểm chung gọi là hai đường tròn tiếp xúc nhau. Điểm chung đó gọi là tiếp điểm. Hai đường tròn tiếp xúc có thể tiếp xúc ngoài hoặc tiếp xúc trong. • Hai đường tròn có đúng hai điểm chung gọi là hai đường tròn cắt nhau. Hai điểm chung gọi là hai giao điểm. Đoạn thẳng nối hai điểm chung được gọi là dây chung. |
Chú ý: Nếu OO’ = 0 thì O trùng với O’. Hai đường tròn có tâm trùng nhau gọi là hai đường tròn đồng tâm.
Bảng tóm tắt vị trí tương đối của hai đường tròn phân biệt (O;R) và (O’; R’) với \(R \ge R'\)
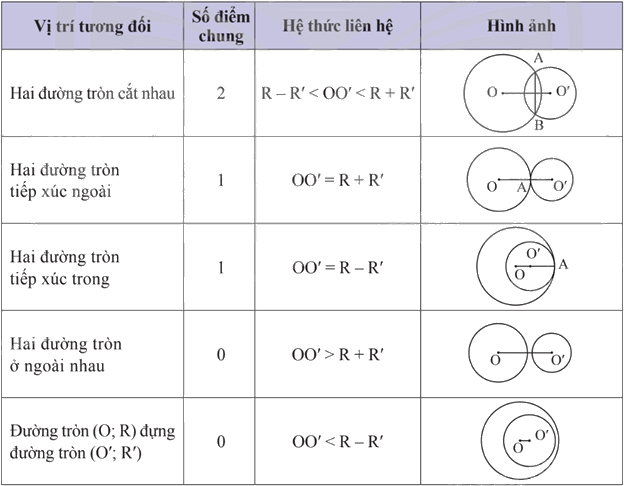
Ví dụ 1: Cho OO’ = 5cm, khi đó hai đường tròn (O;4cm) và (O’;3cm) cắt nhau vì:
4cm – 3cm = 1cm < 5cm < 7cm = 4cm + 3cm.
Ví dụ 2: Cho OO’ = 5cm, khi đó hai đường tròn (O;3cm) và (O’;2cm) tiếp xúc ngoài với nhau vì 5cm = 3cm + 2cm.
Cho OO’ = 3cm, khi đó hai đường tròn (O;8cm) và (O’;5cm) tiếp xúc trong với nhau vì 3cm = 8cm - 5cm.
Ví dụ 3: Cho đường tròn (O;3cm) và (O’;4cm) có \(OO' > 8cm\) thì \(OO' = 8cm > 3cm + 4cm = R + R'\) nên (O;3cm) và (O’;4cm) là hai đường tròn ngoài nhau.
Đường tròn là một trong những hình học cơ bản và quan trọng trong chương trình Toán 9, đặc biệt trong sách giáo khoa Chân trời sáng tạo. Việc nắm vững lý thuyết đường tròn không chỉ giúp học sinh giải quyết các bài toán hình học mà còn là nền tảng cho các kiến thức toán học nâng cao hơn.
Đường tròn là tập hợp tất cả các điểm nằm trên một mặt phẳng, cách đều một điểm cố định gọi là tâm của đường tròn. Khoảng cách từ tâm đến bất kỳ điểm nào trên đường tròn được gọi là bán kính (R) của đường tròn.
Đường tròn có tính chất đối xứng cao:
Có ba trường hợp vị trí tương đối giữa một đường thẳng và một đường tròn:
Trong một đường tròn:
Đây là hai khái niệm quan trọng liên quan đến đường tròn:
Mối quan hệ giữa góc ở tâm và góc nội tiếp cùng chắn một cung là: Góc ở tâm bằng hai lần góc nội tiếp cùng chắn một cung.
Lý thuyết đường tròn có nhiều ứng dụng trong thực tế, ví dụ:
Để củng cố kiến thức về lý thuyết đường tròn, bạn có thể thực hành giải các bài tập sau:
Hy vọng bài học lý thuyết Đường tròn Toán 9 Chân trời sáng tạo này sẽ giúp bạn hiểu rõ hơn về kiến thức này và tự tin giải các bài tập liên quan. Chúc bạn học tập tốt!