Chào mừng các em học sinh đến với chuyên mục giải bài tập Toán 9 tập 2 của giaitoan.edu.vn. Ở bài viết này, chúng tôi sẽ cung cấp lời giải chi tiết và dễ hiểu cho các bài tập trong mục 1 trang 84 và 85 sách giáo khoa Toán 9 tập 2, chương trình Chân trời sáng tạo.
Mục tiêu của chúng tôi là giúp các em nắm vững kiến thức, rèn luyện kỹ năng giải toán và tự tin hơn trong các kỳ thi sắp tới.
Cho tấm bìa có dạng hình chữ nhật AA’O’O (Hình 1a). Khi quay tấm bìa một vòng quanh OO’ cố định thì hình tạo ra giống với đồ vật quen thuộc nào?
Video hướng dẫn giải
Trả lời câu hỏi Thực hành 2 trang 85 SGK Toán 9 Chân trời sáng tạo
Tạo lập chiếc hộp dạng hình trụ có chiều cao 10 cm, bán kính đáy 3 cm theo hướng dẫn sau:
Bước 1: cắt một tấm bìa hình chữ nhật có cạnh 10 cm và cạnh 6\(\pi \)cm (\( \approx \) 19 cm) (Hình 5a).
Bước 2: ghép hai cạnh 10 cm của tấm bìa lại với nhau sao cho hai cạnh 6\(\pi \)cm được uốn cong tạo thành hai đường tròn như Hình 5b.
Bước 3: Cắt hai tấm bìa hình tròn bán kính 3 cm rồi dán vào hai đường tròn vừa tạo thành ở Bước 2, ta được chiếc hộp như yêu cầu (Hình 5c).
Phương pháp giải:
Đọc kĩ dữ kiện đề bài và làm theo.
Lời giải chi tiết:
Lấy giấy làm thủ công tương tự các bước như ở trên.
Video hướng dẫn giải
Trả lời câu hỏi Thực hành 1 trang 85 SGK Toán 9 Chân trời sáng tạo
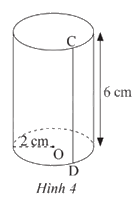
Quan sát và cho biết đường sinh, độ dài bán kính đáy và chiều cao của hình trụ trong Hình 4.
Phương pháp giải:
Dựa vào: Khi quay hình chữ nhật AA’OO’ một vòng quanh cạnh OO’ cố định ta được một hình trụ.
+ Cạnh OA, O’A’ quét thành hai hình tròn có cùng bán kính gọi hai đáy của hình trụ; bán kính của đáy gọi là bán kính đáy của hình trụ.
+ Cạnh AA’ quét thành mặt xung quanh của hình trụ, mỗi vị trí của AA’ được coi là một đường sinh.
+ Độ dài OO’ gọi là chiều cao của hình cao. Các đường sinh có độ dài bằng nhau và bằng chiều cao hình trụ.
Lời giải chi tiết:
Đường sinh của hình trụ là CD.
Độ dài bán kính đáy là: 2 cm.
Chiều cao hình trụ là: 6 cm.
Video hướng dẫn giải
Trả lời câu hỏi Hoạt động 1 trang 84 SGK Toán 9 Chân trời sáng tạo
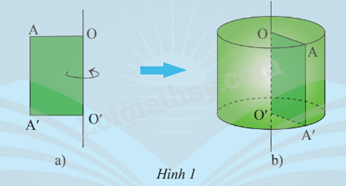
Cho tấm bìa có dạng hình chữ nhật AA’O’O (Hình 1a). Khi quay tấm bìa một vòng quanh OO’ cố định thì hình tạo ra giống với đồ vật quen thuộc nào?
Phương pháp giải:
Tìm các vật thực tế.
Lời giải chi tiết:
Khi quay tấm bìa một vòng quanh cạnh OO’ cố định thì tạo ra giống với hộp sữa đặc, hộp đựng cầu lông,...
Video hướng dẫn giải
Trả lời câu hỏi Hoạt động 1 trang 84 SGK Toán 9 Chân trời sáng tạo
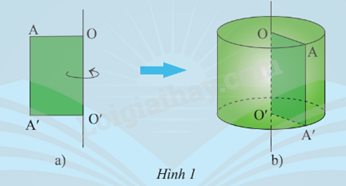
Cho tấm bìa có dạng hình chữ nhật AA’O’O (Hình 1a). Khi quay tấm bìa một vòng quanh OO’ cố định thì hình tạo ra giống với đồ vật quen thuộc nào?
Phương pháp giải:
Tìm các vật thực tế.
Lời giải chi tiết:
Khi quay tấm bìa một vòng quanh cạnh OO’ cố định thì tạo ra giống với hộp sữa đặc, hộp đựng cầu lông,...
Video hướng dẫn giải
Trả lời câu hỏi Thực hành 1 trang 85 SGK Toán 9 Chân trời sáng tạo
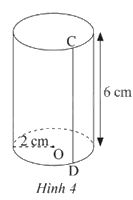
Quan sát và cho biết đường sinh, độ dài bán kính đáy và chiều cao của hình trụ trong Hình 4.
Phương pháp giải:
Dựa vào: Khi quay hình chữ nhật AA’OO’ một vòng quanh cạnh OO’ cố định ta được một hình trụ.
+ Cạnh OA, O’A’ quét thành hai hình tròn có cùng bán kính gọi hai đáy của hình trụ; bán kính của đáy gọi là bán kính đáy của hình trụ.
+ Cạnh AA’ quét thành mặt xung quanh của hình trụ, mỗi vị trí của AA’ được coi là một đường sinh.
+ Độ dài OO’ gọi là chiều cao của hình cao. Các đường sinh có độ dài bằng nhau và bằng chiều cao hình trụ.
Lời giải chi tiết:
Đường sinh của hình trụ là CD.
Độ dài bán kính đáy là: 2 cm.
Chiều cao hình trụ là: 6 cm.
Video hướng dẫn giải
Trả lời câu hỏi Thực hành 2 trang 85 SGK Toán 9 Chân trời sáng tạo
Tạo lập chiếc hộp dạng hình trụ có chiều cao 10 cm, bán kính đáy 3 cm theo hướng dẫn sau:
Bước 1: cắt một tấm bìa hình chữ nhật có cạnh 10 cm và cạnh 6\(\pi \)cm (\( \approx \) 19 cm) (Hình 5a).
Bước 2: ghép hai cạnh 10 cm của tấm bìa lại với nhau sao cho hai cạnh 6\(\pi \)cm được uốn cong tạo thành hai đường tròn như Hình 5b.
Bước 3: Cắt hai tấm bìa hình tròn bán kính 3 cm rồi dán vào hai đường tròn vừa tạo thành ở Bước 2, ta được chiếc hộp như yêu cầu (Hình 5c).
Phương pháp giải:
Đọc kĩ dữ kiện đề bài và làm theo.
Lời giải chi tiết:
Lấy giấy làm thủ công tương tự các bước như ở trên.
Mục 1 trang 84, 85 SGK Toán 9 tập 2 - Chân trời sáng tạo tập trung vào việc ôn tập và hệ thống hóa kiến thức về hàm số bậc nhất. Các bài tập trong mục này yêu cầu học sinh vận dụng các kiến thức đã học để giải quyết các bài toán thực tế, đồng thời rèn luyện kỹ năng tư duy logic và khả năng giải quyết vấn đề.
Bài 1 yêu cầu học sinh nhắc lại các khái niệm cơ bản về hàm số bậc nhất, bao gồm định nghĩa, dạng tổng quát, hệ số góc, và cách xác định hàm số.
Bài 2 yêu cầu học sinh xác định hàm số bậc nhất khi biết đồ thị của nó. Để làm được bài này, học sinh cần xác định được hai điểm thuộc đồ thị và sử dụng công thức tính hệ số góc.
Ví dụ: Cho đồ thị của hàm số đi qua hai điểm A(1; 2) và B(2; 4). Hãy xác định hàm số.
Bài 3 yêu cầu học sinh vẽ đồ thị của hàm số bậc nhất. Để vẽ đồ thị, học sinh cần xác định được ít nhất hai điểm thuộc đồ thị và nối chúng lại bằng một đường thẳng.
Ví dụ: Vẽ đồ thị của hàm số y = -x + 3
Khi giải các bài tập về hàm số bậc nhất, học sinh cần lưu ý những điều sau:
Hàm số bậc nhất có nhiều ứng dụng trong thực tế, ví dụ như:
Hy vọng với lời giải chi tiết và những lưu ý trên, các em học sinh sẽ tự tin hơn khi giải các bài tập trong mục 1 trang 84, 85 SGK Toán 9 tập 2 - Chân trời sáng tạo. Chúc các em học tập tốt!