Chào mừng bạn đến với bài học về lý thuyết Hình quạt tròn và hình vành khuyên trong chương trình Toán 9 Chân trời sáng tạo. Bài học này sẽ cung cấp cho bạn những kiến thức cơ bản và quan trọng nhất về hai hình này.
Chúng ta sẽ cùng nhau tìm hiểu định nghĩa, công thức tính diện tích, độ dài cung và các bài tập ứng dụng thực tế. Mục tiêu là giúp bạn hiểu rõ bản chất và có thể giải quyết các bài toán liên quan một cách hiệu quả.
1. Độ dài cung tròn Công thức tính chu vi đường tròn Công thức tính độ dài C của đường tròn (O; R), đường kính d = 2R là: \(C = \pi d = 2\pi R\)
1. Độ dài cung tròn
Công thức tính chu vi đường tròn
Công thức tính độ dài C của đường tròn (O; R), đường kính d = 2R là:
\(C = \pi d = 2\pi R\)
Công thức tính độ dài cung tròn
Trên đường tròn bán kính R, độ dài l của một cung có số đo \({n^0}\) được tính theo công thức: \(l = \frac{{\pi Rn}}{{180}}\). |
Ví dụ:
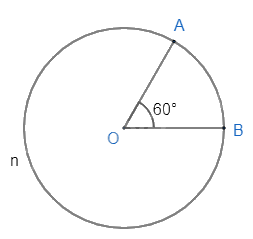
Đường tròn (O; 2cm), \(\widehat {AOB} = {60^0}\).
- Cung nhỏ AB bị chắn bởi góc ở tâm AOB.
Do đó sđ$\overset\frown{AB}=\widehat{AOB}={{60}^{0}}$
Độ dài \({l_1}\) của cung AB là:
\({l_1} = \frac{n}{{180}}\pi R = \frac{{60}}{{180}}\pi .2 = \frac{{2\pi }}{3} \approx 2,1\left( {cm} \right)\)
Cung lớn AnB có số đo là:
sđ$\overset\frown{AmN}={{360}^{o}}-{{60}^{0}}={{300}^{0}}$.
Độ dài \({l_2}\) của cung AnB là:
\({l_2} = \frac{{300}}{{180}}\pi .2 = \frac{{10}}{3}\pi \approx 10,5\left( {cm} \right)\)
2. Hình quạt tròn
Khái niệm hình quạt tròn
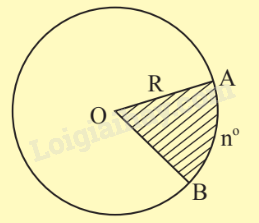
Hình quạt tròn là một phần hình tròn giới hạn bởi một cung tròn và hai bán kính đi qua hai mút của cung đó. |
Diện tích hình quạt tròn
Diện tích hình quạt tròn bán kính R ứng với cung \({n^o}\): \(S = \frac{{\pi {R^2}n}}{{360}}\) |
Ví dụ: Diện tích hình quạt tròn có độ dài tương ứng với nó là \(l = 4\pi \)cm, bán kính là R = 5cm là:
\({S_q} = \frac{{l.R}}{2} = \frac{{4\pi .5}}{2} = 10\pi \left( {c{m^2}} \right)\)
Khái niệm hình vành khuyên
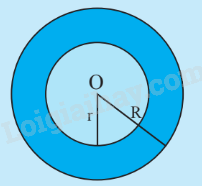
Cho hai đường tròn đồng tâm \(\left( {O;R} \right)\) và \(\left( {O;r} \right)\) với \(R > r\). Hình vành khuyên là phần mặt phẳng giới hạn bởi hai đường tròn (O;r) và (O;R) được tính bởi công thức: \(S = \pi \left( {{R^2} - {r^2}} \right)\). |
Diện tích hình vành khuyên
Diện tích \({S_v}\) của hình vành khuyên tạo bởi hai đường tròn đồng tâm và có bán kính R và r: \({S_v} = \pi \left( {{R^2} - {r^2}} \right)\) (với R > r) |
Ví dụ: Diện tích hình vành khuyên nằm giữa hai đường tròn đồng tâm có bán kính là 3m và 5m là:
\({S_v} = \pi \left( {{5^2} - {3^2}} \right) = 16\pi \left( {{m^2}} \right)\)
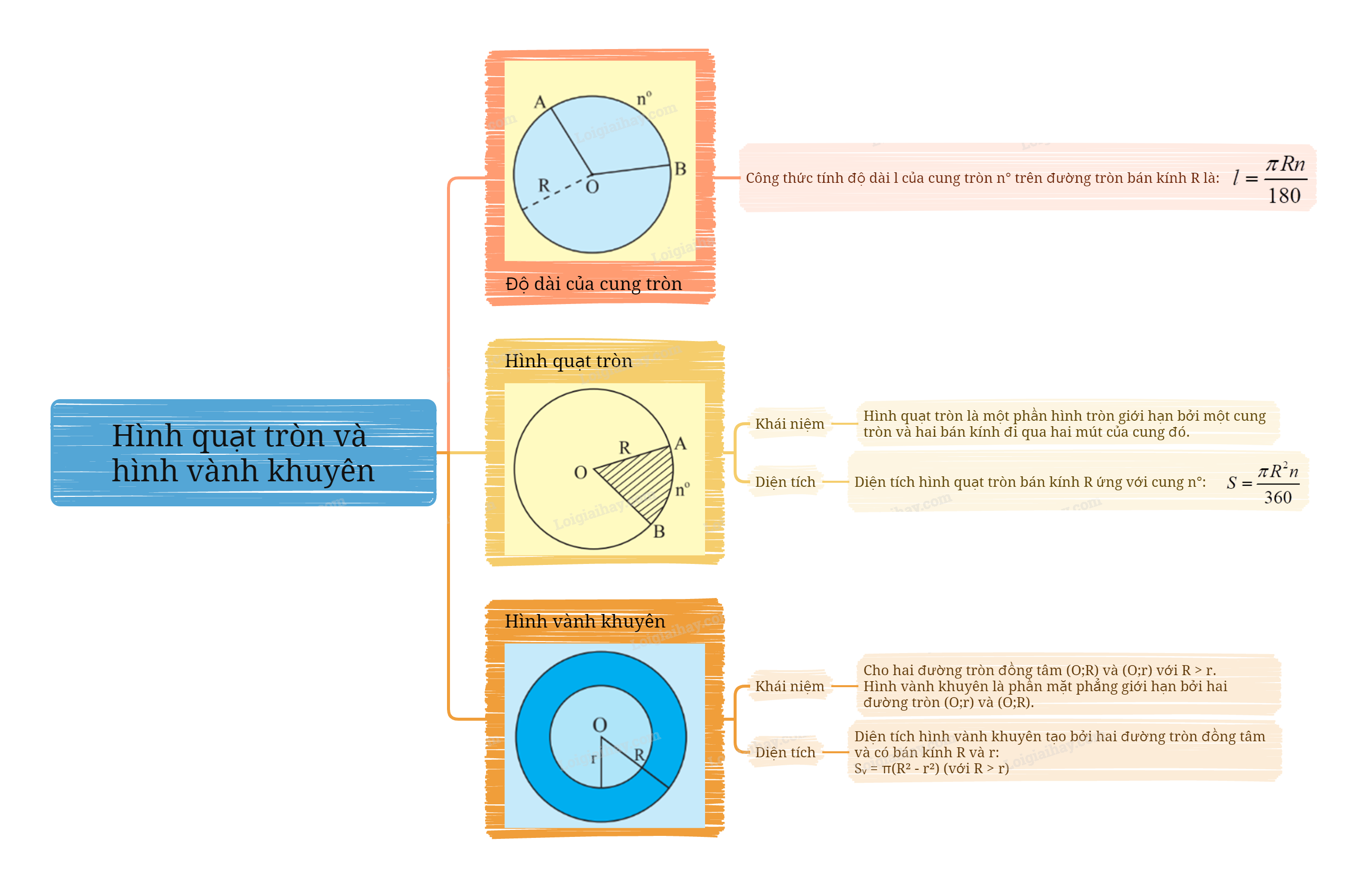
Trong chương trình Toán 9 Chân trời sáng tạo, kiến thức về hình học đóng vai trò quan trọng, và hình quạt tròn cùng hình vành khuyên là những khái niệm cần được nắm vững. Bài viết này sẽ cung cấp một cách chi tiết và dễ hiểu về lý thuyết, công thức và ứng dụng của hai hình này.
1. Định nghĩa: Hình quạt tròn là một phần của hình tròn được giới hạn bởi hai bán kính và một cung tròn.
2. Các yếu tố của hình quạt tròn:
3. Công thức tính độ dài cung tròn:
Độ dài cung tròn (l) được tính bằng công thức: l = πr * (α/180°), trong đó:
4. Công thức tính diện tích hình quạt tròn:
Diện tích hình quạt tròn (S) được tính bằng công thức: S = πr² * (α/360°), trong đó:
1. Định nghĩa: Hình vành khuyên là phần diện tích nằm giữa hai đường tròn đồng tâm có bán kính khác nhau.
2. Các yếu tố của hình vành khuyên:
3. Công thức tính diện tích hình vành khuyên:
Diện tích hình vành khuyên (S) được tính bằng công thức: S = πR² - πr² = π(R² - r²), trong đó:
Bài 1: Một hình quạt tròn có bán kính 5cm và góc ở tâm 72°. Tính độ dài cung tròn và diện tích hình quạt tròn.
Giải:
Độ dài cung tròn: l = π * 5 * (72/180) = 2π (cm)
Diện tích hình quạt tròn: S = π * 5² * (72/360) = 5π (cm²)
Bài 2: Một hình vành khuyên có bán kính lớn 8cm và bán kính nhỏ 5cm. Tính diện tích hình vành khuyên.
Giải:
Diện tích hình vành khuyên: S = π * (8² - 5²) = π * (64 - 25) = 39π (cm²)
Khi tính toán diện tích và độ dài cung tròn, cần chú ý đến đơn vị đo lường. Đảm bảo rằng tất cả các giá trị đều được biểu diễn trong cùng một đơn vị.
Góc ở tâm có thể được biểu diễn bằng độ hoặc radian. Khi sử dụng công thức, cần đảm bảo rằng góc ở tâm được biểu diễn đúng đơn vị.
Hi vọng rằng bài viết này đã cung cấp cho bạn những kiến thức cơ bản và quan trọng về lý thuyết Hình quạt tròn và hình vành khuyên Toán 9 Chân trời sáng tạo. Việc nắm vững những kiến thức này sẽ giúp bạn giải quyết các bài toán một cách dễ dàng và hiệu quả hơn. Chúc bạn học tập tốt!