Chào mừng các em học sinh đến với chuyên mục giải bài tập Toán 9 tập 1 của giaitoan.edu.vn. Chúng tôi xin giới thiệu lời giải chi tiết và dễ hiểu cho mục 2 trang 91, 92, 93 sách giáo khoa Toán 9 tập 1 - Chân trời sáng tạo.
Mục tiêu của chúng tôi là giúp các em nắm vững kiến thức, rèn luyện kỹ năng giải toán và đạt kết quả tốt nhất trong học tập.
Vẽ vào vở đường tròn (O) và hai điểm A, B nằm trên (O). Dùng bút chì khác màu tô hai phần của đường tròn được phân chia bởi hai điểm A và B.
Video hướng dẫn giải
Trả lời câu hỏi Hoạt động 3 trang 91SGK Toán 9 Chân trời sáng tạo
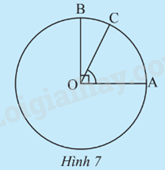
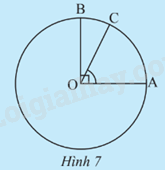
Cho OA và OB là hai bán kính vuông góc với nhau của đường tròn (O), C là điểm trên cung nhỏ AB (Hình 7). Ta coi số đo của một cung nhỏ là số đo của góc ở tâm chắn cung đó.
a) Xác định số đo cung AB.
b) So sánh số đo của hai cung \(\overset\frown{AC}\) và \(\overset\frown{AB}\)
Phương pháp giải:
Nhìn hình vẽ xác định số đo \(\overset\frown{AB}=\widehat{AOB}\) và \(\overset\frown{AC}\); \(\overset\frown{AB}\) .
Lời giải chi tiết:
a) Số đo cung AB bằng \(\widehat {AOB} = {90^o}\).
b) Ta có \(\overset\frown{AC}\) < \(\overset\frown{AB}\).
Video hướng dẫn giải
Trả lời câu hỏi Hoạt động 2 trang 91SGK Toán 9 Chân trời sáng tạo
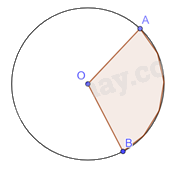
Vẽ vào vở đường tròn (O) và hai điểm A, B nằm trên (O). Dùng bút chì khác màu tô hai phần của đường tròn được phân chia bởi hai điểm A và B.
Phương pháp giải:
Đọc dữ liệu đề bài để vẽ hình.
Lời giải chi tiết:
Video hướng dẫn giải
Trả lời câu hỏi Thực hành 2 trang 92 SGK Toán 9 Chân trời sáng tạo
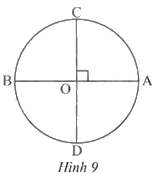
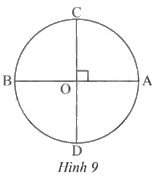
Cho đường tròn (O) có hai đường kính AB và CD vuông góc với nhau (Hình 9). Xác định số đo của các cung \(\overset\frown{AB}\),\(\overset\frown{AC}\) và \(\overset\frown{AD}\).
Phương pháp giải:
Dựa vào định nghĩa: Số đo cung nhỏ bằng số đo của góc ở tâm chắc cung đó và số đo của cung nửa đường tròn bằng 180o
Lời giải chi tiết:
Trong Hình 9, ta có cung \(\overset\frown{AB}\) chắn nửa đường tròn nên sđ \(\overset\frown{AB}\) = 180o
Cung \(\overset\frown{AC}\) bị chắn bởi góc ở tâm \(\widehat {COA}\) có số đo bằng 90o , suy ra sđ \(\overset\frown{AC}\) = 90o
Vì \(AB \bot CD\) tại O nên \(\widehat {AOD} = {90^o}\), cung \(\overset\frown{AD}\) bị chắn bởi góc ở tâm \(\widehat {AOD}\) suy ra sđ \(\overset\frown{AD}\) = 90o.
Video hướng dẫn giải
Trả lời câu hỏi Vận dụng 3 trang 93 SGK Toán 9 Chân trời sáng tạo
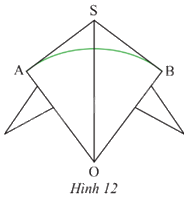
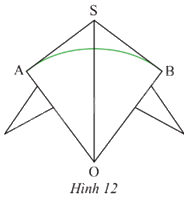
Bạn Hùng làm một cái diều với thân diều là hình tứ giác S.AOB sao cho OS là đường phân giác của \(\widehat {AOB}\) và \(\widehat {ASB} = {106^o}\). Thanh tre màu xanh lá được uốn cong thành cung AB của đường tròn tâm O và SA, SB là hai tiếp tuyến của (O) (Hình 12). Tính số đo của \(\overset\frown{AB}\).
Phương pháp giải:
- Dựa vào tính chất của tiếp tuyến và tổng các góc của tứ giác bằng 360o
- Dựa vào định nghĩa: Số đo cung nhỏ bằng số đo của góc ở tâm chắc cung đó.
Lời giải chi tiết:
Ta có SA, SB là hai tiếp tuyến của (O) nên OA \( \bot \) SA hay \(\widehat {OAS} = {90^o}\) và OB \( \bot \) SB hay \(\widehat {OBS} = {90^o}\).
Xét tứ giác SAOB có \(\widehat {ASB} + \widehat {OAS} + \widehat {AOB} + \widehat {OSB} = {360^o}\)
Suy ra \(\widehat {AOB} = {360^o} - \widehat {ASB} - \widehat {OAS} - \widehat {OSB} = {360^o} - {106^o} - {90^o} - {90^o} = {74^o}\)
Ta có sđ\(\overset\frown{AB}\) bị chắn bởi góc ở tâm \(\widehat {AOB}\) có số đo bằng 74o suy ra sđ\(\overset\frown{AB}\) = 74o .
Video hướng dẫn giải
Trả lời câu hỏi Hoạt động 4 trang 92 SGK Toán 9 Chân trời sáng tạo
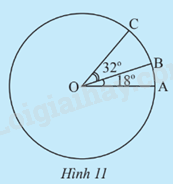
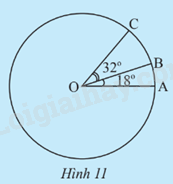
Trên đường tròn (O), vẽ hai cung nhỏ \(\overset\frown{AB}\); \(\overset\frown{BC}\) sao cho \(\widehat {AOB} = {18^o};\widehat {BOC} = {32^o}\) và tia OB ở giữa hai tia OA, OC (Hình 11). Tính số đo của các cung \(\overset\frown{AB}\); \(\overset\frown{BC}\); \(\overset\frown{AC}\).
Phương pháp giải:
Dựa vào định nghĩa: Số đo cung nhỏ bằng số đo của góc ở tâm chắc cung đó.
Lời giải chi tiết:
Trong Hình 11, ta có cung \(\overset\frown{AB}\) bị chắn bởi góc ở tâm \(\widehat{AOB}\)có số đo bằng 18o , suy ra sđ \(\overset\frown{AB}\)= 18o
Ta có cung \(\overset\frown{BC}\) bị chắn bởi góc ở tâm \(\widehat{BOC}\)có số đo bằng 32o , suy ra sđ \(\overset\frown{BC}\)= 32o
Ta có cung \(\overset\frown{AC}\) bị chắn bởi góc ở tâm \(\widehat{AOC}\)có số đo bằng 32o + 18 o = 50 o, suy ra sđ \(\overset\frown{AC}\)= 50o
Video hướng dẫn giải
Trả lời câu hỏi Thực hành 3 trang 93 SGK Toán 9 Chân trời sáng tạo
Trên cung AB có số đo 90o của đường tròn (O), lấy điểm M sao cho cung AM có số đo 15o. Tính số đo của cung MB.
Phương pháp giải:
- Đọc dữ kiện đề bài để vẽ hình.
- Dựa vào: Trên đường tròn (O), cho M là một điểm nằm trên cung AB. Ta nói điểm M chia cung AB thành hai cung \(\overset\frown{AM}\) và \(\overset\frown{MB}\) suy ra sđ\(\overset\frown{AB}\) = sđ\(\overset\frown{AM}\) + sđ\(\overset\frown{MB}\).
Lời giải chi tiết:
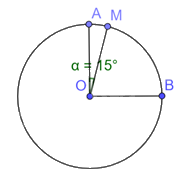
Ta có sđ \(\overset\frown{MB}\) = sđ \(\overset\frown{AB}\) - sđ \(\overset\frown{AM}\) = \({{90}^{o}}-{{15}^{o}}={{75}^{o}}\).
Video hướng dẫn giải
Trả lời câu hỏi Vận dụng 2 trang 92SGK Toán 9 Chân trời sáng tạo
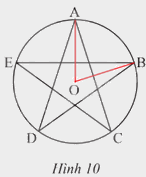
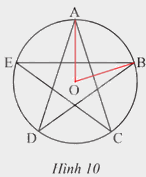
Xác định số đo cung AB trong hình ngôi sao năm cánh (Hình 10).
Phương pháp giải:
Dựa vào định nghĩa: góc có đỉnh trùng tâm đường tròn là góc ở tâm và tổng góc trong đường tròn bằng 360o
Lời giải chi tiết:
Ta có hình ngôi sao năm cánh có 5 góc ở tâm bằng nhau vậy mỗi góc là \(\frac{{{{360}^o}}}{5} = {72^o}\) hay sđ \(\overset\frown{AB}\) = 72o.
Video hướng dẫn giải
Trả lời câu hỏi Hoạt động 2 trang 91SGK Toán 9 Chân trời sáng tạo
Vẽ vào vở đường tròn (O) và hai điểm A, B nằm trên (O). Dùng bút chì khác màu tô hai phần của đường tròn được phân chia bởi hai điểm A và B.
Phương pháp giải:
Đọc dữ liệu đề bài để vẽ hình.
Lời giải chi tiết:
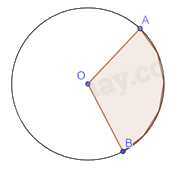
Video hướng dẫn giải
Trả lời câu hỏi Hoạt động 3 trang 91SGK Toán 9 Chân trời sáng tạo
Cho OA và OB là hai bán kính vuông góc với nhau của đường tròn (O), C là điểm trên cung nhỏ AB (Hình 7). Ta coi số đo của một cung nhỏ là số đo của góc ở tâm chắn cung đó.
a) Xác định số đo cung AB.
b) So sánh số đo của hai cung \(\overset\frown{AC}\) và \(\overset\frown{AB}\)
Phương pháp giải:
Nhìn hình vẽ xác định số đo \(\overset\frown{AB}=\widehat{AOB}\) và \(\overset\frown{AC}\); \(\overset\frown{AB}\) .
Lời giải chi tiết:
a) Số đo cung AB bằng \(\widehat {AOB} = {90^o}\).
b) Ta có \(\overset\frown{AC}\) < \(\overset\frown{AB}\).
Video hướng dẫn giải
Trả lời câu hỏi Thực hành 2 trang 92 SGK Toán 9 Chân trời sáng tạo
Cho đường tròn (O) có hai đường kính AB và CD vuông góc với nhau (Hình 9). Xác định số đo của các cung \(\overset\frown{AB}\),\(\overset\frown{AC}\) và \(\overset\frown{AD}\).
Phương pháp giải:
Dựa vào định nghĩa: Số đo cung nhỏ bằng số đo của góc ở tâm chắc cung đó và số đo của cung nửa đường tròn bằng 180o
Lời giải chi tiết:
Trong Hình 9, ta có cung \(\overset\frown{AB}\) chắn nửa đường tròn nên sđ \(\overset\frown{AB}\) = 180o
Cung \(\overset\frown{AC}\) bị chắn bởi góc ở tâm \(\widehat {COA}\) có số đo bằng 90o , suy ra sđ \(\overset\frown{AC}\) = 90o
Vì \(AB \bot CD\) tại O nên \(\widehat {AOD} = {90^o}\), cung \(\overset\frown{AD}\) bị chắn bởi góc ở tâm \(\widehat {AOD}\) suy ra sđ \(\overset\frown{AD}\) = 90o.
Video hướng dẫn giải
Trả lời câu hỏi Vận dụng 2 trang 92SGK Toán 9 Chân trời sáng tạo
Xác định số đo cung AB trong hình ngôi sao năm cánh (Hình 10).
Phương pháp giải:
Dựa vào định nghĩa: góc có đỉnh trùng tâm đường tròn là góc ở tâm và tổng góc trong đường tròn bằng 360o
Lời giải chi tiết:
Ta có hình ngôi sao năm cánh có 5 góc ở tâm bằng nhau vậy mỗi góc là \(\frac{{{{360}^o}}}{5} = {72^o}\) hay sđ \(\overset\frown{AB}\) = 72o.
Video hướng dẫn giải
Trả lời câu hỏi Hoạt động 4 trang 92 SGK Toán 9 Chân trời sáng tạo
Trên đường tròn (O), vẽ hai cung nhỏ \(\overset\frown{AB}\); \(\overset\frown{BC}\) sao cho \(\widehat {AOB} = {18^o};\widehat {BOC} = {32^o}\) và tia OB ở giữa hai tia OA, OC (Hình 11). Tính số đo của các cung \(\overset\frown{AB}\); \(\overset\frown{BC}\); \(\overset\frown{AC}\).
Phương pháp giải:
Dựa vào định nghĩa: Số đo cung nhỏ bằng số đo của góc ở tâm chắc cung đó.
Lời giải chi tiết:
Trong Hình 11, ta có cung \(\overset\frown{AB}\) bị chắn bởi góc ở tâm \(\widehat{AOB}\)có số đo bằng 18o , suy ra sđ \(\overset\frown{AB}\)= 18o
Ta có cung \(\overset\frown{BC}\) bị chắn bởi góc ở tâm \(\widehat{BOC}\)có số đo bằng 32o , suy ra sđ \(\overset\frown{BC}\)= 32o
Ta có cung \(\overset\frown{AC}\) bị chắn bởi góc ở tâm \(\widehat{AOC}\)có số đo bằng 32o + 18 o = 50 o, suy ra sđ \(\overset\frown{AC}\)= 50o
Video hướng dẫn giải
Trả lời câu hỏi Thực hành 3 trang 93 SGK Toán 9 Chân trời sáng tạo
Trên cung AB có số đo 90o của đường tròn (O), lấy điểm M sao cho cung AM có số đo 15o. Tính số đo của cung MB.
Phương pháp giải:
- Đọc dữ kiện đề bài để vẽ hình.
- Dựa vào: Trên đường tròn (O), cho M là một điểm nằm trên cung AB. Ta nói điểm M chia cung AB thành hai cung \(\overset\frown{AM}\) và \(\overset\frown{MB}\) suy ra sđ\(\overset\frown{AB}\) = sđ\(\overset\frown{AM}\) + sđ\(\overset\frown{MB}\).
Lời giải chi tiết:
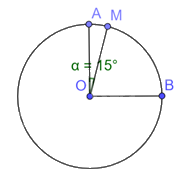
Ta có sđ \(\overset\frown{MB}\) = sđ \(\overset\frown{AB}\) - sđ \(\overset\frown{AM}\) = \({{90}^{o}}-{{15}^{o}}={{75}^{o}}\).
Video hướng dẫn giải
Trả lời câu hỏi Vận dụng 3 trang 93 SGK Toán 9 Chân trời sáng tạo
Bạn Hùng làm một cái diều với thân diều là hình tứ giác S.AOB sao cho OS là đường phân giác của \(\widehat {AOB}\) và \(\widehat {ASB} = {106^o}\). Thanh tre màu xanh lá được uốn cong thành cung AB của đường tròn tâm O và SA, SB là hai tiếp tuyến của (O) (Hình 12). Tính số đo của \(\overset\frown{AB}\).
Phương pháp giải:
- Dựa vào tính chất của tiếp tuyến và tổng các góc của tứ giác bằng 360o
- Dựa vào định nghĩa: Số đo cung nhỏ bằng số đo của góc ở tâm chắc cung đó.
Lời giải chi tiết:
Ta có SA, SB là hai tiếp tuyến của (O) nên OA \( \bot \) SA hay \(\widehat {OAS} = {90^o}\) và OB \( \bot \) SB hay \(\widehat {OBS} = {90^o}\).
Xét tứ giác SAOB có \(\widehat {ASB} + \widehat {OAS} + \widehat {AOB} + \widehat {OSB} = {360^o}\)
Suy ra \(\widehat {AOB} = {360^o} - \widehat {ASB} - \widehat {OAS} - \widehat {OSB} = {360^o} - {106^o} - {90^o} - {90^o} = {74^o}\)
Ta có sđ\(\overset\frown{AB}\) bị chắn bởi góc ở tâm \(\widehat {AOB}\) có số đo bằng 74o suy ra sđ\(\overset\frown{AB}\) = 74o .
Mục 2 của chương trình Toán 9 tập 1 - Chân trời sáng tạo tập trung vào việc ôn tập và hệ thống hóa kiến thức về hàm số bậc nhất. Các bài tập trong mục này yêu cầu học sinh vận dụng các kiến thức đã học để giải quyết các bài toán thực tế, đồng thời rèn luyện kỹ năng tư duy logic và khả năng giải quyết vấn đề.
Bài tập này yêu cầu học sinh nhắc lại các khái niệm cơ bản về hàm số bậc nhất, bao gồm định nghĩa, dạng tổng quát, hệ số góc, và cách xác định hàm số.
Bài tập này yêu cầu học sinh vẽ đồ thị của hàm số bậc nhất và xác định các yếu tố quan trọng trên đồ thị, như giao điểm với các trục tọa độ.
Bài tập này yêu cầu học sinh vận dụng kiến thức về hàm số bậc nhất để giải quyết các bài toán thực tế, như tính quãng đường đi được, tính tiền lương, hoặc tính lợi nhuận.
Ví dụ: Một người đi xe đạp với vận tốc 15 km/h. Hỏi sau 2 giờ người đó đi được quãng đường bao nhiêu?
Giải: Gọi s là quãng đường người đó đi được sau 2 giờ. Ta có s = 15 * 2 = 30 km.
Dưới đây là lời giải chi tiết cho từng bài tập trong mục 2 trang 91, 92, 93 SGK Toán 9 tập 1 - Chân trời sáng tạo:
| Bài tập | Lời giải |
|---|---|
| Bài 1.1 | ... (Lời giải chi tiết bài 1.1) ... |
| Bài 1.2 | ... (Lời giải chi tiết bài 1.2) ... |
| Bài 1.3 | ... (Lời giải chi tiết bài 1.3) ... |
| Bài 2.1 | ... (Lời giải chi tiết bài 2.1) ... |
| Bài 2.2 | ... (Lời giải chi tiết bài 2.2) ... |
Hy vọng với lời giải chi tiết và dễ hiểu này, các em học sinh sẽ tự tin hơn khi giải các bài tập trong mục 2 trang 91, 92, 93 SGK Toán 9 tập 1 - Chân trời sáng tạo. Chúc các em học tập tốt!