Chào mừng các em học sinh đến với chuyên mục giải bài tập Toán 9 tập 1 của giaitoan.edu.vn. Ở bài viết này, chúng tôi sẽ cung cấp lời giải chi tiết và dễ hiểu cho các bài tập trong mục 2 trang 54, 55, 56 sách giáo khoa Toán 9 tập 1 - Chân trời sáng tạo.
Mục tiêu của chúng tôi là giúp các em nắm vững kiến thức, rèn luyện kỹ năng giải toán và đạt kết quả tốt nhất trong học tập.
Hình vuông ABCD được chia thành hai hình vuông và hai hình chữ nhật như Hình 3. a) Tính độ dài đường chéo của hai hình vuông AMIN và CEIF. b) Tính độ dài đường chéo của hai hình vuông ABCD theo hai cách khác nhau.
Video hướng dẫn giải
Trả lời câu hỏi Thực hành 4 trang 56 SGK Toán 9 Chân trời sáng tạo
Rút gọn các biểu thức sau:
a) \(\frac{2}{3}\sqrt {9{x^3}} + 4x\sqrt {\frac{x}{4}} - {x^2}\sqrt {\frac{1}{x}} \) với x > 0
b) \(\frac{{{a^2} - 5}}{{a + \sqrt {15} }}\) với a \( \ne - \sqrt 5 \)
Phương pháp giải:
Dựa vào VD6 trang 55 làm tương tự.
Lời giải chi tiết:
a) \(\frac{2}{3}\sqrt {9{x^3}} + 4x\sqrt {\frac{x}{4}} - {x^2}\sqrt {\frac{1}{x}} \)
\(\begin{array}{l} = \frac{2}{3}.3\sqrt {{x^2}.x} + 4x.\frac{1}{2}\sqrt x - \sqrt {{x^4}\frac{1}{x}} \\ = 2x\sqrt x + 2x\sqrt x - \sqrt {{x^3}} \\ = 4x\sqrt x - x\sqrt x \\ = 3x\sqrt x \end{array}\)
b) \(\frac{{{a^2} - 5}}{{a + \sqrt 5 }}\) với a \( \ne - \sqrt 5 \)
\(\frac{{{a^2} - 5}}{{a + \sqrt 5 }} = \frac{{\left( {a + \sqrt 5 } \right)\left( {a - \sqrt 5 } \right)}}{{a + \sqrt 5 }} = a - \sqrt 5 \)
Video hướng dẫn giải
Trả lời câu hỏi Thực hành 3 trang 55SGK Toán 9 Chân trời sáng tạo
Rút gọn các biểu thức sau:
a) \(\sqrt {20} - \sqrt 5 \)
b) \(\sqrt {32} - \sqrt {18} + \frac{4}{{\sqrt 2 }}\)
c) \(\left( {2 - \sqrt {10} } \right)\left( {\sqrt 2 - \sqrt 5 } \right)\)
Phương pháp giải:
Dựa vào VD5 trang 55 làm tương tự.
Lời giải chi tiết:
a) \(\sqrt {20} - \sqrt 5 = \sqrt {{2^2}.5} - \sqrt 5 = 2\sqrt 5 - \sqrt 5 = \sqrt 5 \)
b) \(\sqrt {32} - \sqrt {18} + \frac{4}{{\sqrt 2 }}\)\( = \sqrt {16.2} - \sqrt {9.2} + \frac{4\sqrt 2}{{2 }}\)\( = 4\sqrt 2 - 3\sqrt 2 + 2\sqrt 2\)\( = 3\sqrt 2\)
c) \(\left( {2 - \sqrt {10} } \right)\left( {\sqrt 2 - \sqrt 5 } \right)\)\( = 2\sqrt 2 - 2\sqrt 5 - \sqrt {10}.\sqrt 2 + \sqrt {10} .\sqrt 5 \)\( = 2\sqrt 2 - 2\sqrt 5 - \sqrt {20} + \sqrt {50}\)\( = 2\sqrt 2 - 2\sqrt 5 - 2\sqrt 5 + 5\sqrt 2\)\( = \left(2\sqrt 2 + 5\sqrt 2 \right) - \left(2\sqrt 5 + 2\sqrt 5\right)\)\( = 7\sqrt 2 - 4\sqrt 5\)
Video hướng dẫn giải
Trả lời câu hỏi Hoạt động 2 trang 54 SGK Toán 9 Chân trời sáng tạo
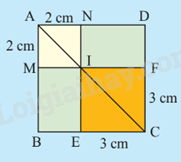
Hình vuông ABCD được chia thành hai hình vuông và hai hình chữ nhật như Hình 3.
a) Tính độ dài đường chéo của hai hình vuông AMIN và CEIF.
b) Tính độ dài đường chéo của hai hình vuông ABCD theo hai cách khác nhau.
Phương pháp giải:
- Tính độ dài đường chéo AMIN bằng cách dựa vào định lý Pythagore vào tam giác vuông AMI và tính độ dài đường chéo EIFC bằng cách dựa vào định lý Pythagore vào tam giác vuông IFC.- C1: Từ phần a suy ra độ dài đường chéo ABCD = độ dài đường chéo AMNI + độ dài đường chéo IFCE.- C2: Tính độ dài cạnh AB và BC suy ra đường chéo hình vuông ABCD bằng cách áp dụng định lý Pythagore vào tam giác vuông ABC.
Lời giải chi tiết:
a)Xét tam giác vuông AMI có AI = \(\sqrt {{2^2} + {2^2}} = 2\sqrt 2 \)cm
Vậy độ dài đường chéo AMIN bằng \(2\sqrt 2 \) cm
Xét tam giác vuông IFC có IC = \(\sqrt {{3^2} + {3^2}} = 3\sqrt 2 \)cm
Vậy độ dài đường chéo AMIN bằng \(3\sqrt 2 \) cm.
b) Cách 1:
Ta có: độ dài đường chéo ABCD = độ dài đường chéo AMNI + độ dài đường chéo IFCE = \(2\sqrt 2 \) + \(3\sqrt 2 \) = \(5\sqrt 2 \) cm.
Cách 2:
Độ dài cạnh AB là : 2 + 3 = 5 cm
Độ dài cạnh BC là : 2 + 3 = 5 cm
Xét tam giác vuông ABC có: AC = \(\sqrt {A{B^2} + B{C^2}} = \sqrt {{5^2} + {5^2}} = 5\sqrt 2 \) cm.
Vậy độ dài đường chéo của hình vuông ABCD là \(5\sqrt 2 \) cm.
Video hướng dẫn giải
Trả lời câu hỏi Vận dụng 2 trang 56 SGK Toán 9 Chân trời sáng tạo
Trả lời câu hỏi trong hoạt động khởi động trang 52.
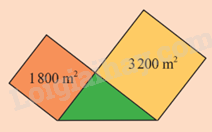
Một khu đất hình tam giác vuông tiếp giáp với hai thửa ruộng hình vuông có diện tích như hình bên. Khu đất hình tam giác vuông có chu vi bằng chu vi thửa ruộng bé không? Kiểm tra bằng cách nào?
Phương pháp giải:
- Tính cạnh thửa ruộng bé hình vuông và cạnh thửa ruộng lớn hình vuông.
- Tính cạnh còn lại của tam giác vuông bằng cách áp dụng định lý pythagore khi biết 2 cạnh của 2 hình vuông.
- Tính chu vi hình vuông bé và chu vi tam giác vuông và so sánh.
Lời giải chi tiết:
Cạnh thửa ruộng bé hình vuông là: \(\sqrt {1800} = 30\sqrt 2 \)m.
Chu vi thửa ruộng bé là: \(30\sqrt 2 .4 = 120\sqrt 2 \)m
Cạnh thửa ruộng lớn hình vuông là: \(\sqrt {3200} = 40\sqrt 2 \) m
Cạnh huyền của tam giác vuông là: \(\sqrt {{{(30\sqrt 2 )}^2} + {{(40\sqrt 2 )}^2}} = 50\sqrt 2 \) m
Chu vi tam giác vuông là: \(30\sqrt 2 + 40\sqrt 2 + 50\sqrt 2 = 120\sqrt 2 \) m.
Vậy khu đất hình tam giác vuông có chu vi bằng chu vi thửa ruộng bé.
Video hướng dẫn giải
Trả lời câu hỏi Hoạt động 2 trang 54 SGK Toán 9 Chân trời sáng tạo
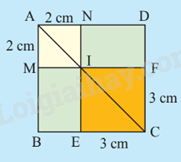
Hình vuông ABCD được chia thành hai hình vuông và hai hình chữ nhật như Hình 3.
a) Tính độ dài đường chéo của hai hình vuông AMIN và CEIF.
b) Tính độ dài đường chéo của hai hình vuông ABCD theo hai cách khác nhau.
Phương pháp giải:
- Tính độ dài đường chéo AMIN bằng cách dựa vào định lý Pythagore vào tam giác vuông AMI và tính độ dài đường chéo EIFC bằng cách dựa vào định lý Pythagore vào tam giác vuông IFC.- C1: Từ phần a suy ra độ dài đường chéo ABCD = độ dài đường chéo AMNI + độ dài đường chéo IFCE.- C2: Tính độ dài cạnh AB và BC suy ra đường chéo hình vuông ABCD bằng cách áp dụng định lý Pythagore vào tam giác vuông ABC.
Lời giải chi tiết:
a)Xét tam giác vuông AMI có AI = \(\sqrt {{2^2} + {2^2}} = 2\sqrt 2 \)cm
Vậy độ dài đường chéo AMIN bằng \(2\sqrt 2 \) cm
Xét tam giác vuông IFC có IC = \(\sqrt {{3^2} + {3^2}} = 3\sqrt 2 \)cm
Vậy độ dài đường chéo AMIN bằng \(3\sqrt 2 \) cm.
b) Cách 1:
Ta có: độ dài đường chéo ABCD = độ dài đường chéo AMNI + độ dài đường chéo IFCE = \(2\sqrt 2 \) + \(3\sqrt 2 \) = \(5\sqrt 2 \) cm.
Cách 2:
Độ dài cạnh AB là : 2 + 3 = 5 cm
Độ dài cạnh BC là : 2 + 3 = 5 cm
Xét tam giác vuông ABC có: AC = \(\sqrt {A{B^2} + B{C^2}} = \sqrt {{5^2} + {5^2}} = 5\sqrt 2 \) cm.
Vậy độ dài đường chéo của hình vuông ABCD là \(5\sqrt 2 \) cm.
Video hướng dẫn giải
Trả lời câu hỏi Thực hành 3 trang 55SGK Toán 9 Chân trời sáng tạo
Rút gọn các biểu thức sau:
a) \(\sqrt {20} - \sqrt 5 \)
b) \(\sqrt {32} - \sqrt {18} + \frac{4}{{\sqrt 2 }}\)
c) \(\left( {2 - \sqrt {10} } \right)\left( {\sqrt 2 - \sqrt 5 } \right)\)
Phương pháp giải:
Dựa vào VD5 trang 55 làm tương tự.
Lời giải chi tiết:
a) \(\sqrt {20} - \sqrt 5 = \sqrt {{2^2}.5} - \sqrt 5 = 2\sqrt 5 - \sqrt 5 = \sqrt 5 \)
b) \(\sqrt {32} - \sqrt {18} + \frac{4}{{\sqrt 2 }}\)\( = \sqrt {16.2} - \sqrt {9.2} + \frac{4\sqrt 2}{{2 }}\)\( = 4\sqrt 2 - 3\sqrt 2 + 2\sqrt 2\)\( = 3\sqrt 2\)
c) \(\left( {2 - \sqrt {10} } \right)\left( {\sqrt 2 - \sqrt 5 } \right)\)\( = 2\sqrt 2 - 2\sqrt 5 - \sqrt {10}.\sqrt 2 + \sqrt {10} .\sqrt 5 \)\( = 2\sqrt 2 - 2\sqrt 5 - \sqrt {20} + \sqrt {50}\)\( = 2\sqrt 2 - 2\sqrt 5 - 2\sqrt 5 + 5\sqrt 2\)\( = \left(2\sqrt 2 + 5\sqrt 2 \right) - \left(2\sqrt 5 + 2\sqrt 5\right)\)\( = 7\sqrt 2 - 4\sqrt 5\)
Video hướng dẫn giải
Trả lời câu hỏi Thực hành 4 trang 56 SGK Toán 9 Chân trời sáng tạo
Rút gọn các biểu thức sau:
a) \(\frac{2}{3}\sqrt {9{x^3}} + 4x\sqrt {\frac{x}{4}} - {x^2}\sqrt {\frac{1}{x}} \) với x > 0
b) \(\frac{{{a^2} - 5}}{{a + \sqrt {15} }}\) với a \( \ne - \sqrt 5 \)
Phương pháp giải:
Dựa vào VD6 trang 55 làm tương tự.
Lời giải chi tiết:
a) \(\frac{2}{3}\sqrt {9{x^3}} + 4x\sqrt {\frac{x}{4}} - {x^2}\sqrt {\frac{1}{x}} \)
\(\begin{array}{l} = \frac{2}{3}.3\sqrt {{x^2}.x} + 4x.\frac{1}{2}\sqrt x - \sqrt {{x^4}\frac{1}{x}} \\ = 2x\sqrt x + 2x\sqrt x - \sqrt {{x^3}} \\ = 4x\sqrt x - x\sqrt x \\ = 3x\sqrt x \end{array}\)
b) \(\frac{{{a^2} - 5}}{{a + \sqrt 5 }}\) với a \( \ne - \sqrt 5 \)
\(\frac{{{a^2} - 5}}{{a + \sqrt 5 }} = \frac{{\left( {a + \sqrt 5 } \right)\left( {a - \sqrt 5 } \right)}}{{a + \sqrt 5 }} = a - \sqrt 5 \)
Video hướng dẫn giải
Trả lời câu hỏi Vận dụng 2 trang 56 SGK Toán 9 Chân trời sáng tạo
Trả lời câu hỏi trong hoạt động khởi động trang 52.
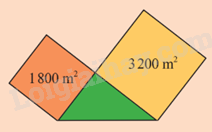
Một khu đất hình tam giác vuông tiếp giáp với hai thửa ruộng hình vuông có diện tích như hình bên. Khu đất hình tam giác vuông có chu vi bằng chu vi thửa ruộng bé không? Kiểm tra bằng cách nào?
Phương pháp giải:
- Tính cạnh thửa ruộng bé hình vuông và cạnh thửa ruộng lớn hình vuông.
- Tính cạnh còn lại của tam giác vuông bằng cách áp dụng định lý pythagore khi biết 2 cạnh của 2 hình vuông.
- Tính chu vi hình vuông bé và chu vi tam giác vuông và so sánh.
Lời giải chi tiết:
Cạnh thửa ruộng bé hình vuông là: \(\sqrt {1800} = 30\sqrt 2 \)m.
Chu vi thửa ruộng bé là: \(30\sqrt 2 .4 = 120\sqrt 2 \)m
Cạnh thửa ruộng lớn hình vuông là: \(\sqrt {3200} = 40\sqrt 2 \) m
Cạnh huyền của tam giác vuông là: \(\sqrt {{{(30\sqrt 2 )}^2} + {{(40\sqrt 2 )}^2}} = 50\sqrt 2 \) m
Chu vi tam giác vuông là: \(30\sqrt 2 + 40\sqrt 2 + 50\sqrt 2 = 120\sqrt 2 \) m.
Vậy khu đất hình tam giác vuông có chu vi bằng chu vi thửa ruộng bé.
Mục 2 của chương trình Toán 9 tập 1 - Chân trời sáng tạo tập trung vào việc ôn tập và hệ thống hóa kiến thức về hàm số bậc nhất. Các bài tập trong mục này yêu cầu học sinh vận dụng các kiến thức đã học để giải quyết các bài toán thực tế, đồng thời rèn luyện kỹ năng tư duy logic và khả năng giải quyết vấn đề.
Bài tập này yêu cầu học sinh xác định các yếu tố của hàm số bậc nhất (hệ số a, b), vẽ đồ thị hàm số, và tìm các điểm thuộc đồ thị. Để giải bài tập này, học sinh cần nắm vững định nghĩa hàm số bậc nhất, các tính chất của đồ thị hàm số, và các phương pháp vẽ đồ thị.
Bài tập này đưa ra các bài toán thực tế liên quan đến hàm số bậc nhất, yêu cầu học sinh xây dựng mô hình toán học và giải quyết bài toán. Ví dụ, bài toán về việc tính tiền điện, tiền nước, hoặc tính quãng đường đi được trong một khoảng thời gian nhất định. Để giải bài tập này, học sinh cần biết cách chuyển đổi các thông tin thực tế thành các biểu thức toán học, và sử dụng các kiến thức về hàm số bậc nhất để giải quyết bài toán.
Bài tập này cung cấp một loạt các câu hỏi trắc nghiệm về hàm số bậc nhất, giúp học sinh kiểm tra lại kiến thức đã học và rèn luyện kỹ năng làm bài trắc nghiệm. Các câu hỏi trắc nghiệm thường tập trung vào các khái niệm cơ bản, các tính chất của đồ thị hàm số, và các ứng dụng của hàm số bậc nhất.
Dưới đây là hướng dẫn giải chi tiết cho từng bài tập trong mục 2 trang 54, 55, 56 SGK Toán 9 tập 1 - Chân trời sáng tạo:
Ngoài sách giáo khoa, học sinh có thể tham khảo thêm các tài liệu sau để học tốt môn Toán 9:
Hy vọng rằng với hướng dẫn chi tiết này, các em học sinh sẽ giải quyết thành công các bài tập trong mục 2 trang 54, 55, 56 SGK Toán 9 tập 1 - Chân trời sáng tạo. Chúc các em học tập tốt!