Giaitoan.edu.vn xin giới thiệu lời giải chi tiết mục 1 trang 90, 91 SGK Toán 9 tập 1 - Chân trời sáng tạo. Bài viết này cung cấp đáp án đầy đủ, dễ hiểu, cùng với phương pháp giải bài tập hiệu quả, giúp học sinh nắm vững kiến thức và tự tin làm bài tập.
Chúng tôi luôn cập nhật nhanh chóng và chính xác các lời giải bài tập Toán 9, đáp ứng nhu cầu học tập của học sinh trên toàn quốc.
Cho hai điểm A, B trên đường tròn (O; R). Nêu nhận xét về đỉnh và cạnh của (widehat {AOB})
Video hướng dẫn giải
Trả lời câu hỏi Vận dụng 1 trang 91 SGK Toán 9 Chân trời sáng tạo
Tính số đo góc ở tâm được tạo thành khi kim giờ quay:
a) Từ 7 giờ đến 9 giờ
b) Từ 9 giờ đến 12 giờ
Phương pháp giải:
Dựa vào đồng hồ như 1 đường tròn có 12 phần, tổng góc của đường tròn bằng 360o .
Ta tính 1 giờ quay được bao nhiêu độ rồi tính 7 giờ đến 9 giờ và 9 giờ đến 12 giờ.
Lời giải chi tiết:
Ta có mỗi giờ thì kim giờ quay được \(\frac{{{{360}^0}}}{{12}} = {30^o}\)
a) Vậy từ 7 giờ đến 9 giờ, kim giờ quay được \({30^o}(9 - 7) = {60^o}\)
b) Vậy từ 9 giờ đến 12 giờ, kim giờ quay được \({30^o}(12 - 9) = {90^o}\)
Video hướng dẫn giải
Trả lời câu hỏi Hoạt động 1 trang 90SGK Toán 9 Chân trời sáng tạo
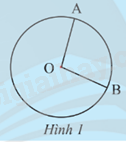
Cho hai điểm A, B trên đường tròn (O; R). Nêu nhận xét về đỉnh và cạnh của \(\widehat {AOB}\)
Phương pháp giải:
Nhìn hình và nhận xét.
Lời giải chi tiết:
Đỉnh của \(\widehat {AOB}\) trùng với tâm O của đường tròn (O; R)
Cạnh của \(\widehat {AOB}\) là OA và OB đều bằng bán kính R.
Video hướng dẫn giải
Trả lời câu hỏi Thực hành 1 trang 90 SGK Toán 9 Chân trời sáng tạo
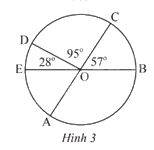
Tính số đo góc ở tâm \(\widehat {EOA}\) và \(\widehat {AOB}\) trong Hình 3. Biết AC và BE là hai đường kính của đường tròn (O).
Phương pháp giải:
Dựa vào tổng góc của đường tròn bằng 360o.
Lời giải chi tiết:
Ta có AC là đường kính chia đường tròn tâm (O) thành hai phần bằng nhau, mỗi góc là 180o.
Suy ra ta có \(\widehat {EOA} = {180^o} - \widehat {COD} - \widehat {DOE} = {180^o} - {95^o} - {28^o} = {57^o}\)
Tương tự , ta có: \(\widehat {AOB} = {180^o} - \widehat {COB} = {180^o} - {57^o} = {123^o}\)
Video hướng dẫn giải
Trả lời câu hỏi Hoạt động 1 trang 90SGK Toán 9 Chân trời sáng tạo
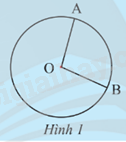
Cho hai điểm A, B trên đường tròn (O; R). Nêu nhận xét về đỉnh và cạnh của \(\widehat {AOB}\)
Phương pháp giải:
Nhìn hình và nhận xét.
Lời giải chi tiết:
Đỉnh của \(\widehat {AOB}\) trùng với tâm O của đường tròn (O; R)
Cạnh của \(\widehat {AOB}\) là OA và OB đều bằng bán kính R.
Video hướng dẫn giải
Trả lời câu hỏi Thực hành 1 trang 90 SGK Toán 9 Chân trời sáng tạo
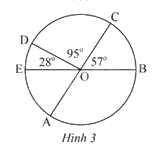
Tính số đo góc ở tâm \(\widehat {EOA}\) và \(\widehat {AOB}\) trong Hình 3. Biết AC và BE là hai đường kính của đường tròn (O).
Phương pháp giải:
Dựa vào tổng góc của đường tròn bằng 360o.
Lời giải chi tiết:
Ta có AC là đường kính chia đường tròn tâm (O) thành hai phần bằng nhau, mỗi góc là 180o.
Suy ra ta có \(\widehat {EOA} = {180^o} - \widehat {COD} - \widehat {DOE} = {180^o} - {95^o} - {28^o} = {57^o}\)
Tương tự , ta có: \(\widehat {AOB} = {180^o} - \widehat {COB} = {180^o} - {57^o} = {123^o}\)
Video hướng dẫn giải
Trả lời câu hỏi Vận dụng 1 trang 91 SGK Toán 9 Chân trời sáng tạo
Tính số đo góc ở tâm được tạo thành khi kim giờ quay:
a) Từ 7 giờ đến 9 giờ
b) Từ 9 giờ đến 12 giờ
Phương pháp giải:
Dựa vào đồng hồ như 1 đường tròn có 12 phần, tổng góc của đường tròn bằng 360o .
Ta tính 1 giờ quay được bao nhiêu độ rồi tính 7 giờ đến 9 giờ và 9 giờ đến 12 giờ.
Lời giải chi tiết:
Ta có mỗi giờ thì kim giờ quay được \(\frac{{{{360}^0}}}{{12}} = {30^o}\)
a) Vậy từ 7 giờ đến 9 giờ, kim giờ quay được \({30^o}(9 - 7) = {60^o}\)
b) Vậy từ 9 giờ đến 12 giờ, kim giờ quay được \({30^o}(12 - 9) = {90^o}\)
Mục 1 trang 90, 91 SGK Toán 9 tập 1 - Chân trời sáng tạo thuộc chương trình học về hàm số bậc nhất. Đây là một phần quan trọng trong chương trình Toán 9, giúp học sinh hiểu rõ hơn về khái niệm hàm số, cách xác định hàm số và ứng dụng của hàm số trong giải quyết các bài toán thực tế.
Mục 1 tập trung vào việc ôn tập và mở rộng kiến thức về hàm số bậc nhất. Cụ thể, học sinh sẽ được làm quen với các nội dung sau:
Bài 1 yêu cầu học sinh xác định các hệ số a, b của hàm số bậc nhất y = ax + b dựa vào đồ thị hàm số. Để giải bài này, học sinh cần nắm vững cách đọc tọa độ điểm trên đồ thị và áp dụng công thức tính hệ số.
Ví dụ: Nếu đồ thị hàm số đi qua hai điểm A(x1, y1) và B(x2, y2) thì ta có hệ phương trình:
Giải hệ phương trình này, ta sẽ tìm được giá trị của a và b.
Bài 2 yêu cầu học sinh vẽ đồ thị hàm số bậc nhất y = ax + b. Để vẽ đồ thị, học sinh cần xác định ít nhất hai điểm thuộc đồ thị hàm số. Sau đó, nối hai điểm này lại với nhau để được đồ thị hàm số.
Lưu ý: Nếu a > 0 thì đồ thị hàm số là đường thẳng đi lên. Nếu a < 0 thì đồ thị hàm số là đường thẳng đi xuống.
Bài 3 yêu cầu học sinh giải các bài toán ứng dụng liên quan đến hàm số bậc nhất. Để giải bài này, học sinh cần đọc kỹ đề bài, xác định các yếu tố liên quan đến hàm số và xây dựng phương trình hàm số phù hợp.
Ví dụ: Một người đi xe đạp với vận tốc 15 km/h. Quãng đường đi được sau t giờ là hàm số của thời gian t. Hãy viết hàm số biểu thị quãng đường đi được theo thời gian t.
Giải: Hàm số biểu thị quãng đường đi được theo thời gian t là s = 15t (km).
Hy vọng bài giải chi tiết mục 1 trang 90, 91 SGK Toán 9 tập 1 - Chân trời sáng tạo này sẽ giúp các em học sinh hiểu rõ hơn về kiến thức và kỹ năng giải bài tập về hàm số bậc nhất. Chúc các em học tập tốt!