Chào mừng bạn đến với bài học về lý thuyết Hình cầu trong chương trình Toán 9 Chân trời sáng tạo. Bài học này sẽ cung cấp cho bạn những kiến thức cơ bản và quan trọng nhất về hình cầu, bao gồm định nghĩa, các yếu tố của hình cầu, công thức tính diện tích bề mặt và thể tích.
Chúng tôi tại giaitoan.edu.vn cam kết mang đến cho bạn trải nghiệm học toán online hiệu quả và thú vị nhất.
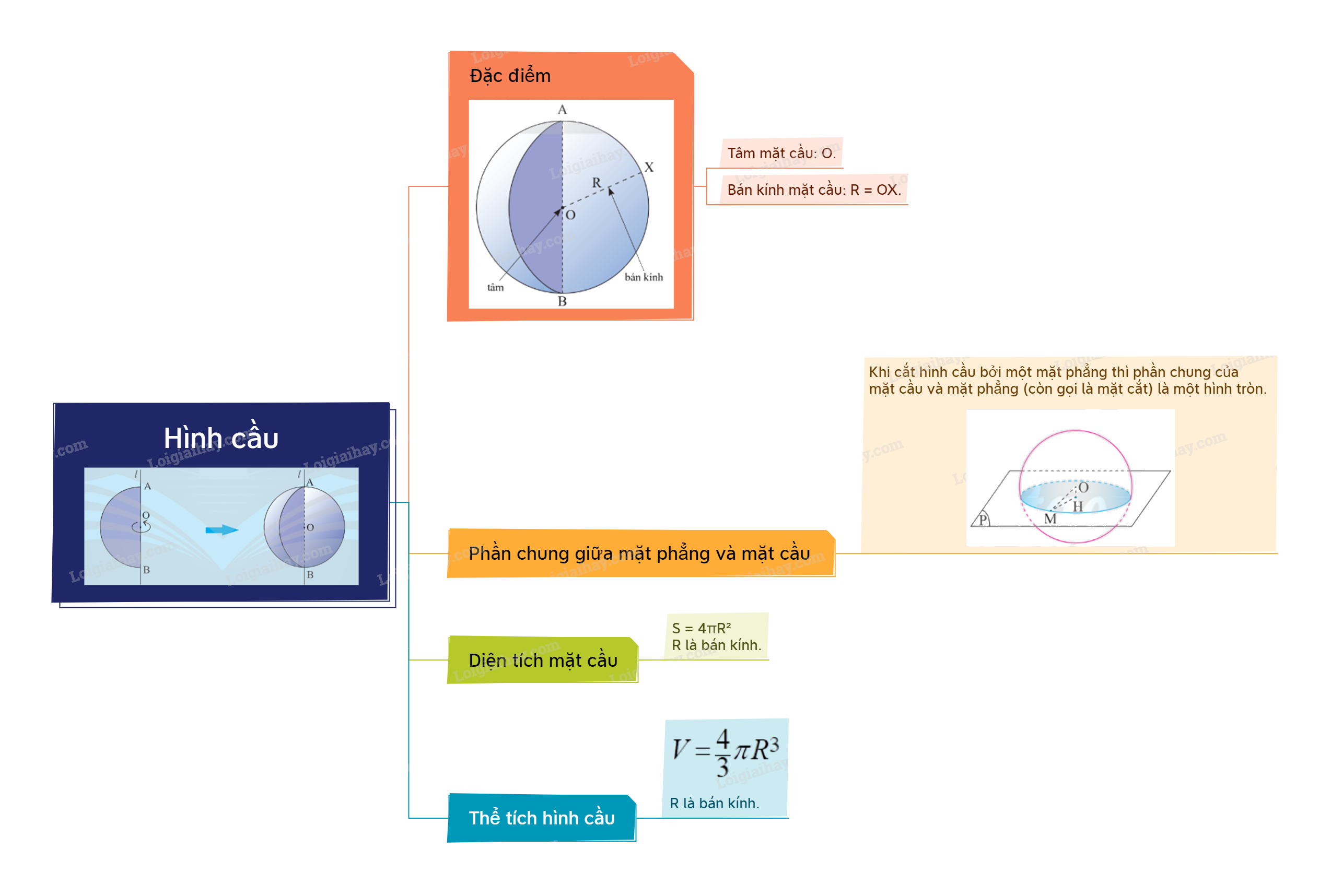
1. Hình cầu Định nghĩa Khi quay nửa hình tròn tâm O, bán kính R một vòng quanh đường kính AB cố định ta được một hình cầu tâm O, bán kính R. Khi đó, nửa đường tròn quét thành một mặt cầu. Ta cũng gọi O và R lần lượt là tâm và bán kính của mặt cầu đó. Đoạn thẳng đi qua tâm của hình cầu với hai đầu mút nằm trên mặt cầu gọi là đường kính của hình cầu (hay mặt cầu).
1. Hình cầu

Định nghĩa
Khi quay nửa hình tròn tâm O, bán kính R một vòng quanh đường kính AB cố định ta được một hình cầu tâm O, bán kính R.
Khi đó, nửa đường tròn quét thành một mặt cầu. Ta cũng gọi O và R lần lượt là tâm và bán kính của mặt cầu đó. Đoạn thẳng đi qua tâm của hình cầu với hai đầu mút nằm trên mặt cầu gọi là đường kính của hình cầu (hay mặt cầu). |
Phần chung của mặt phẳng và mặt cầu
Khi cắt hình cầu bởi một mặt phẳng thì phần chung của mặt cầu và mặt phẳng (còn gọi là mặt cắt) là một hình tròn.
|
2. Diện tích của mặt cầu
Diện tích S của mặt cầu có bán kính R là: \(S = 4\pi {R^2}\). |
Ví dụ:
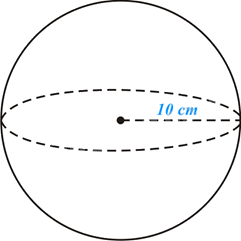
Diện tích mặt cầu là:
\(S = 4\pi {R^2} = 4\pi {.10^2} = 400\pi \left( {c{m^2}} \right)\),
3. Thể tích hình cầu
Thể tích của hình cầu có bán kính R là \(V = \frac{4}{3}\pi {R^3}\). |
Ví dụ:
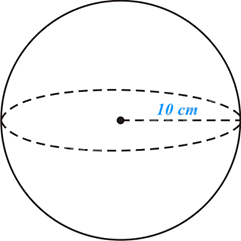
Thể tích hình cầu là:
\(V = \frac{4}{3}\pi {R^3} = \frac{4}{3}\pi {.10^3} = \frac{{4000\pi }}{3}\left( {c{m^3}} \right)\).
Hình cầu là một trong những hình khối quan trọng trong chương trình Hình học không gian lớp 9. Việc nắm vững lý thuyết và các công thức liên quan đến hình cầu là nền tảng để giải quyết các bài toán thực tế và chuẩn bị cho các kỳ thi quan trọng.
Hình cầu là tập hợp tất cả các điểm trong không gian cách một điểm cố định (gọi là tâm) một khoảng không đổi (gọi là bán kính).
Diện tích bề mặt của hình cầu được tính theo công thức:
S = 4πR2
Trong đó:
Thể tích của hình cầu được tính theo công thức:
V = (4/3)πR3
Trong đó:
Trong chương trình Toán 9, các bài toán liên quan đến hình cầu thường tập trung vào việc tính diện tích bề mặt và thể tích của hình cầu khi biết bán kính hoặc đường kính. Ngoài ra, còn có các bài toán liên quan đến việc tìm bán kính hoặc đường kính khi biết diện tích bề mặt hoặc thể tích.
Ví dụ 1: Tính diện tích bề mặt của hình cầu có bán kính R = 5cm.
Giải:
S = 4πR2 = 4 * 3.14159 * 52 = 314.159 cm2
Ví dụ 2: Tính thể tích của hình cầu có đường kính D = 10cm.
Giải:
R = D/2 = 10/2 = 5cm
V = (4/3)πR3 = (4/3) * 3.14159 * 53 = 523.598 cm3
Ngoài các công thức cơ bản, bạn có thể tìm hiểu thêm về các khái niệm liên quan đến hình cầu như:
Để nắm vững lý thuyết và các công thức về hình cầu, bạn nên luyện tập giải nhiều bài tập khác nhau. Bạn có thể tìm thấy các bài tập trong sách giáo khoa, sách bài tập, hoặc trên các trang web học toán online như giaitoan.edu.vn.
Hy vọng bài học này đã cung cấp cho bạn những kiến thức hữu ích về lý thuyết Hình cầu Toán 9 Chân trời sáng tạo. Chúc bạn học tập tốt!