Giaitoan.edu.vn xin giới thiệu lời giải chi tiết mục 3 trang 91 SGK Toán 9 tập 2 - Chân trời sáng tạo. Bài viết này cung cấp đáp án đầy đủ, phương pháp giải rõ ràng, giúp học sinh nắm vững kiến thức và tự tin làm bài tập.
Chúng tôi luôn cập nhật nhanh chóng và chính xác các lời giải bài tập Toán 9, đáp ứng nhu cầu học tập của học sinh trên toàn quốc. Hãy cùng giaitoan.edu.vn khám phá lời giải chi tiết ngay sau đây!
Lấy một cái gàu hình nón và một cái bình hình trụ (Hình 8a) có cùng bán kính đáy r và chiều cao h. Múc đầy nước vào gàu rồi đổ qua cái bình. Sau ba lần đổ nước như thế thì cái bình vừa đầy nước (Hình 8b). Tính theo r và h: a) Thể tích của bình hình trụ; b) Thể tích của gàu hình nón.
Video hướng dẫn giải
Trả lời câu hỏi Thực hành 4 trang 91 SGK Toán 9 Chân trời sáng tạo
Tính thể tích của hình nón có bán kính đáy 6 cm, chiều cao 4 cm.
Phương pháp giải:
Dựa vào: Thể tích V của hình nón có bán kính đáy r và chiều cao h là:
\(V = \frac{1}{3}Sh = \frac{1}{3}\pi {r^2}h\) (S là diện tích đáy của hình nón).
Lời giải chi tiết:
Thể tích của hình nón là: \(V = \frac{1}{3}\pi {r^2}h = \frac{1}{3}\pi {.6^2}.4 = 48\pi \) (cm3).
Video hướng dẫn giải
Trả lời câu hỏi Vận dụng trang 91 SGK Toán 9 Chân trời sáng tạo
Từ một khối gỗ có dạng hình lập phương cạnh 6 cm, người ta khoét một hình nón có đường kính mặt đáy là 4 cm và đỉnh của hình nón chạm vào mặt đáy của khối gỗ (Hình 10). Hãy tính thể tích của phần khối gỗ còn lại (kết quả làm tròn đến hàng đơn vị).
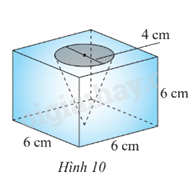
Phương pháp giải:
Dựa vào: Thể tích V của hình nón có bán kính đáy r và chiều cao h là:
\(V = \frac{1}{3}Sh = \frac{1}{3}\pi {r^2}h\) (S là diện tích đáy của hình nón).
Lời giải chi tiết:
Thể tích khối lập phương là: V = 63 = 216 (cm3).
Thể tích hình nón là: \(V' = \frac{1}{3}.\pi {r^2}h = \frac{1}{3}.\pi {\left( {\frac{4}{2}} \right)^2}.6 = 8\pi \) (cm3).
Thể tích khối gỗ còn lại là: V – V’ = 216 – 8\(\pi \) = 191 (cm3).
Video hướng dẫn giải
Trả lời câu hỏi Hoạt động 3 trang 91 SGK Toán 9 Chân trời sáng tạo
Lấy một cái gàu hình nón và một cái bình hình trụ (Hình 8a) có cùng bán kính đáy r và chiều cao h. Múc đầy nước vào gàu rồi đổ qua cái bình. Sau ba lần đổ nước như thế thì cái bình vừa đầy nước (Hình 8b). Tính theo r và h:
a) Thể tích của bình hình trụ;
b) Thể tích của gàu hình nón.
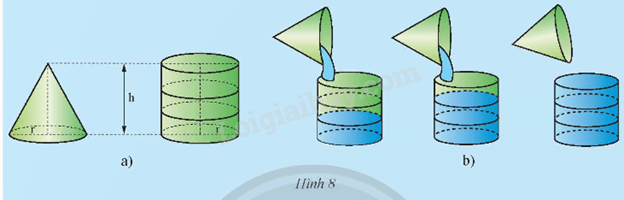
Phương pháp giải:
- Thể tích của hình trụ là: \(V = \pi {r^2}h\)
- Dựa vào: Thể tích V của hình nón có bán kính đáy r và chiều cao h là:
\(V = \frac{1}{3}Sh = \frac{1}{3}\pi {r^2}h\) (S là diện tích đáy của hình nón).
Lời giải chi tiết:
a) Thể tích của bình hình trụ là: \(V = \pi {r^2}h\)
b) Thể tích của gàu hình nón là: \(V' = \frac{V}{3} = \frac{{\pi {r^2}h}}{3}\).
Video hướng dẫn giải
Trả lời câu hỏi Hoạt động 3 trang 91 SGK Toán 9 Chân trời sáng tạo
Lấy một cái gàu hình nón và một cái bình hình trụ (Hình 8a) có cùng bán kính đáy r và chiều cao h. Múc đầy nước vào gàu rồi đổ qua cái bình. Sau ba lần đổ nước như thế thì cái bình vừa đầy nước (Hình 8b). Tính theo r và h:
a) Thể tích của bình hình trụ;
b) Thể tích của gàu hình nón.
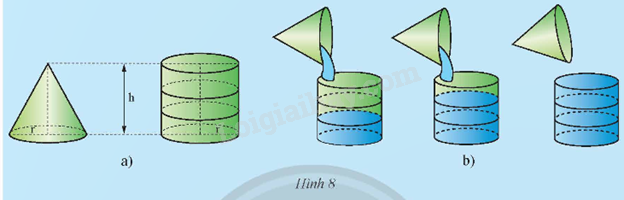
Phương pháp giải:
- Thể tích của hình trụ là: \(V = \pi {r^2}h\)
- Dựa vào: Thể tích V của hình nón có bán kính đáy r và chiều cao h là:
\(V = \frac{1}{3}Sh = \frac{1}{3}\pi {r^2}h\) (S là diện tích đáy của hình nón).
Lời giải chi tiết:
a) Thể tích của bình hình trụ là: \(V = \pi {r^2}h\)
b) Thể tích của gàu hình nón là: \(V' = \frac{V}{3} = \frac{{\pi {r^2}h}}{3}\).
Video hướng dẫn giải
Trả lời câu hỏi Thực hành 4 trang 91 SGK Toán 9 Chân trời sáng tạo
Tính thể tích của hình nón có bán kính đáy 6 cm, chiều cao 4 cm.
Phương pháp giải:
Dựa vào: Thể tích V của hình nón có bán kính đáy r và chiều cao h là:
\(V = \frac{1}{3}Sh = \frac{1}{3}\pi {r^2}h\) (S là diện tích đáy của hình nón).
Lời giải chi tiết:
Thể tích của hình nón là: \(V = \frac{1}{3}\pi {r^2}h = \frac{1}{3}\pi {.6^2}.4 = 48\pi \) (cm3).
Video hướng dẫn giải
Trả lời câu hỏi Vận dụng trang 91 SGK Toán 9 Chân trời sáng tạo
Từ một khối gỗ có dạng hình lập phương cạnh 6 cm, người ta khoét một hình nón có đường kính mặt đáy là 4 cm và đỉnh của hình nón chạm vào mặt đáy của khối gỗ (Hình 10). Hãy tính thể tích của phần khối gỗ còn lại (kết quả làm tròn đến hàng đơn vị).
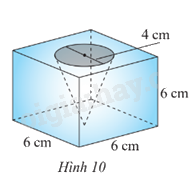
Phương pháp giải:
Dựa vào: Thể tích V của hình nón có bán kính đáy r và chiều cao h là:
\(V = \frac{1}{3}Sh = \frac{1}{3}\pi {r^2}h\) (S là diện tích đáy của hình nón).
Lời giải chi tiết:
Thể tích khối lập phương là: V = 63 = 216 (cm3).
Thể tích hình nón là: \(V' = \frac{1}{3}.\pi {r^2}h = \frac{1}{3}.\pi {\left( {\frac{4}{2}} \right)^2}.6 = 8\pi \) (cm3).
Thể tích khối gỗ còn lại là: V – V’ = 216 – 8\(\pi \) = 191 (cm3).
Mục 3 trang 91 SGK Toán 9 tập 2 - Chân trời sáng tạo thường xoay quanh các bài toán liên quan đến hàm số bậc hai, bao gồm việc xác định hệ số, tìm đỉnh parabol, vẽ đồ thị và ứng dụng vào giải quyết các bài toán thực tế. Việc nắm vững kiến thức về hàm số bậc hai là nền tảng quan trọng cho các chương trình học tiếp theo.
Bài tập trong mục 3 thường yêu cầu học sinh:
Để giúp học sinh hiểu rõ hơn, chúng ta sẽ đi vào giải chi tiết từng bài tập trong mục 3 trang 91:
Ví dụ: Cho hàm số y = 2x2 - 5x + 3. Xác định hệ số a, b, c.
Lời giải: a = 2, b = -5, c = 3.
Ví dụ: Cho hàm số y = x2 - 4x + 1. Tính tọa độ đỉnh của parabol.
Lời giải:
Ví dụ: Vẽ đồ thị hàm số y = x2 - 2x - 1.
Lời giải:
Để giải các bài toán về hàm số bậc hai một cách hiệu quả, học sinh cần:
Hàm số bậc hai có nhiều ứng dụng trong thực tế, ví dụ như:
Trong quá trình học tập, học sinh cần chú ý:
Hy vọng rằng với lời giải chi tiết và phương pháp giải rõ ràng, học sinh có thể tự tin giải các bài tập trong mục 3 trang 91 SGK Toán 9 tập 2 - Chân trời sáng tạo. Chúc các em học tập tốt!