Chào mừng bạn đến với giaitoan.edu.vn, nơi cung cấp lời giải chi tiết và dễ hiểu cho các bài tập Toán 9 tập 1. Bài viết này sẽ hướng dẫn bạn giải bài tập 4 trang 71 SGK Toán 9 tập 1 - Chân trời sáng tạo một cách nhanh chóng và hiệu quả.
Chúng tôi hiểu rằng việc giải toán đôi khi có thể gặp khó khăn. Vì vậy, chúng tôi đã biên soạn lời giải chi tiết, kèm theo các bước giải rõ ràng, giúp bạn nắm vững kiến thức và tự tin hơn trong quá trình học tập.
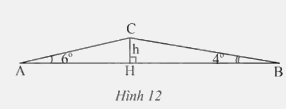
Lúc 6 giờ sáng, bạn An đi xe đạp từ nhà (điểm A) đến trường (điểm B). Khi đi từ A đến B, An phải đi đoạn lên dốc AC và đoạn xuống dốc CB (Hình 12). Biết AB = 762m, (widehat A = {6^o},widehat B = {4^o}). a) Tính chiều cao h của con dốc b) Hỏi bạn An đến trường lúc mấy giờ? Biết rằng tốc độ khi lên dốc là 4 km/h và tốc độ khi xuống dốc là 19 km/h.
Đề bài
Lúc 6 giờ sáng, bạn An đi xe đạp từ nhà (điểm A) đến trường (điểm B). Khi đi từ A đến B, An phải đi đoạn lên dốc AC và đoạn xuống dốc CB (Hình 12). Biết AB = 762m, \(\widehat A = {6^o},\widehat B = {4^o}\).
a) Tính chiều cao h của con dốc
b) Hỏi bạn An đến trường lúc mấy giờ? Biết rằng tốc độ khi lên dốc là 4 km/h và tốc độ khi xuống dốc là 19 km/h.
Video hướng dẫn giải
Phương pháp giải - Xem chi tiết
Đặt AH = x sau đó áp dụng hệ thức về cạnh và góc trong tam giác vuông để viết biểu thức chiều cao h theo x. Giải phương trình ta tìm được h.
Áp dụng công thức quãng đường = thời gian . vận tốc để rút ra tính thời gian.
Lời giải chi tiết
a) Đặt AH = x (m) (0 < x < 762)
Suy ra BH = 762 – x (m). Áp dụng hệ thức về cạnh và góc trong tam giác vuông, ta có:
h = x. tan \({6^o}\) và h = (762 – x). tan \({4^o}\)
Suy ra x. tan \({6^o}\)= (762 – x). tan \({4^o}\)
x.( tan \({6^o}\)+ tan \({4^o}\)) =762. tan \({4^o}\)
x = \(\frac{{762.\tan {4^o}}}{{\tan {6^o} + \tan {4^o}}}\)
Vậy h = \(\frac{{762.\tan {4^o}}}{{\tan {6^o} + \tan {4^o}}}\). tan \({6^o}\)\( \approx \) 32 m.
b) Xét tam giác AHC vuông tại H, \(\widehat A = {6^o}\), ta có:
\(AC = \frac{h}{{\sin A}} = \frac{{32}}{{\sin {6^o}}} \approx 306m\) = 0,306 km
Xét tam giác BHC vuông tại H, \(\widehat B = {4^o}\), ta có:
\(CB = \frac{h}{{\sin B}} = \frac{{32}}{{\sin {4^o}}} \approx 459m\) = 0,459 km
Thời gian An đi từ nhà tới trường là:
\(t = \frac{{AC}}{4} + \frac{{BC}}{{19}} = \frac{{0,306}}{4} + \frac{{0,459}}{{19}} \approx 0,1\) (h) = 6 phút.
Vậy An đến trường khoảng 6 giờ 6 phút.
Bài tập 4 trang 71 SGK Toán 9 tập 1 - Chân trời sáng tạo thuộc chương trình học về hàm số bậc nhất. Bài tập này yêu cầu học sinh vận dụng kiến thức về hàm số bậc nhất để giải quyết các bài toán thực tế. Dưới đây là hướng dẫn chi tiết cách giải bài tập này:
Trước khi đi vào giải bài tập, chúng ta cần ôn lại một số kiến thức cơ bản về hàm số bậc nhất:
Bài tập 4 trang 71 SGK Toán 9 tập 1 - Chân trời sáng tạo thường có dạng bài toán yêu cầu xác định hàm số bậc nhất khi biết các thông tin về đồ thị hoặc các điểm thuộc đồ thị. Để giải bài tập này, chúng ta cần:
Đề bài: (Giả sử đề bài cụ thể ở đây) Cho hai điểm A(1; 2) và B(-1; 0). Hãy tìm hàm số bậc nhất y = ax + b đi qua hai điểm A và B.
Giải:
Vì hàm số y = ax + b đi qua điểm A(1; 2) nên ta có phương trình: 2 = a(1) + b => a + b = 2 (1)
Vì hàm số y = ax + b đi qua điểm B(-1; 0) nên ta có phương trình: 0 = a(-1) + b => -a + b = 0 (2)
Từ (1) và (2) ta có hệ phương trình:
| a | b |
|---|---|
| 1 | 1 |
| -1 | 1 |
Giải hệ phương trình này, ta được a = 1 và b = 1.
Vậy hàm số bậc nhất cần tìm là y = x + 1.
Để nắm vững kiến thức về hàm số bậc nhất và rèn luyện kỹ năng giải bài tập, bạn có thể thực hiện các bài tập sau:
Ngoài việc giải bài tập, bạn có thể tìm hiểu thêm về các ứng dụng của hàm số bậc nhất trong thực tế, chẳng hạn như:
Hy vọng bài viết này đã giúp bạn hiểu rõ hơn về cách giải bài tập 4 trang 71 SGK Toán 9 tập 1 - Chân trời sáng tạo. Chúc bạn học tập tốt!