Chào mừng các em học sinh đến với chuyên mục giải bài tập Toán 9 tập 1 của giaitoan.edu.vn. Ở bài viết này, chúng tôi sẽ cung cấp lời giải chi tiết và dễ hiểu cho các bài tập trong mục 4, trang 78, 79 và 80 của sách giáo khoa Toán 9 tập 1 - Chân trời sáng tạo.
Mục tiêu của chúng tôi là giúp các em nắm vững kiến thức, rèn luyện kỹ năng giải toán và tự tin hơn trong học tập.
Tìm số điểm chung của hai đường tròn (O) và (O’) trong mỗi trường hợp sau:
Video hướng dẫn giải
Trả lời câu hỏi Thực hành 3 trang 80 SGK Toán 9 Chân trời sáng tạo
Xác định vị trí tương đối giữa hai đường tròn (I;R) và (J;R’) trong mỗi trường hợp sau:
a) IJ = 5; R = 3; R’ = 2
b) IJ = 4; R = 11; R’ = 7
c) IJ = 6; R = 9; R’ = 4
d) IJ = 10; R = 4; R’ = 1
Phương pháp giải:
Dựa vào VD5 trang 80 làm tương tự.
Lời giải chi tiết:
a) Ta có 5 = 3 + 2 nên IJ = R + R’, suy ra hai đường tròn (I;R) và (J;R’) tiếp xúc ngoài.
b) Ta có 4 = 11 – 7 nên IJ = R - R’, suy ra hai đường tròn (I;R) và (J;R’) tiếp xúc trong.
c) Ta có 9 – 4 < 6 < 9 + 4 nên R - R’ < IJ < R + R’, suy ra hai đường tròn (I;R) và (J;R’) cắt nhau.
d) Ta có 10 > 4 + 1 nên IJ > R - R’, suy ra hai đường tròn (I;R) và (J;R’) ở ngoài nhau.
Video hướng dẫn giải
Trả lời câu hỏi Hoạt động 4 trang 78 SGK Toán 9 Chân trời sáng tạo
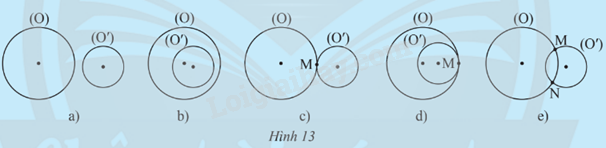
Tìm số điểm chung của hai đường tròn (O) và (O’) trong mỗi trường hợp sau:
Phương pháp giải:
Nhìn vào hình để xác định điểm chung của hai đường tròn.
Lời giải chi tiết:
a) Không có điểm chung
b) Không có điểm chung
c) Một điểm chung M
d) Một điểm chung M
e) Hai điểm chung M và N.
Video hướng dẫn giải
Trả lời câu hỏi Vận dụng 3 trang 81 SGK Toán 9 Chân trời sáng tạo
Mô tả vị trí tương đối giữa mỗi cặp đường tròn trong hình chụp bộ cồng chiêng Tây Nguyên trong Hình 18.

Phương pháp giải:
Dựa vào định nghĩa về vị trí tương đối của hai đường tròn để xác định.
Lời giải chi tiết:
a) Hai đường tròn không giao nhau
b) Hai đường tròn tiếp xúc nhau
c) Hai đường tròn cắt nhau.
Video hướng dẫn giải
Trả lời câu hỏi Hoạt động 5 trang 79SGK Toán 9 Chân trời sáng tạo
Cho hai đường tròn phân biệt (O;R) và (O’;R’) với R \( \ge \) R’.
Hãy so sánh OO’ với R + R’ và R – R’ trong mỗi trường hợp sau:
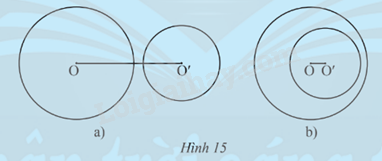
Trường hợp 1: (O;R) và (O’;R’) không có điểm chung (Hình 15).
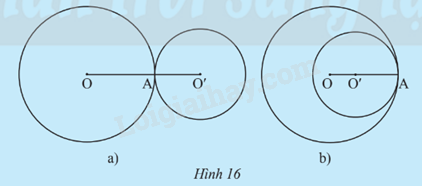
Trường hợp 2: (O;R) và (O’;R’) chỉ có 1 điểm chung (Hình 16).
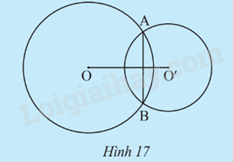
Trường hợp 3: (O;R) và (O’;R’) có đúng 2 điểm chung (Hình 17).
Phương pháp giải:
Nhìn vào hình để so sánh
Lời giải chi tiết:
Trường hợp 1: (O;R) và (O’;R’) không có điểm chung (Hình 15).
Hình 15a: OO’ > R + R’ ; OO’ > R – R’
Hình 15b: OO’ > R + R’; OO’ < R – R’
Trường hợp 2: (O;R) và (O’;R’) chỉ có 1 điểm chung (Hình 16).
Hình 16a: OO’ = R + R’ ; OO’ > R – R’
Hình 16b: OO’ < R + R’; OO’ = R – R’
Trường hợp 3: (O;R) và (O’;R’) có đúng 2 điểm chung (Hình 17).
OO’ < R + R’ ; OO’ > R – R’.
Video hướng dẫn giải
Trả lời câu hỏi Vận dụng 4 trang 81SGK Toán 9 Chân trời sáng tạo
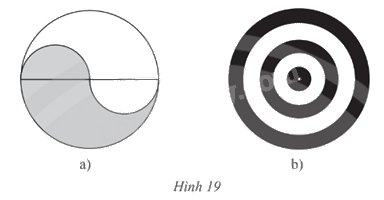
Dùng compa đo bán kính và vẽ lại các hình trong Hình 19.
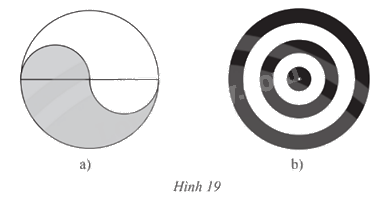
Phương pháp giải:
Dùng compa và tự vẽ lại các hình.
Lời giải chi tiết:
Hình 19.a)
- Đặt đầu nhọn vào tâm đường tròn lớn, mở cung của compa sao cho đầu bút nằm trên đường tròn lớn, vẽ lại vào vở được đường tròn lớn.
- Kẻ đường kính AB của đường tròn lớn
- Chia đường kính thành 4 đoạn thẳng bằng nhau.
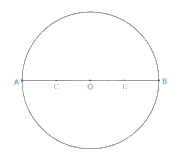
- Từ điểm C vẽ nửa đường tròn phía trên bán kính AC.
- Từ điểm D vẽ nửa đường tròn phía dưới bán kính DB.
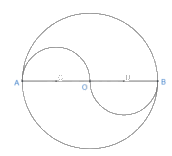
- Xóa tên các điểm vừa đặt, ta được hình 19.a.
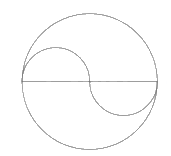
Em có thể tô thêm màu để giống hình trong sách nhé!
Hình 19.b)
Ta sẽ vẽ lần lượt các đường tròn theo thứ tự sau:
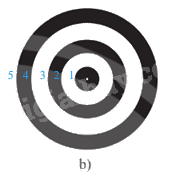
Các đường tròn này có cùng một tâm nên ta chỉ cần xác định 1 tâm để vẽ tất cả các đường tròn.
- Vẽ đường tròn 1: Đặt đầu nhọn vào tâm đường tròn trong sách, mở cung của compa sao cho đầu bút nằm trên đường tròn 1, vẽ lại vào vở được đường tròn 1.

- Vẽ đường tròn 2: Đặt đầu nhọn vào tâm đường tròn trong sách, mở cung của compa sao cho đầu bút nằm trên đường tròn 2, vẽ lại vào vở được đường tròn 2.

- Làm tương tự với đường tròn 3, 4, 5, như vậy ta có hình 19.b.
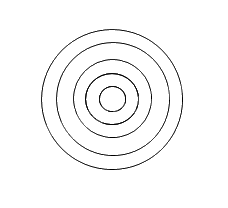
Em có thể tô thêm màu để giống hình trong sách nhé!
Video hướng dẫn giải
Trả lời câu hỏi Hoạt động 4 trang 78 SGK Toán 9 Chân trời sáng tạo
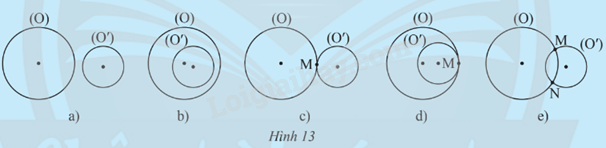
Tìm số điểm chung của hai đường tròn (O) và (O’) trong mỗi trường hợp sau:
Phương pháp giải:
Nhìn vào hình để xác định điểm chung của hai đường tròn.
Lời giải chi tiết:
a) Không có điểm chung
b) Không có điểm chung
c) Một điểm chung M
d) Một điểm chung M
e) Hai điểm chung M và N.
Video hướng dẫn giải
Trả lời câu hỏi Hoạt động 5 trang 79SGK Toán 9 Chân trời sáng tạo
Cho hai đường tròn phân biệt (O;R) và (O’;R’) với R \( \ge \) R’.
Hãy so sánh OO’ với R + R’ và R – R’ trong mỗi trường hợp sau:
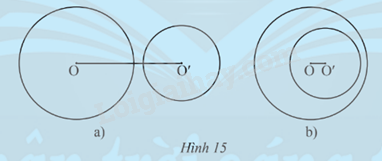
Trường hợp 1: (O;R) và (O’;R’) không có điểm chung (Hình 15).
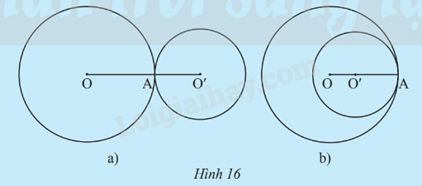
Trường hợp 2: (O;R) và (O’;R’) chỉ có 1 điểm chung (Hình 16).
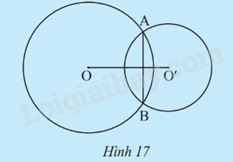
Trường hợp 3: (O;R) và (O’;R’) có đúng 2 điểm chung (Hình 17).
Phương pháp giải:
Nhìn vào hình để so sánh
Lời giải chi tiết:
Trường hợp 1: (O;R) và (O’;R’) không có điểm chung (Hình 15).
Hình 15a: OO’ > R + R’ ; OO’ > R – R’
Hình 15b: OO’ > R + R’; OO’ < R – R’
Trường hợp 2: (O;R) và (O’;R’) chỉ có 1 điểm chung (Hình 16).
Hình 16a: OO’ = R + R’ ; OO’ > R – R’
Hình 16b: OO’ < R + R’; OO’ = R – R’
Trường hợp 3: (O;R) và (O’;R’) có đúng 2 điểm chung (Hình 17).
OO’ < R + R’ ; OO’ > R – R’.
Video hướng dẫn giải
Trả lời câu hỏi Thực hành 3 trang 80 SGK Toán 9 Chân trời sáng tạo
Xác định vị trí tương đối giữa hai đường tròn (I;R) và (J;R’) trong mỗi trường hợp sau:
a) IJ = 5; R = 3; R’ = 2
b) IJ = 4; R = 11; R’ = 7
c) IJ = 6; R = 9; R’ = 4
d) IJ = 10; R = 4; R’ = 1
Phương pháp giải:
Dựa vào VD5 trang 80 làm tương tự.
Lời giải chi tiết:
a) Ta có 5 = 3 + 2 nên IJ = R + R’, suy ra hai đường tròn (I;R) và (J;R’) tiếp xúc ngoài.
b) Ta có 4 = 11 – 7 nên IJ = R - R’, suy ra hai đường tròn (I;R) và (J;R’) tiếp xúc trong.
c) Ta có 9 – 4 < 6 < 9 + 4 nên R - R’ < IJ < R + R’, suy ra hai đường tròn (I;R) và (J;R’) cắt nhau.
d) Ta có 10 > 4 + 1 nên IJ > R - R’, suy ra hai đường tròn (I;R) và (J;R’) ở ngoài nhau.
Video hướng dẫn giải
Trả lời câu hỏi Vận dụng 3 trang 81 SGK Toán 9 Chân trời sáng tạo
Mô tả vị trí tương đối giữa mỗi cặp đường tròn trong hình chụp bộ cồng chiêng Tây Nguyên trong Hình 18.

Phương pháp giải:
Dựa vào định nghĩa về vị trí tương đối của hai đường tròn để xác định.
Lời giải chi tiết:
a) Hai đường tròn không giao nhau
b) Hai đường tròn tiếp xúc nhau
c) Hai đường tròn cắt nhau.
Video hướng dẫn giải
Trả lời câu hỏi Vận dụng 4 trang 81SGK Toán 9 Chân trời sáng tạo
Dùng compa đo bán kính và vẽ lại các hình trong Hình 19.
Phương pháp giải:
Dùng compa và tự vẽ lại các hình.
Lời giải chi tiết:
Hình 19.a)
- Đặt đầu nhọn vào tâm đường tròn lớn, mở cung của compa sao cho đầu bút nằm trên đường tròn lớn, vẽ lại vào vở được đường tròn lớn.
- Kẻ đường kính AB của đường tròn lớn
- Chia đường kính thành 4 đoạn thẳng bằng nhau.
- Từ điểm C vẽ nửa đường tròn phía trên bán kính AC.
- Từ điểm D vẽ nửa đường tròn phía dưới bán kính DB.
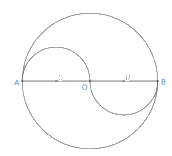
- Xóa tên các điểm vừa đặt, ta được hình 19.a.
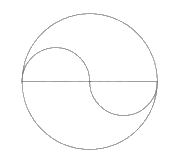
Em có thể tô thêm màu để giống hình trong sách nhé!
Hình 19.b)
Ta sẽ vẽ lần lượt các đường tròn theo thứ tự sau:
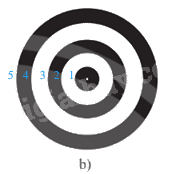
Các đường tròn này có cùng một tâm nên ta chỉ cần xác định 1 tâm để vẽ tất cả các đường tròn.
- Vẽ đường tròn 1: Đặt đầu nhọn vào tâm đường tròn trong sách, mở cung của compa sao cho đầu bút nằm trên đường tròn 1, vẽ lại vào vở được đường tròn 1.

- Vẽ đường tròn 2: Đặt đầu nhọn vào tâm đường tròn trong sách, mở cung của compa sao cho đầu bút nằm trên đường tròn 2, vẽ lại vào vở được đường tròn 2.

- Làm tương tự với đường tròn 3, 4, 5, như vậy ta có hình 19.b.
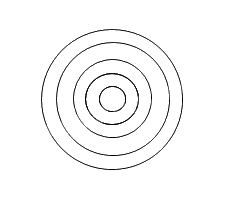
Em có thể tô thêm màu để giống hình trong sách nhé!
Mục 4 của chương trình Toán 9 tập 1 - Chân trời sáng tạo tập trung vào việc ôn tập và củng cố kiến thức về hàm số bậc nhất. Các bài tập trong mục này yêu cầu học sinh vận dụng các kiến thức đã học để giải quyết các bài toán thực tế, đồng thời rèn luyện kỹ năng tư duy logic và khả năng giải quyết vấn đề.
Bài 1 yêu cầu học sinh nhắc lại các khái niệm cơ bản về hàm số bậc nhất, bao gồm định nghĩa, dạng tổng quát, hệ số góc và giao điểm với các trục tọa độ. Đồng thời, học sinh cần biết cách xác định hàm số bậc nhất khi cho trước các yếu tố khác nhau.
Bài 2 tập trung vào việc xác định hàm số bậc nhất dựa trên các thông tin cho trước, chẳng hạn như đồ thị, hệ số góc và điểm thuộc đồ thị. Học sinh cần nắm vững các phương pháp xác định hàm số bậc nhất để giải quyết các bài toán một cách hiệu quả.
Bài 3 yêu cầu học sinh vẽ đồ thị của hàm số bậc nhất. Để vẽ đồ thị chính xác, học sinh cần xác định được các điểm đặc biệt trên đồ thị, chẳng hạn như giao điểm với các trục tọa độ. Ngoài ra, học sinh cần biết cách sử dụng các công cụ hỗ trợ để vẽ đồ thị một cách nhanh chóng và chính xác.
Bài 4 là bài tập vận dụng, yêu cầu học sinh sử dụng kiến thức về hàm số bậc nhất để giải quyết các bài toán thực tế. Các bài toán này thường liên quan đến các tình huống trong đời sống, chẳng hạn như tính quãng đường, thời gian, chi phí,...
Để giúp các em học sinh giải quyết các bài tập trong mục 4 một cách dễ dàng, giaitoan.edu.vn cung cấp lời giải chi tiết cho từng bài tập. Lời giải được trình bày rõ ràng, dễ hiểu, kèm theo các hình vẽ minh họa và các lưu ý quan trọng. Các em có thể tham khảo lời giải để hiểu rõ hơn về phương pháp giải và tự luyện tập để nâng cao kỹ năng.
Ngoài sách giáo khoa, các em có thể tham khảo thêm các tài liệu sau để học tốt môn Toán 9:
Hy vọng rằng với lời giải chi tiết và các hướng dẫn hữu ích, các em học sinh sẽ tự tin hơn trong việc giải các bài tập trong mục 4 trang 78, 79, 80 SGK Toán 9 tập 1 - Chân trời sáng tạo. Chúc các em học tập tốt!