Giaitoan.edu.vn xin giới thiệu lời giải chi tiết mục 3 trang 72 SGK Toán 9 tập 2 - Chân trời sáng tạo. Bài giải được trình bày rõ ràng, dễ hiểu, giúp học sinh nắm vững kiến thức và rèn luyện kỹ năng giải toán.
Chúng tôi luôn cập nhật nhanh chóng và chính xác các lời giải bài tập Toán 9, đáp ứng nhu cầu học tập của học sinh trên toàn quốc.
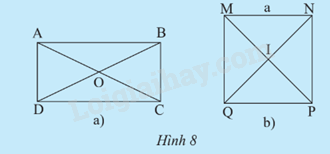
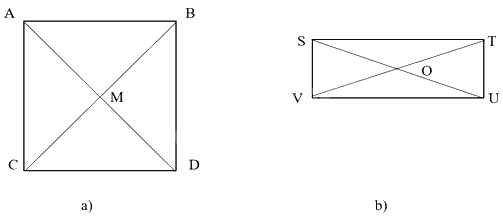
a) Gọi O là giao điểm của hai đường chéo AC và BD. So sánh độ dài các đoạn thẳng OA, OB, OC, OD. Nêu nhận xét về tâm và đường kính của đường tròn ngoại tiếp hình chữ nhật ABCD. b) Xác định tâm và bán kính của đường tròn ngoại tiếp hình vuông MNPQ có cạnh bằng a.
Video hướng dẫn giải
Trả lời câu hỏi Hoạt động 3 trang 72SGK Toán 9 Chân trời sáng tạo
a) Gọi O là giao điểm của hai đường chéo AC và BD. So sánh độ dài các đoạn thẳng OA, OB, OC, OD. Nêu nhận xét về tâm và đường kính của đường tròn ngoại tiếp hình chữ nhật ABCD.
b) Xác định tâm và bán kính của đường tròn ngoại tiếp hình vuông MNPQ có cạnh bằng a.
Phương pháp giải:
Dựa vào: Trong hình chữ nhật, hai đường chéo bằng nhau và cắt nhau tại trung điểm mỗi đường.
Lời giải chi tiết:
a) Độ dài các đoạn thẳng OA, OB, OC, OD là bằng nhau.
Nhận xét:
+ Tâm của đường tròn ngoại tiếp hình chữ nhật ABCD là giao điểm của hai đường chéo.
+ Đường kính của đường tròn ngoại tiếp hình chữ nhật ABCD là đường chéo của hình chữ nhật.
b) Tâm của đường tròn ngoại tiếp hình vuông MNPQ là I.
Bán kính của đường tròn ngoại tiếp hình vuông MNPQ bằng một nửa cạnh huyền.
Đường chéo của hình vuông là: \(\sqrt {a^2 + a^2} = a\sqrt 2\)
Bán kính của đường tròn ngoại tiếp hình vuông MNPQ là:
R = IM = IN = IP = IQ = \(\frac{{{a\sqrt 2}}}{2}\).
Video hướng dẫn giải
Trả lời câu hỏi Vận dụng 3 trang 73 SGK Toán 9 Chân trời sáng tạo
Một người muốn thiết kế một bảng hiệu gồm một hình vuông nội tiếp một đường tròn bán kính R = 3 cm (Hình 12). Tính diện tích hình vuông đó.

Phương pháp giải:
Dựa vào: Đường tròn ngoại tiếp hình chữ nhật, hình vuông có tâm là giao điểm của hai đường chéo và có bán kính bằng nửa đường chéo.
Lời giải chi tiết:
Ta thấy đường tròn ngoại tiếp hình vuông suy ra độ dài đường chéo hình vuông là đường kính của hình tròn.
Độ dài của đường chéo hình vuông là: d = 2.R = 2.3 = 6 cm.
Độ dài cạnh hình vuông là: a = \(\sqrt {\frac{{{d^2}}}{2}} = \sqrt {\frac{{{6^2}}}{2}} = 3\sqrt 2 \) cm.
Diện tích hình vuông là: \(3\sqrt 2 .3\sqrt 2 \) = 18 (cm2).
Video hướng dẫn giải
Trả lời câu hỏi Hoạt động 3 trang 72SGK Toán 9 Chân trời sáng tạo
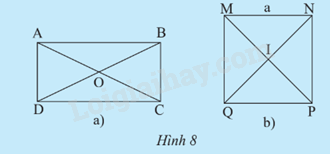
a) Gọi O là giao điểm của hai đường chéo AC và BD. So sánh độ dài các đoạn thẳng OA, OB, OC, OD. Nêu nhận xét về tâm và đường kính của đường tròn ngoại tiếp hình chữ nhật ABCD.
b) Xác định tâm và bán kính của đường tròn ngoại tiếp hình vuông MNPQ có cạnh bằng a.
Phương pháp giải:
Dựa vào: Trong hình chữ nhật, hai đường chéo bằng nhau và cắt nhau tại trung điểm mỗi đường.
Lời giải chi tiết:
a) Độ dài các đoạn thẳng OA, OB, OC, OD là bằng nhau.
Nhận xét:
+ Tâm của đường tròn ngoại tiếp hình chữ nhật ABCD là giao điểm của hai đường chéo.
+ Đường kính của đường tròn ngoại tiếp hình chữ nhật ABCD là đường chéo của hình chữ nhật.
b) Tâm của đường tròn ngoại tiếp hình vuông MNPQ là I.
Bán kính của đường tròn ngoại tiếp hình vuông MNPQ bằng một nửa cạnh huyền.
Đường chéo của hình vuông là: \(\sqrt {a^2 + a^2} = a\sqrt 2\)
Bán kính của đường tròn ngoại tiếp hình vuông MNPQ là:
R = IM = IN = IP = IQ = \(\frac{{{a\sqrt 2}}}{2}\).
Video hướng dẫn giải
Trả lời câu hỏi Thực hành 3 trang 73 SGK Toán 9 Chân trời sáng tạo
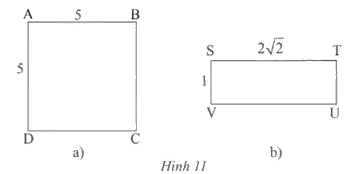
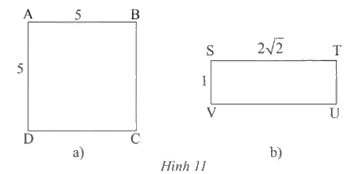
Xác định tâm và bán kính của đường tròn ngoại tiếp hình vuông và hình chữ nhật trong Hình 11.
Phương pháp giải:
Dựa vào: Đường tròn ngoại tiếp hình chữ nhật, hình vuông có tâm là giao điểm của hai đường chéo và có bán kính bằng nửa đường chéo.
Lời giải chi tiết:
a) Hình vuông ABCD có M là giao điểm của hai đường chéo. Suy ra đường tròn ngoại tiếp hình vuông ABCD có tâm M và bán kính R = \(\frac{{a\sqrt 2 }}{2} = \frac{{5\sqrt 2 }}{2}\).
b) Hình chữ nhật STUV có O là giao điểm của hai đường chéo. Suy ra đường tròn ngoại tiếp hình chữ nhật STUV có tâm O và bán kính
R = \(\frac{{SU}}{2} = \frac{{\sqrt {S{T^2} + U{T^2}} }}{2} = \frac{{\sqrt {{{\left( {2\sqrt 2 } \right)}^2} + {1^2}} }}{2} = \frac{{\sqrt 9 }}{2} = \frac{3}{2}\).
Video hướng dẫn giải
Trả lời câu hỏi Vận dụng 3 trang 73 SGK Toán 9 Chân trời sáng tạo
Một người muốn thiết kế một bảng hiệu gồm một hình vuông nội tiếp một đường tròn bán kính R = 3 cm (Hình 12). Tính diện tích hình vuông đó.

Phương pháp giải:
Dựa vào: Đường tròn ngoại tiếp hình chữ nhật, hình vuông có tâm là giao điểm của hai đường chéo và có bán kính bằng nửa đường chéo.
Lời giải chi tiết:
Ta thấy đường tròn ngoại tiếp hình vuông suy ra độ dài đường chéo hình vuông là đường kính của hình tròn.
Độ dài của đường chéo hình vuông là: d = 2.R = 2.3 = 6 cm.
Độ dài cạnh hình vuông là: a = \(\sqrt {\frac{{{d^2}}}{2}} = \sqrt {\frac{{{6^2}}}{2}} = 3\sqrt 2 \) cm.
Diện tích hình vuông là: \(3\sqrt 2 .3\sqrt 2 \) = 18 (cm2).
Video hướng dẫn giải
Trả lời câu hỏi Thực hành 3 trang 73 SGK Toán 9 Chân trời sáng tạo
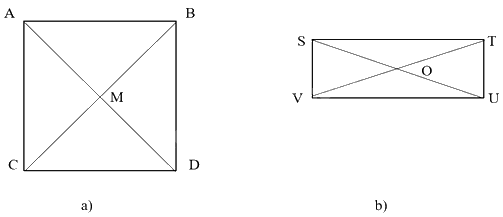
Xác định tâm và bán kính của đường tròn ngoại tiếp hình vuông và hình chữ nhật trong Hình 11.
Phương pháp giải:
Dựa vào: Đường tròn ngoại tiếp hình chữ nhật, hình vuông có tâm là giao điểm của hai đường chéo và có bán kính bằng nửa đường chéo.
Lời giải chi tiết:
a) Hình vuông ABCD có M là giao điểm của hai đường chéo. Suy ra đường tròn ngoại tiếp hình vuông ABCD có tâm M và bán kính R = \(\frac{{a\sqrt 2 }}{2} = \frac{{5\sqrt 2 }}{2}\).
b) Hình chữ nhật STUV có O là giao điểm của hai đường chéo. Suy ra đường tròn ngoại tiếp hình chữ nhật STUV có tâm O và bán kính
R = \(\frac{{SU}}{2} = \frac{{\sqrt {S{T^2} + U{T^2}} }}{2} = \frac{{\sqrt {{{\left( {2\sqrt 2 } \right)}^2} + {1^2}} }}{2} = \frac{{\sqrt 9 }}{2} = \frac{3}{2}\).
Mục 3 trang 72 SGK Toán 9 tập 2 - Chân trời sáng tạo thường xoay quanh các bài toán liên quan đến hàm số bậc hai, bao gồm việc xác định hệ số, tìm đỉnh parabol, vẽ đồ thị hàm số và ứng dụng vào giải quyết các bài toán thực tế. Việc nắm vững kiến thức về hàm số bậc hai là nền tảng quan trọng cho các chương trình học toán ở các lớp trên.
Bài học này tập trung vào việc củng cố kiến thức về:
Để giải quyết hiệu quả các bài toán trong mục này, học sinh cần nắm vững các phương pháp sau:
Bài tập: Cho hàm số y = 2x2 - 4x + 1. Hãy tìm tọa độ đỉnh của parabol.
Giải:
Hàm số có dạng y = ax2 + bx + c, với a = 2, b = -4, c = 1.
Tọa độ đỉnh của parabol là:
xđỉnh = -b / (2a) = -(-4) / (2 * 2) = 1
yđỉnh = 2 * (1)2 - 4 * (1) + 1 = -1
Vậy tọa độ đỉnh của parabol là (1; -1).
Để nắm vững kiến thức và kỹ năng giải toán trong Mục 3 trang 72 SGK Toán 9 tập 2 - Chân trời sáng tạo, học sinh nên:
Ngoài việc giải các bài tập trong SGK, học sinh có thể tìm hiểu thêm về:
Mục 3 trang 72 SGK Toán 9 tập 2 - Chân trời sáng tạo là một phần quan trọng trong chương trình học Toán 9. Việc nắm vững kiến thức và kỹ năng giải toán trong mục này sẽ giúp học sinh tự tin hơn trong các kỳ thi và chuẩn bị tốt cho các chương trình học toán ở các lớp trên. Giaitoan.edu.vn hy vọng rằng với lời giải chi tiết và phương pháp giải hiệu quả, học sinh sẽ học tập tốt môn Toán 9.