Chào mừng các em học sinh đến với chuyên mục giải bài tập Toán 9 tập 2 của giaitoan.edu.vn. Ở bài viết này, chúng tôi sẽ cung cấp lời giải chi tiết và dễ hiểu cho các bài tập trong mục 1 trang 88 và 89 sách giáo khoa Toán 9 tập 2 - Chân trời sáng tạo.
Mục tiêu của chúng tôi là giúp các em nắm vững kiến thức, rèn luyện kỹ năng giải toán và đạt kết quả tốt nhất trong học tập.
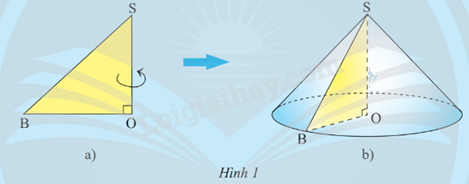
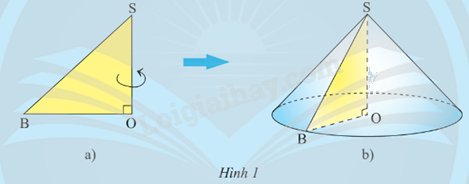
Cho tấm bìa có dạng hình tam giác OSB vuông tại O, cạnh SO cố định (Hình 1a). Khi quay tấm bìa một vòng quanh cạnh SO thì hình tạo ra giống với đồ vật quen thuộc nào?
Video hướng dẫn giải
Trả lời câu hỏi Thực hành 2 trang 89SGK Toán 9 Chân trời sáng tạo
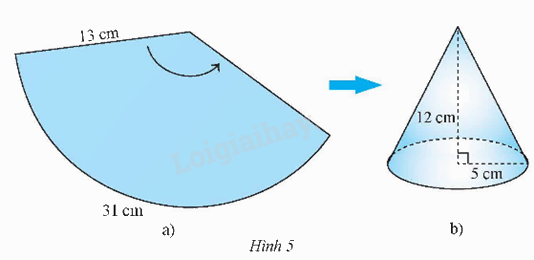
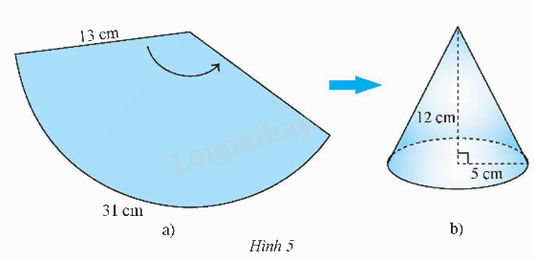
Tạo lập hình nón có chiều cao 12 cm và bán kính đáy 5 cm theo hướng dẫn sau:
- Cắt tấm bìa hình quạt tròn có bán kính bằng độ dài đường sinh l = \(\sqrt {{5^2} + {{12}^2}} \) = 13 (cm), độ dài cung của hình quạt tròn bằng 10\(\pi \)cm \( \approx \) 31 cm (Hình 5a).
- Cắt tấm bìa hình tròn bán kính 5 cm.
- Ghép và dán hai mép quạt lại với nhau sao cho cung của nó tạo thành đường tròn, rồi dán tấm bìa hình tròn ở trên vào làm đáy, ta được hình nón như Hình 5b.
Phương pháp giải:
Dựa vào dữ kiện đề bài và làm theo.
Lời giải chi tiết:
Lấy giấy làm thủ công tương tự các bước như ở trên.
Video hướng dẫn giải
Trả lời câu hỏi Hoạt động 1 trang 88 SGK Toán 9 Chân trời sáng tạo
Cho tấm bìa có dạng hình tam giác OSB vuông tại O, cạnh SO cố định (Hình 1a). Khi quay tấm bìa một vòng quanh cạnh SO thì hình tạo ra giống với đồ vật quen thuộc nào?
Phương pháp giải:
Tìm các vật thực tế.
Lời giải chi tiết:
Hình tạo ra giống đồ vật như: hình nón lá, mũ đội sinh nhật,...
Video hướng dẫn giải
Trả lời câu hỏi Thực hành 1 trang 89SGK Toán 9 Chân trời sáng tạo
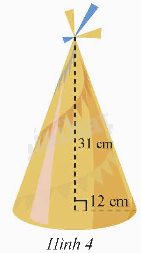
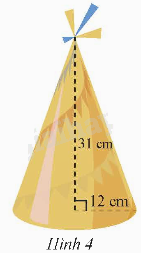
Chiếc mũ ở Hình 4 có dạng hình nón. Cho biết bán kính đáy, chiều cao và độ dài đường sinh của hình nón đó.
Phương pháp giải:
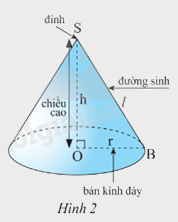
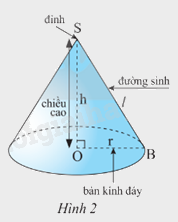
Dựa vào: Khi quay một tam giác vuông SOB một vòng quanh cạnh góc vuông SO cố định ta được một hình nón.
+ S gọi là đỉnh của hình nón
+ Cạnh OB quét thành hình tròn gọi là đấy của hình nón. Bán kính của đáy gọi là bán kính đáy của hình nón.
+ Cạnh SB quét thành mặt xung quanh của hình nón. Mỗi vị trí của SB là một đường sinh.
+ Độ dài SO là chiều cao hình nón.
Lời giải chi tiết:
Bán kính đáy có độ dài 12 cm.
Chiều cao là 31 cm.
Độ dài đường sinh là: l = \(\sqrt {{{12}^2} + {{31}^2}} = \sqrt {1105} \) (cm).
Video hướng dẫn giải
Trả lời câu hỏi Hoạt động 1 trang 88 SGK Toán 9 Chân trời sáng tạo
Cho tấm bìa có dạng hình tam giác OSB vuông tại O, cạnh SO cố định (Hình 1a). Khi quay tấm bìa một vòng quanh cạnh SO thì hình tạo ra giống với đồ vật quen thuộc nào?
Phương pháp giải:
Tìm các vật thực tế.
Lời giải chi tiết:
Hình tạo ra giống đồ vật như: hình nón lá, mũ đội sinh nhật,...
Video hướng dẫn giải
Trả lời câu hỏi Thực hành 1 trang 89SGK Toán 9 Chân trời sáng tạo
Chiếc mũ ở Hình 4 có dạng hình nón. Cho biết bán kính đáy, chiều cao và độ dài đường sinh của hình nón đó.
Phương pháp giải:
Dựa vào: Khi quay một tam giác vuông SOB một vòng quanh cạnh góc vuông SO cố định ta được một hình nón.
+ S gọi là đỉnh của hình nón
+ Cạnh OB quét thành hình tròn gọi là đấy của hình nón. Bán kính của đáy gọi là bán kính đáy của hình nón.
+ Cạnh SB quét thành mặt xung quanh của hình nón. Mỗi vị trí của SB là một đường sinh.
+ Độ dài SO là chiều cao hình nón.
Lời giải chi tiết:
Bán kính đáy có độ dài 12 cm.
Chiều cao là 31 cm.
Độ dài đường sinh là: l = \(\sqrt {{{12}^2} + {{31}^2}} = \sqrt {1105} \) (cm).
Video hướng dẫn giải
Trả lời câu hỏi Thực hành 2 trang 89SGK Toán 9 Chân trời sáng tạo
Tạo lập hình nón có chiều cao 12 cm và bán kính đáy 5 cm theo hướng dẫn sau:
- Cắt tấm bìa hình quạt tròn có bán kính bằng độ dài đường sinh l = \(\sqrt {{5^2} + {{12}^2}} \) = 13 (cm), độ dài cung của hình quạt tròn bằng 10\(\pi \)cm \( \approx \) 31 cm (Hình 5a).
- Cắt tấm bìa hình tròn bán kính 5 cm.
- Ghép và dán hai mép quạt lại với nhau sao cho cung của nó tạo thành đường tròn, rồi dán tấm bìa hình tròn ở trên vào làm đáy, ta được hình nón như Hình 5b.
Phương pháp giải:
Dựa vào dữ kiện đề bài và làm theo.
Lời giải chi tiết:
Lấy giấy làm thủ công tương tự các bước như ở trên.
Mục 1 của chương trình Toán 9 tập 2 - Chân trời sáng tạo tập trung vào việc ôn tập và hệ thống hóa kiến thức về hàm số bậc hai. Các bài tập trong trang 88 và 89 SGK Toán 9 tập 2 yêu cầu học sinh vận dụng các kiến thức đã học để giải quyết các bài toán thực tế, rèn luyện tư duy logic và kỹ năng giải toán.
Bài 1 yêu cầu học sinh xác định các hệ số a, b, c của hàm số bậc hai, tìm tọa độ đỉnh của parabol, vẽ đồ thị hàm số và xác định khoảng đồng biến, nghịch biến của hàm số. Để giải bài tập này, học sinh cần nắm vững các công thức và tính chất của hàm số bậc hai.
Bài 2 thường đưa ra các bài toán thực tế liên quan đến quỹ đạo chuyển động của vật, diện tích hình chữ nhật, hoặc các bài toán tối ưu hóa. Để giải quyết các bài toán này, học sinh cần xây dựng được hàm số bậc hai mô tả mối quan hệ giữa các đại lượng trong bài toán, sau đó tìm giá trị lớn nhất hoặc nhỏ nhất của hàm số.
Bài 3 thường là các câu hỏi trắc nghiệm nhằm kiểm tra khả năng nắm vững kiến thức và kỹ năng giải toán của học sinh. Để làm tốt bài tập trắc nghiệm, học sinh cần đọc kỹ đề bài, phân tích các phương án trả lời và lựa chọn phương án đúng nhất.
Để giải bài tập Toán 9 tập 2 - Chân trời sáng tạo một cách hiệu quả, học sinh cần:
Hy vọng với lời giải chi tiết và những lời khuyên trên, các em học sinh sẽ tự tin hơn khi giải các bài tập trong mục 1 trang 88, 89 SGK Toán 9 tập 2 - Chân trời sáng tạo. Chúc các em học tập tốt!