Giải bài tập 2 trang 69 SGK Toán 9 tập 2 - Chân trời sáng tạo

Giaitoan.edu.vn xin giới thiệu lời giải chi tiết bài tập 2 trang 69 SGK Toán 9 tập 2 - Chân trời sáng tạo. Bài viết này sẽ giúp học sinh nắm vững kiến thức, hiểu rõ phương pháp giải và tự tin làm bài tập.

Chúng tôi cung cấp đáp án chính xác, dễ hiểu cùng với các bước giải cụ thể, giúp bạn học Toán 9 một cách hiệu quả nhất.

Cho tam giác ABC ( AC < BC) nội tiếp đường tròn (O) có AB là đường kính. Từ điểm O vẽ đường thẳng song song với AC và cắt đường tròn (O) tại I (điểm I thuộc cung nhỏ CB). a) Chứng minh OI vuông góc với BC. b) Vẽ tiếp tuyến của đường tròn (O) tại B và cắt OI tại M. Chứng minh MC là tiếp tuyến của đường tròn (O).

Đề bài

Cho tam giác ABC ( AC < BC) nội tiếp đường tròn (O) có AB là đường kính. Từ điểm O vẽ đường thẳng song song với AC và cắt đường tròn (O) tại I (điểm I thuộc cung nhỏ CB).

a) Chứng minh OI vuông góc với BC.

b) Vẽ tiếp tuyến của đường tròn (O) tại B và cắt OI tại M. Chứng minh MC là tiếp tuyến của đường tròn (O).

Video hướng dẫn giải

Phương pháp giải - Xem chi tiết Giải bài tập 2 trang 69 SGK Toán 9 tập 2 - Chân trời sáng tạo 1

- Đọc kĩ dữ kiện đề bài để vẽ hình.

- Chứng minh tam giác ABC vuông tại C và OI // AC để suy ra OI vuông góc với BC.

- Chứng minh \(\Delta \)COM = \(\Delta \)BOM (c – g – c) nên \(\widehat {OBM} = \widehat {OCM} = {90^o}\)

Suy ra MC là tiếp tuyến đường tròn (O).

Lời giải chi tiết

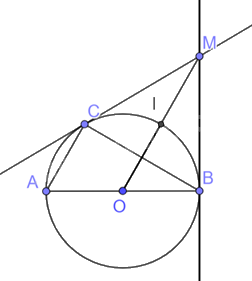
Giải bài tập 2 trang 69 SGK Toán 9 tập 2 - Chân trời sáng tạo 2

a) Xét đường tròn (O) có:

\(\widehat {ACB}\) là góc nội tiếp chắn cung AB, mà AB là đường kính của đường tròn (O).

\(\widehat {ACB}\) = 90^o hay tam giác ABC vuông tại C, mà OI // AC (giả thiết).

Suy ra OI \( \bot \) BC (quan hệ từ vuông góc – song song).

b) Vì OB = OC = R suy ra tam giác OBC cân tại O mà OI là đường cao của tam giác OBC.

Suy ra OI đồng thời là phân giác của tam giác OBC.

Suy ra \(\widehat {COI} = \widehat {BOI}\) hay \(\widehat {COM} = \widehat {BOM}\)

Xét \(\Delta \) COM và \(\Delta \) BOM có:

OC = OB = R;

\(\widehat {COM} = \widehat {BOM}\) (chứng minh trên);

OM chung.

Suy ra \(\Delta \)COM = \(\Delta \)BOM (c – g – c).

Do đó, \(\widehat {OBM} = \widehat {OCM}\) (hai góc tương ứng)

Mà \(\widehat {OBM}\) = 90^o (do MB là tiếp tuyến của đường tròn).

Suy ra \(\widehat {OCM}\) = 90^o hay OM \( \bot \) MC mà C thuộc đường tròn (O)

Suy ra MC là tiếp tuyến đường tròn (O).

Làm chủ Toán 9, tự tin vào phòng thi! Đừng bỏ lỡ Giải bài tập 2 trang 69 SGK Toán 9 tập 2 - Chân trời sáng tạo đặc sắc thuộc chuyên mục toán lớp 9 trên nền tảng tài liệu toán. Với bộ bài tập lý thuyết toán thcs được biên soạn chuyên sâu, bám sát cấu trúc đề thi và chương trình sách giáo khoa mới nhất, đây chính là công cụ đắc lực giúp các em tối ưu hóa ôn luyện, củng cố kiến thức vững chắc và thuần thục mọi dạng bài thi khó nhằn. Phương pháp học trực quan, khoa học sẽ mang lại hiệu quả vượt trội, giúp con bạn chinh phục mọi thử thách một cách dễ dàng.

Giải bài tập 2 trang 69 SGK Toán 9 tập 2 - Chân trời sáng tạo: Hướng dẫn chi tiết

Bài tập 2 trang 69 SGK Toán 9 tập 2 - Chân trời sáng tạo thuộc chương trình học Toán 9, tập trung vào việc vận dụng các kiến thức về hàm số bậc hai để giải quyết các bài toán thực tế. Để giải quyết bài tập này một cách hiệu quả, học sinh cần nắm vững các khái niệm cơ bản như:

Hàm số bậc hai là gì?
Cách xác định các hệ số a, b, c trong hàm số bậc hai y = ax² + bx + c.
Cách tìm tập xác định của hàm số bậc hai.
Cách vẽ đồ thị hàm số bậc hai.

Phân tích đề bài và tìm hướng giải

Trước khi bắt tay vào giải bài tập, học sinh cần đọc kỹ đề bài, xác định rõ yêu cầu của bài toán và tìm ra hướng giải phù hợp. Trong bài tập 2 trang 69, yêu cầu thường là tìm các thông số của hàm số bậc hai dựa trên các điều kiện cho trước hoặc xác định các điểm thuộc đồ thị hàm số.

Lời giải chi tiết bài tập 2 trang 69

Để giúp học sinh hiểu rõ hơn về cách giải bài tập này, chúng tôi sẽ trình bày lời giải chi tiết cho từng phần của bài tập. (Nội dung lời giải chi tiết sẽ được trình bày ở đây, bao gồm các bước giải, công thức sử dụng và giải thích rõ ràng từng bước. Ví dụ:)

Ví dụ: Giả sử đề bài yêu cầu tìm hệ số a của hàm số y = ax² + bx + c biết rằng đồ thị hàm số đi qua điểm A(1; 2) và có trục đối xứng là x = -1.

Bước 1: Thay tọa độ điểm A(1; 2) vào phương trình hàm số, ta được: 2 = a(1)² + b(1) + c => a + b + c = 2.
Bước 2: Sử dụng công thức trục đối xứng x = -b/2a, ta có: -1 = -b/2a => b = 2a.
Bước 3: Thay b = 2a vào phương trình a + b + c = 2, ta được: a + 2a + c = 2 => 3a + c = 2 => c = 2 - 3a.
Bước 4: (Tiếp tục các bước giải để tìm ra giá trị của a, b, c.)

Lưu ý khi giải bài tập

Trong quá trình giải bài tập, học sinh cần lưu ý một số điểm sau:

Đọc kỹ đề bài và xác định rõ yêu cầu của bài toán.
Sử dụng đúng các công thức và định lý đã học.
Kiểm tra lại kết quả sau khi giải xong.
Luyện tập thường xuyên để nắm vững kiến thức và kỹ năng giải bài tập.

Ứng dụng của hàm số bậc hai trong thực tế

Hàm số bậc hai có rất nhiều ứng dụng trong thực tế, ví dụ như:

Tính quỹ đạo của vật ném.
Xác định hình dạng của các vật thể parabol.
Giải quyết các bài toán tối ưu hóa.

Tổng kết

Bài tập 2 trang 69 SGK Toán 9 tập 2 - Chân trời sáng tạo là một bài tập quan trọng giúp học sinh củng cố kiến thức về hàm số bậc hai. Hy vọng với lời giải chi tiết và những lưu ý trên, các em học sinh sẽ tự tin hơn khi giải bài tập này và đạt kết quả tốt trong môn Toán 9.

Giaitoan.edu.vn luôn đồng hành cùng các em trên con đường chinh phục môn Toán. Chúc các em học tập tốt!