Chào mừng bạn đến với giaitoan.edu.vn, nơi cung cấp lời giải chi tiết và dễ hiểu cho các bài tập Toán 9 tập 1 - Chân trời sáng tạo. Bài viết này sẽ giúp bạn nắm vững kiến thức và kỹ năng giải bài tập 11 trang 104 một cách hiệu quả.
Chúng tôi hiểu rằng việc tự học Toán đôi khi gặp nhiều khó khăn. Vì vậy, đội ngũ giáo viên giàu kinh nghiệm của giaitoan.edu.vn đã biên soạn lời giải chi tiết, kèm theo các bước giải rõ ràng, giúp bạn dễ dàng tiếp thu và áp dụng vào các bài tập tương tự.
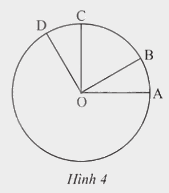
Quan sát Hình 4. Biết (widehat {DOA} = {120^o}), OA ( bot )OC, OB ( bot )OD. a) Đọc tên các góc ở tâm có trong hình. b) Tính số đo của mỗi góc ở tâm tìm được ở câu a c) Tìm các cặp cung bằng nhau và có số đo nhỏ hơn 180o d) So sánh hai cung nhỏ (oversetfrown{AB}) và (oversetfrown{CD}).
Đề bài
Quan sát Hình 4. Biết \(\widehat {DOA} = {120^o}\), OA \( \bot \)OC, OB \( \bot \)OD.
a) Đọc tên các góc ở tâm có trong hình.
b) Tính số đo của mỗi góc ở tâm tìm được ở câu a
c) Tìm các cặp cung bằng nhau và có số đo nhỏ hơn 180o
d) So sánh hai cung nhỏ \(\overset\frown{AB}\) và \(\overset\frown{CD}\).
Video hướng dẫn giải
Phương pháp giải - Xem chi tiết
Dựa vào: Góc ở tâm là góc có đỉnh trùng với tâm đường tròn, dựa vào hình để xác định góc.
Lời giải chi tiết
a) Các góc ở tâm có trong hình là: \(\widehat {DOA};\widehat {DOC};\widehat {COB};\widehat {BOA};\widehat {DOB};\widehat {COA}\)
b) Ta có: \(\widehat {DOA} = {120^o}\)
Vì \(OA \bot OC\) nên \(\widehat {COA} = {90^o}\)
Vì \(OB \bot OD\) nên \(\widehat {DOB} = {90^o}\)
Từ đó ta tính được:
\(\widehat {DOC} = \widehat {DOA} - \widehat {COA} = {120^o} - {90^o} = {30^o}\)
\(\widehat {COB} = \widehat {DOB} - \widehat {DOC} = {90^o} - {30^o} = {60^o}\)
\(\widehat {BOA} = \widehat {COA} - \widehat {COB} = {90^o} - {60^o} = {30^o}\)
c) sđ\(\overset\frown{CD}=\) sđ\(\overset\frown{AB}\) \((= 30^o)\)
sđ\(\overset\frown{BD}=\) sđ\(\overset\frown{AC}\) \(( = 90^o)\)
d) sđ\(\overset\frown{AB}\) = sđ\(\overset\frown{CD}\) \((=30^o)\)
Bài tập 11 trang 104 SGK Toán 9 tập 1 - Chân trời sáng tạo thuộc chương trình học về hàm số bậc nhất. Để giải bài tập này, học sinh cần nắm vững các kiến thức cơ bản về hàm số, cách xác định hệ số góc và tung độ gốc, cũng như các tính chất của hàm số.
Bài tập 11 yêu cầu học sinh xác định hệ số góc của đường thẳng trong các trường hợp cụ thể. Để làm được điều này, học sinh cần biến đổi phương trình đường thẳng về dạng y = ax + b, trong đó 'a' là hệ số góc.
Ví dụ 1: Xác định hệ số góc của đường thẳng có phương trình 2x + 3y = 6.
Giải:
Ví dụ 2: Xác định hệ số góc của đường thẳng có phương trình x - y = 5.
Giải:
Hàm số bậc nhất có dạng y = ax + b, trong đó 'a' là hệ số góc và 'b' là tung độ gốc. Hệ số góc 'a' quyết định độ dốc của đường thẳng. Nếu a > 0, đường thẳng đi lên từ trái sang phải. Nếu a < 0, đường thẳng đi xuống từ trái sang phải. Nếu a = 0, đường thẳng là đường thẳng ngang.
Để củng cố kiến thức về hàm số bậc nhất và rèn luyện kỹ năng giải bài tập, bạn có thể tham khảo thêm các bài tập sau:
Bài tập 11 trang 104 SGK Toán 9 tập 1 - Chân trời sáng tạo là một bài tập quan trọng giúp học sinh hiểu rõ hơn về hàm số bậc nhất và cách xác định hệ số góc. Hy vọng với hướng dẫn chi tiết và dễ hiểu trên, bạn sẽ tự tin giải bài tập này và đạt kết quả tốt trong môn Toán.