Bài tập 13 trang 105 SGK Toán 9 tập 1 - Chân trời sáng tạo là một phần quan trọng trong chương trình học Toán 9. Bài tập này giúp học sinh rèn luyện kỹ năng giải quyết các bài toán thực tế liên quan đến hàm số bậc nhất và ứng dụng của nó.
Giaitoan.edu.vn xin giới thiệu lời giải chi tiết, dễ hiểu bài tập 13 trang 105 SGK Toán 9 tập 1 - Chân trời sáng tạo, giúp các em học sinh nắm vững kiến thức và tự tin hơn trong quá trình học tập.
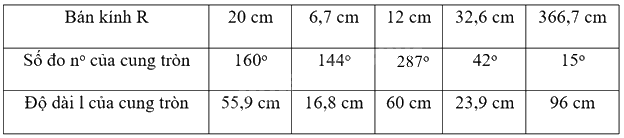
Hãy hoàn thành bảng số liệu sau và vở (lấy (pi approx 3,14) và làm tròn kết quả đến hàng phần mười)
Đề bài
Hãy hoàn thành bảng số liệu sau và vở (lấy \(\pi \approx 3,14\) và làm tròn kết quả đến hàng phần mười)

Video hướng dẫn giải
Phương pháp giải - Xem chi tiết
Dựa vào công thức: \(l = \frac{{\pi Rn}}{{180}}\)
Lời giải chi tiết
Bài tập 13 trang 105 SGK Toán 9 tập 1 - Chân trời sáng tạo yêu cầu học sinh vận dụng kiến thức về hàm số bậc nhất để giải quyết một bài toán thực tế. Để giải bài tập này một cách hiệu quả, chúng ta cần nắm vững các khái niệm cơ bản về hàm số bậc nhất, bao gồm:
Trước khi đi vào giải bài tập, chúng ta cần phân tích kỹ đề bài để xác định rõ các yếu tố quan trọng. Bài tập 13 thường liên quan đến việc xác định phương trình đường thẳng đi qua hai điểm cho trước, hoặc tìm giao điểm của hai đường thẳng.
Dưới đây là lời giải chi tiết bài tập 13 trang 105 SGK Toán 9 tập 1 - Chân trời sáng tạo:
(Nội dung lời giải chi tiết bài tập 13 sẽ được trình bày tại đây, bao gồm các bước giải, công thức sử dụng và kết quả cuối cùng. Ví dụ:)
Để giúp các em hiểu rõ hơn về cách giải bài tập này, chúng ta hãy xem xét một ví dụ minh họa:
Ví dụ: Tìm phương trình đường thẳng đi qua hai điểm A(1; 2) và B(3; 4).
Giải:
Để củng cố kiến thức và kỹ năng giải bài tập về hàm số bậc nhất, các em có thể luyện tập thêm với các bài tập sau:
Bài tập 13 trang 105 SGK Toán 9 tập 1 - Chân trời sáng tạo là một bài tập quan trọng giúp học sinh rèn luyện kỹ năng giải quyết các bài toán thực tế liên quan đến hàm số bậc nhất. Hy vọng với lời giải chi tiết và ví dụ minh họa trên, các em học sinh sẽ nắm vững kiến thức và tự tin hơn trong quá trình học tập.
| Công thức | Mô tả |
|---|---|
| y = ax + b | Phương trình hàm số bậc nhất |
| m = (y2 - y1) / (x2 - x1) | Công thức tính độ dốc của đường thẳng |
| y - y1 = m(x - x1) | Phương trình đường thẳng đi qua điểm A(x1; y1) và có độ dốc m |