Giaitoan.edu.vn xin giới thiệu lời giải chi tiết mục 3 trang 44 SGK Toán 9 tập 1 - Chân trời sáng tạo. Bài viết này cung cấp đáp án đầy đủ, phương pháp giải rõ ràng, giúp học sinh nắm vững kiến thức và tự tin làm bài tập.
Chúng tôi luôn cập nhật nhanh chóng và chính xác các lời giải bài tập Toán 9, đáp ứng nhu cầu học tập của học sinh trên toàn quốc.
Ông An có một bể kính hình lập phương như Hình 2. Ông An muốn làm thêm một bể kính mới hình lập phương có thể tích gấp n lần thể tích của bể kính cũ (bỏ qua bề dày của kính). a) Gọi a (dm) là độ dài cạnh của bể kính mới. Thay mỗi ? bằng biểu thức thích hợp để nhận được các đẳng thức: a3 = ? hay a = ?. b) Tính giá trị của a khi n = 8 và khi n = 4 (kết quả làm tròn đến chữ số thập phân thứ hai).
Video hướng dẫn giải
Trả lời câu hỏi Thực hành 4 trang 44 SGK Toán 9 Chân trời sáng tạo
Cho biểu thức Q = \(\sqrt[3]{{3{x^2}}}\). Tính giá trị của Q khi x = 2 và khi x = - 3 (kết quả làm tròn đến chữ số thập phân thứ hai).
Phương pháp giải:
Thay lần lượt giá trị của x vào biểu thức Q để tính.
Lời giải chi tiết:
Khi x = 2 suy ra Q = \(\sqrt[3]{{{{3.2}^2}}} \approx 2,29\).
Khi x = - 3 suy ra Q = \(\sqrt[3]{{3.{{( - 3)}^2}}} = 3\).
Video hướng dẫn giải
Trả lời câu hỏi Hoạt động 2 trang 44 SGK Toán 9 Chân trời sáng tạo
Ông An có một bể kính hình lập phương như Hình 2.
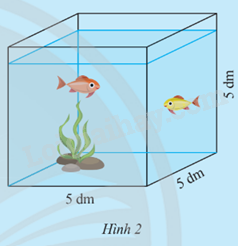
Ông An muốn làm thêm một bể kính mới hình lập phương có thể tích gấp n lần thể tích của bể kính cũ (bỏ qua bề dày của kính).
a) Gọi a (dm) là độ dài cạnh của bể kính mới. Thay mỗi ? bằng biểu thức thích hợp để nhận được các đẳng thức:
a3 = ? hay a = ?.
b) Tính giá trị của a khi n = 8 và khi n = 4 (kết quả làm tròn đến chữ số thập phân thứ hai).
Phương pháp giải:
- Sử dụng công thức thể tích lập phương V = cạnh.cạnh.cạnh
- Thay lần lượt giá trị n để tính.
Lời giải chi tiết:
a) a3 = (5.5.5).n = 125n hay a = \(\sqrt[3]{{125n}} = 5\sqrt[3]{n}\).
b) Khi n = 8, ta được: a = \(5\sqrt[3]{n} = 5\sqrt[3]{8} = 5.2 = 10\)
Khi n = 4, ta được: a = \(5\sqrt[3]{n} = 5\sqrt[3]{4} \approx 7,94\).
Video hướng dẫn giải
Trả lời câu hỏi Hoạt động 2 trang 44 SGK Toán 9 Chân trời sáng tạo
Ông An có một bể kính hình lập phương như Hình 2.
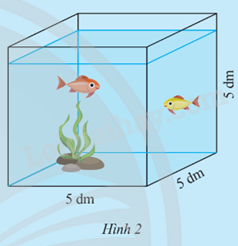
Ông An muốn làm thêm một bể kính mới hình lập phương có thể tích gấp n lần thể tích của bể kính cũ (bỏ qua bề dày của kính).
a) Gọi a (dm) là độ dài cạnh của bể kính mới. Thay mỗi ? bằng biểu thức thích hợp để nhận được các đẳng thức:
a3 = ? hay a = ?.
b) Tính giá trị của a khi n = 8 và khi n = 4 (kết quả làm tròn đến chữ số thập phân thứ hai).
Phương pháp giải:
- Sử dụng công thức thể tích lập phương V = cạnh.cạnh.cạnh
- Thay lần lượt giá trị n để tính.
Lời giải chi tiết:
a) a3 = (5.5.5).n = 125n hay a = \(\sqrt[3]{{125n}} = 5\sqrt[3]{n}\).
b) Khi n = 8, ta được: a = \(5\sqrt[3]{n} = 5\sqrt[3]{8} = 5.2 = 10\)
Khi n = 4, ta được: a = \(5\sqrt[3]{n} = 5\sqrt[3]{4} \approx 7,94\).
Video hướng dẫn giải
Trả lời câu hỏi Thực hành 4 trang 44 SGK Toán 9 Chân trời sáng tạo
Cho biểu thức Q = \(\sqrt[3]{{3{x^2}}}\). Tính giá trị của Q khi x = 2 và khi x = - 3 (kết quả làm tròn đến chữ số thập phân thứ hai).
Phương pháp giải:
Thay lần lượt giá trị của x vào biểu thức Q để tính.
Lời giải chi tiết:
Khi x = 2 suy ra Q = \(\sqrt[3]{{{{3.2}^2}}} \approx 2,29\).
Khi x = - 3 suy ra Q = \(\sqrt[3]{{3.{{( - 3)}^2}}} = 3\).
Mục 3 trang 44 SGK Toán 9 tập 1 - Chân trời sáng tạo thường xoay quanh các bài toán liên quan đến hàm số bậc nhất, đồ thị hàm số và ứng dụng của hàm số trong thực tế. Việc nắm vững kiến thức nền tảng về hàm số là vô cùng quan trọng để giải quyết các bài toán này một cách hiệu quả.
Mục 3 thường tập trung vào việc:
Để giải các bài toán trong Mục 3 trang 44 SGK Toán 9 tập 1 - Chân trời sáng tạo, học sinh cần:
Bài tập: Tìm giao điểm của hai đường thẳng y = 2x + 1 và y = -x + 4.
Giải:
Để tìm giao điểm của hai đường thẳng, ta giải hệ phương trình:
| y = 2x + 1 | y = -x + 4 |
Thay y = 2x + 1 vào phương trình y = -x + 4, ta được:
2x + 1 = -x + 4
3x = 3
x = 1
Thay x = 1 vào phương trình y = 2x + 1, ta được:
y = 2(1) + 1 = 3
Vậy giao điểm của hai đường thẳng là (1; 3).
Để học tốt môn Toán 9 và giải quyết các bài tập trong Mục 3 trang 44 SGK Toán 9 tập 1 - Chân trời sáng tạo, học sinh nên:
Giải mục 3 trang 44 SGK Toán 9 tập 1 - Chân trời sáng tạo đòi hỏi học sinh phải nắm vững kiến thức về hàm số và rèn luyện kỹ năng giải toán thường xuyên. Hy vọng với những hướng dẫn và ví dụ minh họa trên, các em học sinh sẽ tự tin hơn trong quá trình học tập và giải bài tập.