Bài học này cung cấp kiến thức nền tảng và chuyên sâu về đường tròn ngoại tiếp và nội tiếp tam giác trong chương trình Toán 9 Chân trời sáng tạo. Chúng ta sẽ cùng tìm hiểu định nghĩa, tính chất, cách xác định và ứng dụng của hai loại đường tròn này trong giải toán.
Nội dung bài học được trình bày một cách dễ hiểu, kèm theo các ví dụ minh họa và bài tập thực hành để giúp học sinh nắm vững kiến thức và rèn luyện kỹ năng giải toán.
1. Đường tròn ngoại tiếp tam giác Định nghĩa đường tròn ngoại tiếp tam giác
1. Đường tròn ngoại tiếp tam giác
Định nghĩa đường tròn ngoại tiếp tam giác
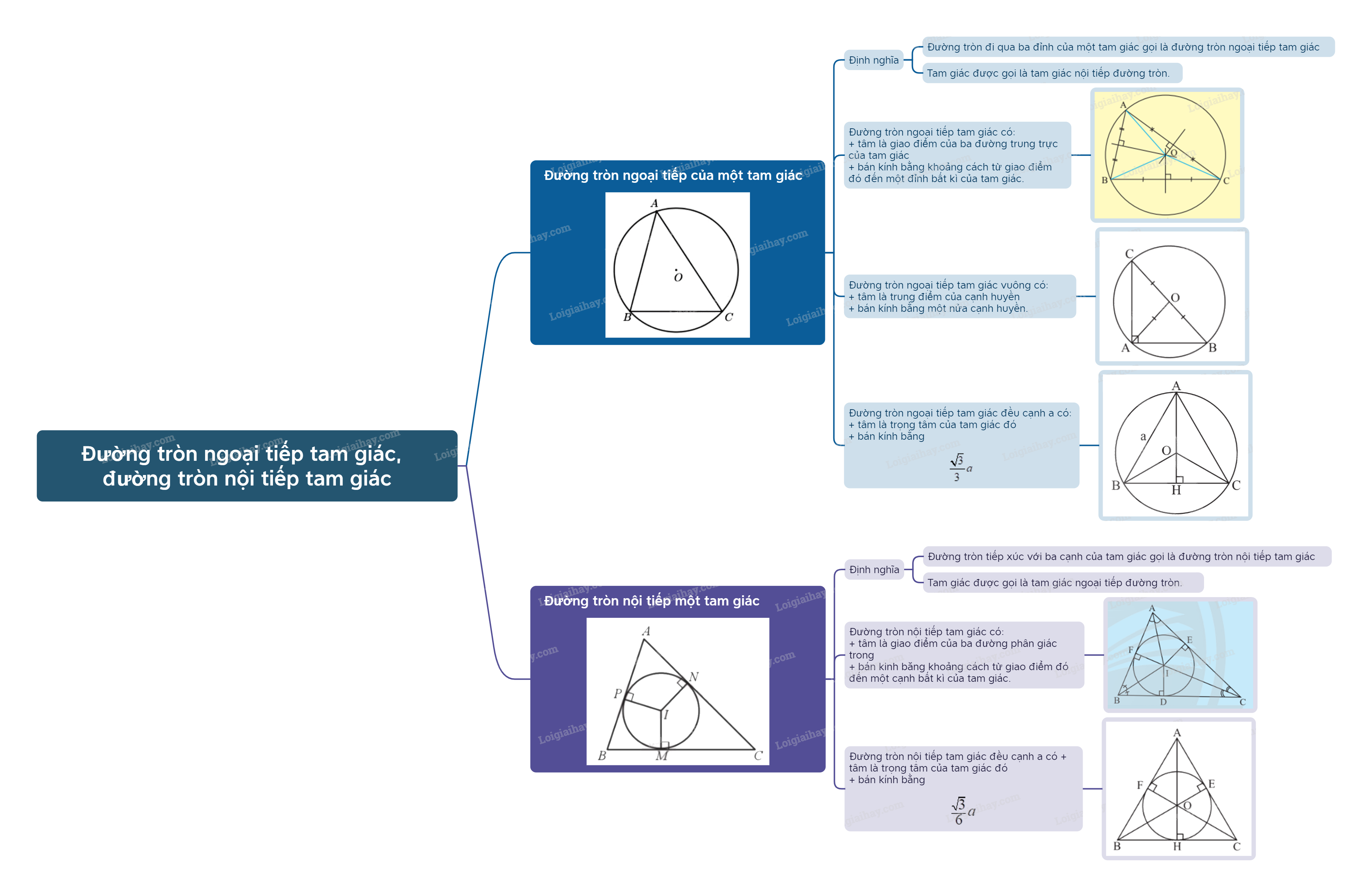
– Đường tròn đi qua ba đỉnh của một tam giác gọi là đường tròn ngoại tiếp tam giác, khi đó tam giác được gọi là tam giác nội tiếp đường tròn. – Đường tròn ngoại tiếp tam giác có tâm là giao điểm của ba đường trung trực của tam giác và có bán kính bằng khoảng cách từ giao điểm đó đến một đỉnh bất kì của tam giác.
|
Ví dụ:
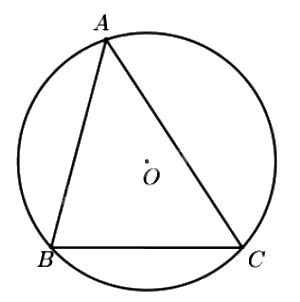
- Đường tròn (O) ngoại tiếp tam giác ABC. Tam giác ABC nội tiếp đường tròn (O).
- Tâm O là giao điểm của ba đường trung trực của tam giác ABC.
Đường tròn ngoại tiếp tam giác đều
Đường tròn ngoại tiếp tam giác đều cạnh a có tâm là trọng tâm của tam giác đó và bán kính bằng \(\frac{{\sqrt 3 }}{3}a\).
|
Ví dụ:
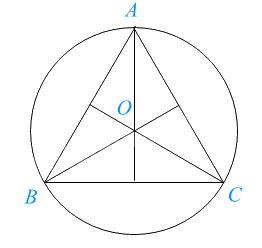
Đường tròn (O) ngoại tiếp tam giác đều ABC, bán kính \(OA = OB = OC = \frac{{\sqrt 3 }}{3}AB\).
Đường tròn ngoại tiếp tam giác vuông
Đường tròn ngoại tiếp tam giác vuông có tâm là trung điểm của cạnh huyền và bán kính bằng một nửa cạnh huyền.
|
Ví dụ:
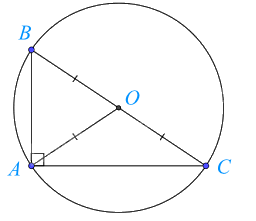
Tam giác ABC nội tiếp đường tròn (O; BO).
2. Đường tròn nội tiếp một tam giác
Định nghĩa đường tròn nội tiếp tam giác
- Đường tròn tiếp xúc với ba cạnh của tam giác gọi là đường tròn nội tiếp tam giác, khi đó tam giác được gọi là tam giác ngoại tiếpđường tròn. - Đường tròn nội tiếp tam giác có tâm là giao điểm của ba đường phân giác trong và bán kinh bằng khoảng cách từ giao điểm đó đến một cạnh bất kì của tam giác.
|
Ví dụ:
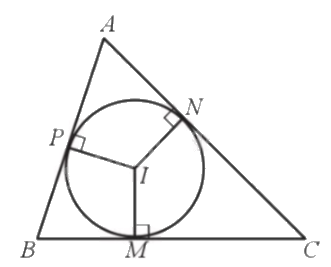
- Đường tròn (I) nội tiếp tam giác ABC. Tam giác ABC ngoại tiếp đường tròn (I).
- Tâm I là giao điểm của ba đường phân giác của tam giác.
Đường tròn nội tiếp tam giác đều
Đường tròn nội tiếp tam giác đều cạnh a có tâm là trọng tâm của tam giác đó và bán kính bằng \(\frac{{\sqrt 3 }}{6}a\).
|
Ví dụ:
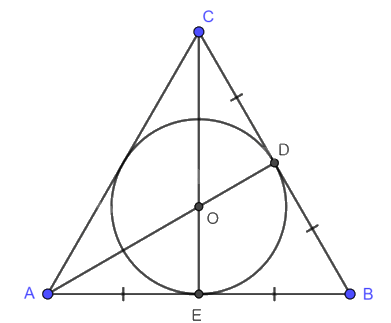
Đường tròn (O) nội tiếp tam giác đều ABC, bán kính \(OD = OE = \frac{{\sqrt 3 }}{6}AB\).
Trong hình học, đường tròn đóng vai trò quan trọng trong việc nghiên cứu các tính chất và mối quan hệ giữa các điểm và đường thẳng. Đặc biệt, đường tròn ngoại tiếp và nội tiếp tam giác là những khái niệm cơ bản và thường xuyên xuất hiện trong các bài toán hình học.
Định nghĩa: Đường tròn ngoại tiếp tam giác là đường tròn đi qua ba đỉnh của tam giác đó.
Tâm đường tròn ngoại tiếp: Giao điểm của các đường trung trực của tam giác.
Bán kính đường tròn ngoại tiếp: Khoảng cách từ tâm đường tròn ngoại tiếp đến một đỉnh của tam giác. Ký hiệu là R.
Công thức tính bán kính R:
Tính chất:
Định nghĩa: Đường tròn nội tiếp tam giác là đường tròn tiếp xúc với cả ba cạnh của tam giác đó.
Tâm đường tròn nội tiếp: Giao điểm của các đường phân giác của tam giác.
Bán kính đường tròn nội tiếp: Khoảng cách từ tâm đường tròn nội tiếp đến một cạnh của tam giác. Ký hiệu là r.
Công thức tính bán kính r:
Tính chất:
Công thức Euler: d2 = R(R - 2r), trong đó d là khoảng cách giữa tâm đường tròn ngoại tiếp và tâm đường tròn nội tiếp.
Đường tròn ngoại tiếp và nội tiếp thường được sử dụng để giải các bài toán liên quan đến tính góc, tính độ dài cạnh, chứng minh các mối quan hệ hình học trong tam giác.
Bài 1: Cho tam giác ABC vuông tại A, AB = 3cm, AC = 4cm. Tính bán kính đường tròn ngoại tiếp và nội tiếp của tam giác ABC.
Giải:
Bài 2:...
Việc nắm vững lý thuyết về đường tròn ngoại tiếp và nội tiếp tam giác là rất quan trọng để giải quyết các bài toán hình học trong chương trình Toán 9 Chân trời sáng tạo. Hy vọng bài học này đã cung cấp cho bạn những kiến thức hữu ích và giúp bạn tự tin hơn trong việc học tập.