Chào mừng các em học sinh đến với chuyên mục giải bài tập Toán 9 tập 1 của giaitoan.edu.vn. Ở bài viết này, chúng tôi sẽ cung cấp lời giải chi tiết và dễ hiểu cho các bài tập trong mục 1 trang 67, 68 sách giáo khoa Toán 9 tập 1 - Chân trời sáng tạo.
Mục tiêu của chúng tôi là giúp các em nắm vững kiến thức, rèn luyện kỹ năng giải toán và đạt kết quả tốt nhất trong học tập.
Cho tam giác ABC vuông tại A (Hình 1). a) Hãy tính sin B theo b và a, cos B theo c và a. Sử dụng các kết quả tính được để giải thích tại sao ta lại có các đẳng thức: b = a.sin B c = a.cos B b) Hãy tính tan B theo b và c, cot B theo c và b. Sử dụng các kết quả tính được ở trên để giải thích tại sao ta lại có các đẳng thức: b = c.tan B c = b.cot B.
Video hướng dẫn giải
Trả lời câu hỏi Hoạt động 1 trang 67 SGK Toán 9 Chân trời sáng tạo
Cho tam giác ABC vuông tại A (Hình 1).
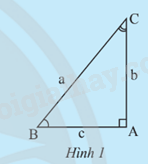
a) Hãy tính sin B theo b và a, cos B theo c và a. Sử dụng các kết quả tính được để giải thích tại sao ta lại có các đẳng thức:
b = a.sin B
c = a.cos B
b) Hãy tính tan B theo b và c, cot B theo c và b. Sử dụng các kết quả tính được ở trên để giải thích tại sao ta lại có các đẳng thức:
b = c.tan B
c = b.cot B.
Phương pháp giải:
Dựa vào tỉ số lượng giác của góc nhọn. Xét tam giác vuông ABC:
+ Tỉ số giữa cạnh đối và cạnh huyền được gọi là sin, kí hiệu sin.
+ Tỉ số giữa cạnh kề và cạnh huyền được gọi là côsin, kí hiệu cos.
+ Tỉ số giữa cạnh đối và cạnh kề được gọi là tang, kí hiệu tan.
+ Tỉ số giữa cạnh kề và cạnh đối được gọi là côtang , kí hiệu cot.
Lời giải chi tiết:
Xét tam giác vuông ABC, ta có:
a) \(\sin B = \frac{{AC}}{{BC}} = \frac{b}{a}\) suy ra b = a.sin B
\(\cos B = \frac{{AB}}{{BC}} = \frac{c}{a}\) suy ra c = a.cos B
b) \(\tan B = \frac{{AC}}{{AB}} = \frac{b}{c}\) suy ra b = c.tan B
\(\cot B = \frac{{AB}}{{AC}} = \frac{c}{b}\) suy ra c = b.cot B.
Video hướng dẫn giải
Trả lời câu hỏi Thực hành 1 trang 68SGK Toán 9 Chân trời sáng tạo
Cho tam giác ABC vuông tại A có độ dài cạnh huyền bằng 20cm. Tính độ dài các cạnh góc vuông trong mỗi trường hợp sau (kết quả làm tròn đến hàng phần trăm)
a) \(\widehat B = {36^o}\)
b) \(\widehat C = {41^o}\)
Phương pháp giải:
- Đọc kĩ dữ liệu đề bài để vẽ hình
- Dựa vào định lí: Xét tam giác vuông:
+ Mỗi cạnh góc vuông bằng cạnh huyền nhân sin góc đối hoặc nhân côsin góc kề rồi suy ra cạnh góc vuông và áp dụng định lý Pythagore tính cạnh góc vuông còn lại.
+ Mỗi cạnh góc vuông bằng cạnh góc vuông còn lại nhân tang góc đối hoặc nhân côtang góc kề rồi suy ra cạnh góc vuông và áp dụng định lý Pythagore tính cạnh góc vuông còn lại.
Lời giải chi tiết:
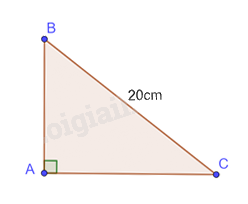
a) Với \(\widehat B = {36^o}\), cạnh góc vuông AB có góc kề bằng \({36^o}\) nên ta có:
AB = cos\({36^o}.BC \approx 16,18cm\)
Áp dụng định lí Pythagore vào tam giác ABC vuông tại A ta có:
\(AC = \sqrt {B{C^2} - A{B^2}} \approx \sqrt {{{20}^2} - 16,{{18}^2}} \approx 11,76cm\)
b) Với \(\widehat C = {41^o}\), cạnh góc vuông AB có góc đối bằng \({41^o}\) nên ta có:
AB = sin\(\widehat C.BC \approx 13,12cm\)
Áp dụng định lí Pythagore vào tam giác ABC vuông tại A ta có:
\(AC = \sqrt {B{C^2} - A{B^2}} \approx \sqrt {{{20}^2} - 13,{{12}^2}} \approx 15,1cm\)
Video hướng dẫn giải
Trả lời câu hỏi Vận dụng 1 trang 68 SGK Toán 9 Chân trời sáng tạo
Một cần cẩu đang nâng một khối gỗ trên sông. Biết tay cần cẩu AB có chiều dài là 16m và nghiêng một góc \({42^o}\) so với phương nằm ngang (Hình 4). Tính chiều dài BC của đoạn dây cáp (kết quả làm tròn đến hàng phần mười).
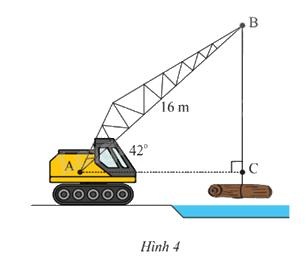
Phương pháp giải:
Dựa vào định lí: Xét tam giác vuông, mỗi cạnh góc vuông bằng cạnh huyền nhân sin góc đối hoặc nhân côsin góc kề rồi suy ra cạnh góc vuông.
Lời giải chi tiết:
Xét tam giác ABC vuông tại C, \(\widehat A = {42^o}\), ta có:
\(BC = \sin {42^o}.AB = \sin {42^o}.16 \approx 10,7 m\)
Video hướng dẫn giải
Trả lời câu hỏi Thực hành 2 trang 68SGK Toán 9 Chân trời sáng tạo
Tính độ dài cạnh góc vuông x của mỗi tam giác vuông trong Hình 3 (kết quả làm tròn đến hàng phần trăm).
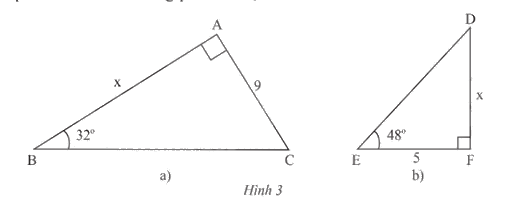
Phương pháp giải:
Dựa vào định lí: Xét tam giác vuông:
+ Mỗi cạnh góc vuông bằng cạnh huyền nhân sin góc đối hoặc nhân côsin góc kề rồi suy ra cạnh góc vuông.
+ Mỗi cạnh góc vuông bằng cạnh góc vuông còn lại nhân tang góc đối hoặc nhân côtang góc kề rồi suy ra cạnh góc vuông.
Lời giải chi tiết:
a) Xét tam giác ABC vuông tại A. \(\widehat B = {32^o}\), ta có:
x = AB = AC. cot \({32^o}\) = 9. cot\({32^o}\)\( \approx \) 14,4
b) Xét tam giác DEF vuông tại F. \(\widehat E = {48^o}\), ta có:
x = DF = EF. tan \({48^o}\) = 5. tan \({48^o}\)\( \approx \) 5,55
Video hướng dẫn giải
Trả lời câu hỏi Hoạt động 1 trang 67 SGK Toán 9 Chân trời sáng tạo
Cho tam giác ABC vuông tại A (Hình 1).
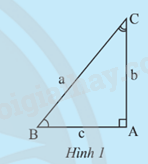
a) Hãy tính sin B theo b và a, cos B theo c và a. Sử dụng các kết quả tính được để giải thích tại sao ta lại có các đẳng thức:
b = a.sin B
c = a.cos B
b) Hãy tính tan B theo b và c, cot B theo c và b. Sử dụng các kết quả tính được ở trên để giải thích tại sao ta lại có các đẳng thức:
b = c.tan B
c = b.cot B.
Phương pháp giải:
Dựa vào tỉ số lượng giác của góc nhọn. Xét tam giác vuông ABC:
+ Tỉ số giữa cạnh đối và cạnh huyền được gọi là sin, kí hiệu sin.
+ Tỉ số giữa cạnh kề và cạnh huyền được gọi là côsin, kí hiệu cos.
+ Tỉ số giữa cạnh đối và cạnh kề được gọi là tang, kí hiệu tan.
+ Tỉ số giữa cạnh kề và cạnh đối được gọi là côtang , kí hiệu cot.
Lời giải chi tiết:
Xét tam giác vuông ABC, ta có:
a) \(\sin B = \frac{{AC}}{{BC}} = \frac{b}{a}\) suy ra b = a.sin B
\(\cos B = \frac{{AB}}{{BC}} = \frac{c}{a}\) suy ra c = a.cos B
b) \(\tan B = \frac{{AC}}{{AB}} = \frac{b}{c}\) suy ra b = c.tan B
\(\cot B = \frac{{AB}}{{AC}} = \frac{c}{b}\) suy ra c = b.cot B.
Video hướng dẫn giải
Trả lời câu hỏi Thực hành 1 trang 68SGK Toán 9 Chân trời sáng tạo
Cho tam giác ABC vuông tại A có độ dài cạnh huyền bằng 20cm. Tính độ dài các cạnh góc vuông trong mỗi trường hợp sau (kết quả làm tròn đến hàng phần trăm)
a) \(\widehat B = {36^o}\)
b) \(\widehat C = {41^o}\)
Phương pháp giải:
- Đọc kĩ dữ liệu đề bài để vẽ hình
- Dựa vào định lí: Xét tam giác vuông:
+ Mỗi cạnh góc vuông bằng cạnh huyền nhân sin góc đối hoặc nhân côsin góc kề rồi suy ra cạnh góc vuông và áp dụng định lý Pythagore tính cạnh góc vuông còn lại.
+ Mỗi cạnh góc vuông bằng cạnh góc vuông còn lại nhân tang góc đối hoặc nhân côtang góc kề rồi suy ra cạnh góc vuông và áp dụng định lý Pythagore tính cạnh góc vuông còn lại.
Lời giải chi tiết:
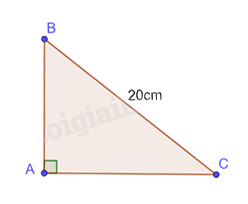
a) Với \(\widehat B = {36^o}\), cạnh góc vuông AB có góc kề bằng \({36^o}\) nên ta có:
AB = cos\({36^o}.BC \approx 16,18cm\)
Áp dụng định lí Pythagore vào tam giác ABC vuông tại A ta có:
\(AC = \sqrt {B{C^2} - A{B^2}} \approx \sqrt {{{20}^2} - 16,{{18}^2}} \approx 11,76cm\)
b) Với \(\widehat C = {41^o}\), cạnh góc vuông AB có góc đối bằng \({41^o}\) nên ta có:
AB = sin\(\widehat C.BC \approx 13,12cm\)
Áp dụng định lí Pythagore vào tam giác ABC vuông tại A ta có:
\(AC = \sqrt {B{C^2} - A{B^2}} \approx \sqrt {{{20}^2} - 13,{{12}^2}} \approx 15,1cm\)
Video hướng dẫn giải
Trả lời câu hỏi Thực hành 2 trang 68SGK Toán 9 Chân trời sáng tạo
Tính độ dài cạnh góc vuông x của mỗi tam giác vuông trong Hình 3 (kết quả làm tròn đến hàng phần trăm).

Phương pháp giải:
Dựa vào định lí: Xét tam giác vuông:
+ Mỗi cạnh góc vuông bằng cạnh huyền nhân sin góc đối hoặc nhân côsin góc kề rồi suy ra cạnh góc vuông.
+ Mỗi cạnh góc vuông bằng cạnh góc vuông còn lại nhân tang góc đối hoặc nhân côtang góc kề rồi suy ra cạnh góc vuông.
Lời giải chi tiết:
a) Xét tam giác ABC vuông tại A. \(\widehat B = {32^o}\), ta có:
x = AB = AC. cot \({32^o}\) = 9. cot\({32^o}\)\( \approx \) 14,4
b) Xét tam giác DEF vuông tại F. \(\widehat E = {48^o}\), ta có:
x = DF = EF. tan \({48^o}\) = 5. tan \({48^o}\)\( \approx \) 5,55
Video hướng dẫn giải
Trả lời câu hỏi Vận dụng 1 trang 68 SGK Toán 9 Chân trời sáng tạo
Một cần cẩu đang nâng một khối gỗ trên sông. Biết tay cần cẩu AB có chiều dài là 16m và nghiêng một góc \({42^o}\) so với phương nằm ngang (Hình 4). Tính chiều dài BC của đoạn dây cáp (kết quả làm tròn đến hàng phần mười).
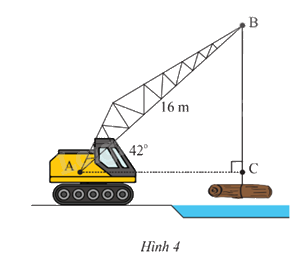
Phương pháp giải:
Dựa vào định lí: Xét tam giác vuông, mỗi cạnh góc vuông bằng cạnh huyền nhân sin góc đối hoặc nhân côsin góc kề rồi suy ra cạnh góc vuông.
Lời giải chi tiết:
Xét tam giác ABC vuông tại C, \(\widehat A = {42^o}\), ta có:
\(BC = \sin {42^o}.AB = \sin {42^o}.16 \approx 10,7 m\)
Mục 1 của chương trình Toán 9 tập 1 - Chân trời sáng tạo tập trung vào việc ôn tập và hệ thống hóa kiến thức về hàm số bậc nhất. Các bài tập trong trang 67 và 68 SGK Toán 9 tập 1 yêu cầu học sinh vận dụng các kiến thức đã học để giải quyết các bài toán thực tế, rèn luyện tư duy logic và kỹ năng giải toán.
Bài tập này yêu cầu học sinh xác định các hệ số a, b trong hàm số bậc nhất y = ax + b dựa vào các thông tin cho trước, chẳng hạn như đồ thị hàm số, các điểm thuộc đồ thị hàm số hoặc các điều kiện khác.
Ví dụ:
Bài tập này yêu cầu học sinh vẽ đồ thị hàm số bậc nhất dựa vào các thông tin đã cho. Để vẽ đồ thị hàm số, học sinh cần xác định ít nhất hai điểm thuộc đồ thị hàm số, sau đó nối hai điểm này lại với nhau bằng một đường thẳng.
Ví dụ:
Bài tập này yêu cầu học sinh tìm tọa độ giao điểm của hai đường thẳng. Để tìm giao điểm của hai đường thẳng, học sinh cần giải hệ phương trình bậc nhất hai ẩn tương ứng với hai đường thẳng đó.
Ví dụ:
Bài tập này yêu cầu học sinh vận dụng kiến thức về hàm số bậc nhất để giải quyết các bài toán thực tế, chẳng hạn như bài toán về quãng đường, thời gian, tốc độ, hoặc bài toán về lợi nhuận, chi phí.
Ví dụ:
| Công thức | Mô tả |
|---|---|
| y = ax + b | Hàm số bậc nhất |
| a | Hệ số góc |
| b | Giao điểm với trục Oy |
Hy vọng với lời giải chi tiết và những hướng dẫn trên, các em học sinh sẽ tự tin hơn khi giải các bài tập trong mục 1 trang 67, 68 SGK Toán 9 tập 1 - Chân trời sáng tạo. Chúc các em học tập tốt!