Bài học này cung cấp lý thuyết đầy đủ và chi tiết về cách biến đổi đơn giản biểu thức chứa căn thức bậc hai, thuộc chương trình Toán 9 Chân trời sáng tạo.
Chúng ta sẽ cùng nhau tìm hiểu các quy tắc, tính chất quan trọng và các ví dụ minh họa để nắm vững kiến thức này.
Đây là nền tảng vững chắc để giải các bài tập liên quan đến căn thức bậc hai một cách hiệu quả.
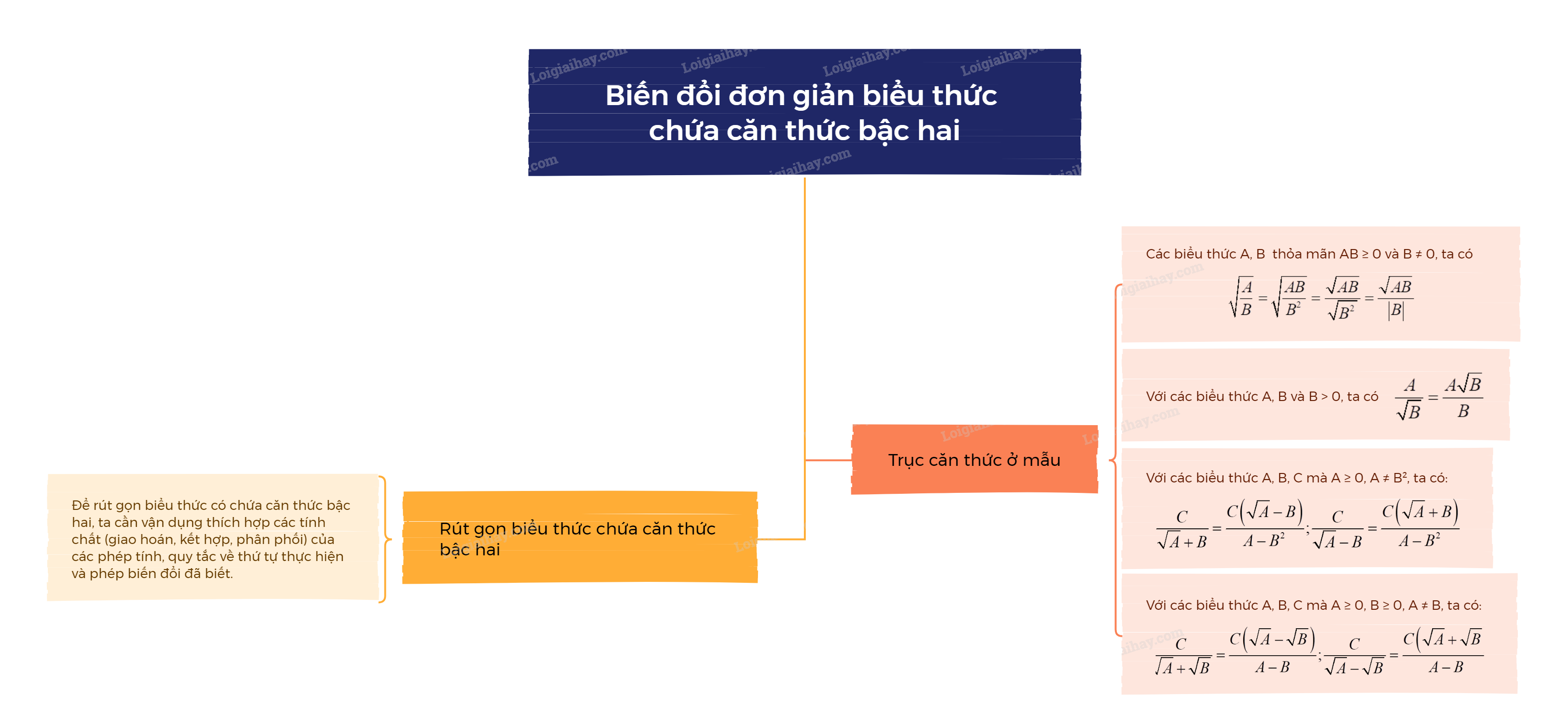
1. Trục căn thức ở mẫu - Với các biểu thức A và B thỏa mãn \(AB \ge 0,B \ne 0\), ta có: \(\sqrt {\frac{A}{B}} = \sqrt {\frac{{AB}}{{{B^2}}}} = \frac{{\sqrt {AB} }}{{\sqrt {{B^2}} }} = \frac{{\sqrt {AB} }}{{\left| B \right|}}\). - Với các biểu thức A, B và B > 0, ta có \(\frac{A}{{\sqrt B }} = \frac{{A\sqrt B }}{B}\). - Với các biểu thức A, B, C mà \(A \ge 0,A \ne {B^2}\), ta có: \(\frac{C}{{\sqrt A + B}} = \frac{{C\left( {\sqrt A - B} \right)}}{{A - {B^2}}};\frac{C}{{\sqrt A - B}} = \f
1. Trục căn thức ở mẫu
- Với các biểu thức A và B thỏa mãn \(AB \ge 0,B \ne 0\), ta có: \(\sqrt {\frac{A}{B}} = \sqrt {\frac{{AB}}{{{B^2}}}} = \frac{{\sqrt {AB} }}{{\sqrt {{B^2}} }} = \frac{{\sqrt {AB} }}{{\left| B \right|}}\). - Với các biểu thức A, B và B > 0, ta có \(\frac{A}{{\sqrt B }} = \frac{{A\sqrt B }}{B}\). - Với các biểu thức A, B, C mà \(A \ge 0,A \ne {B^2}\), ta có: \(\frac{C}{{\sqrt A + B}} = \frac{{C\left( {\sqrt A - B} \right)}}{{A - {B^2}}};\frac{C}{{\sqrt A - B}} = \frac{{C\left( {\sqrt A + B} \right)}}{{A - {B^2}}}\). - Với các biểu thức A, B, C mà \(A \ge 0,B \ge 0,A \ne B\), ta có: \(\frac{C}{{\sqrt A + \sqrt B }} = \frac{{C\left( {\sqrt A - \sqrt B } \right)}}{{A - B}};\frac{C}{{\sqrt A - \sqrt B }} = \frac{{C\left( {\sqrt A + \sqrt B } \right)}}{{A - B}}\). |
Ví dụ:
\(\frac{2}{{3\sqrt 5 }} = \frac{{2\sqrt 5 }}{{3{{\left( {\sqrt 5 } \right)}^2}}} = \frac{{2\sqrt 5 }}{{3.5}} = \frac{{2\sqrt 5 }}{{15}}\);
\(\frac{a}{{3 - 2\sqrt 2 }} = \frac{{a\left( {3 + 2\sqrt 2 } \right)}}{{\left( {3 - 2\sqrt 2 } \right).\left( {3 + 2\sqrt 2 } \right)}} = \frac{{a\left( {3 + 2\sqrt 2 } \right)}}{{{3^2} - {{\left( {2\sqrt 2 } \right)}^2}}} = \frac{{a\left( {3 + 2\sqrt 2 } \right)}}{{9 - 8}} = \left( {3 + 2\sqrt 2 } \right)a\).
2. Rút gọn biểu thức chứa căn thức bậc hai
Để rút gọn biểu thức có chứa căn thức bậc hai, ta cần vận dụng thích hợp các tính chất (giao hoán, kết hợp, phân phối) của các phép tính, quy tắc về thứ tự thực hiện và phép biến đổi đã biết. |
Ví dụ:
\(\begin{array}{l}A = 2\sqrt 3 - \sqrt {75} + \sqrt {{{\left( {1 - \sqrt 3 } \right)}^2}} \\ = 2\sqrt 3 - \sqrt {{{3.5}^2}} + \left| {1 - \sqrt 3 } \right|\\ = 2\sqrt 3 - 5\sqrt 3 + \sqrt 3 - 1\\ = - 1 - 2\sqrt 3 \end{array}\)
\(\begin{array}{l}B = x\sqrt x - \frac{{{x^2} - x}}{{\sqrt x + 1}}\\ = x\sqrt x - \frac{{\left( {{x^2} - x} \right)\left( {\sqrt x - 1} \right)}}{{\left( {\sqrt x + 1} \right)\left( {\sqrt x - 1} \right)}}\\ = x\sqrt x - \frac{{x\left( {x - 1} \right)\left( {\sqrt x - 1} \right)}}{{\left( {\sqrt x + 1} \right)\left( {\sqrt x - 1} \right)}}\\ = x\sqrt x - \frac{{x\left( {x - 1} \right)\left( {\sqrt x - 1} \right)}}{{x - 1}}\\ = x\sqrt x - x\left( {\sqrt x - 1} \right)\\ = x\sqrt x - x\sqrt x + x\\ = x\end{array}\)
Trong chương trình Toán 9, việc nắm vững kiến thức về căn thức bậc hai và các phép biến đổi liên quan là vô cùng quan trọng. Bài viết này sẽ trình bày chi tiết lý thuyết về biến đổi đơn giản biểu thức chứa căn thức bậc hai, theo chương trình Chân trời sáng tạo.
Căn thức bậc hai của một số thực a (với a ≥ 0) là số x sao cho x2 = a. Ký hiệu: √a. Ví dụ: √9 = 3, √16 = 4.
Ví dụ 1: Đưa thừa số ra ngoài dấu căn: √(27) = √(9.3) = √9 . √3 = 3√3
Ví dụ 2: Đưa thừa số vào trong dấu căn: 2√5 = √(22.5) = √20
Ví dụ 3: Khai phương một tích: √(4.9) = √4 . √9 = 2 . 3 = 6
Ví dụ 4: Khai phương một thương: √(16/25) = √16 / √25 = 4/5
Hãy áp dụng các quy tắc trên để biến đổi các biểu thức sau:
Trong nhiều bài toán, biểu thức chứa căn thức có thể phức tạp hơn. Để biến đổi, ta cần kết hợp các quy tắc đã học và sử dụng các kỹ năng đại số khác như phân tích đa thức thành nhân tử, sử dụng hằng đẳng thức, v.v.
Việc biến đổi đơn giản biểu thức chứa căn thức bậc hai có nhiều ứng dụng trong toán học và thực tế, bao gồm:
Lý thuyết về biến đổi đơn giản biểu thức chứa căn thức bậc hai là một phần quan trọng của chương trình Toán 9 Chân trời sáng tạo. Việc nắm vững các quy tắc và áp dụng chúng một cách linh hoạt sẽ giúp học sinh giải quyết các bài toán một cách hiệu quả và chính xác.
| Quy tắc | Ví dụ |
|---|---|
| Đưa thừa số ra ngoài dấu căn | √(18) = 3√2 |
| Đưa thừa số vào trong dấu căn | 4√3 = √48 |
| Khai phương một tích | √(25.36) = 5.6 = 30 |