Chào mừng các em học sinh đến với bài giải chi tiết mục 3 trang 86, 87 SGK Toán 9 tập 2 - Chân trời sáng tạo trên giaitoan.edu.vn. Bài viết này sẽ cung cấp lời giải đầy đủ, dễ hiểu cho từng bài tập, giúp các em nắm vững kiến thức và tự tin hơn trong quá trình học tập.
Chúng tôi luôn cố gắng mang đến những giải pháp học tập hiệu quả nhất, hỗ trợ các em học sinh chinh phục môn Toán một cách dễ dàng.
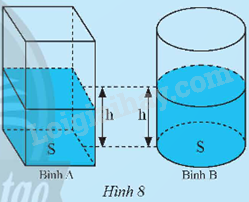
Cho hai cái bình có cùng diện tích đáy: bình A có dạng hình hộp chữ nhật, hình B có dạng hình trụ. Ban đầu cả hai bình đều không chứa nước. Người ta đổ cùng một lượng nước vào hai bình thì thấy chiều cao của mực nước hai bình bằng nhau (Hình 8). Gọi S là diện tích đáy và h là chiều cao của mực nước mỗi bình. a) Tính thể tích V của lượng nước trong bình A theo S và h. Từ đó, dự đoán thể tích của lượng nước trong bình B. b) Gọi r là bán kính đáy hình B. Hãy tính thể tích nước trong bình B theo r
Trả lời câu hỏi Thực hành 3 trang 87 SGK Toán 9 Chân trời sáng tạo
Phần bên trong của một cái bể hình trụ có chiều cao 2,1 m và bán kính đáy 1,5 m. Tính thể tích lượng nước trong bể biết mực nước bằng \(\frac{2}{3}\)chiều cao của bể (kết quả làm tròn đến hàng đơn vị).
Phương pháp giải:
Dựa vào công thức tính thể tích của hình trụ: V = S.h = \(\pi \)r2h
Lời giải chi tiết:
Thể tích của bể là: V = \(\pi \)r2h = \(\pi \).1,52.2,1 = 4,725\(\pi \) (m3).
Thể tích lượng nước trong bể là:
\(V' = \frac{2}{3}V = \frac{2}{3}.4,725\pi \approx\) 10 (m3).
Video hướng dẫn giải
Trả lời câu hỏi Hoạt động 3 trang 86 SGK Toán 9 Chân trời sáng tạo
Cho hai cái bình có cùng diện tích đáy: bình A có dạng hình hộp chữ nhật, hình B có dạng hình trụ. Ban đầu cả hai bình đều không chứa nước. Người ta đổ cùng một lượng nước vào hai bình thì thấy chiều cao của mực nước hai bình bằng nhau (Hình 8). Gọi S là diện tích đáy và h là chiều cao của mực nước mỗi bình.
a) Tính thể tích V của lượng nước trong bình A theo S và h. Từ đó, dự đoán thể tích của lượng nước trong bình B.
b) Gọi r là bán kính đáy hình B. Hãy tính thể tích nước trong bình B theo r và h.
Phương pháp giải:
Dựa vào dữ kiện đề bài rồi biến đổi theo S, h và r.
Lời giải chi tiết:
a) Thể tích V của lượng nước trong bình A là: V = S.h
Thể tích V của lượng nước trong bình B là: V = S.h
b) Thể tích V của lượng nước trong bình B là: V = S.h = \(\pi \)r2h.
Trả lời câu hỏi Thực hành 3 trang 87 SGK Toán 9 Chân trời sáng tạo
Phần bên trong của một cái bể hình trụ có chiều cao 2,1 m và bán kính đáy 1,5 m. Tính thể tích lượng nước trong bể biết mực nước bằng \(\frac{2}{3}\)chiều cao của bể (kết quả làm tròn đến hàng đơn vị).
Phương pháp giải:
Dựa vào công thức tính thể tích của hình trụ: V = S.h = \(\pi \)r2h
Lời giải chi tiết:
Thể tích của bể là: V = \(\pi \)r2h = \(\pi \).1,52.2,1 = 4,725\(\pi \) (m3).
Thể tích lượng nước trong bể là:
\(V' = \frac{2}{3}V = \frac{2}{3}.4,725\pi \approx\) 10 (m3).
Video hướng dẫn giải
Trả lời câu hỏi Hoạt động 3 trang 86 SGK Toán 9 Chân trời sáng tạo
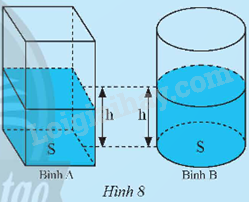
Cho hai cái bình có cùng diện tích đáy: bình A có dạng hình hộp chữ nhật, hình B có dạng hình trụ. Ban đầu cả hai bình đều không chứa nước. Người ta đổ cùng một lượng nước vào hai bình thì thấy chiều cao của mực nước hai bình bằng nhau (Hình 8). Gọi S là diện tích đáy và h là chiều cao của mực nước mỗi bình.
a) Tính thể tích V của lượng nước trong bình A theo S và h. Từ đó, dự đoán thể tích của lượng nước trong bình B.
b) Gọi r là bán kính đáy hình B. Hãy tính thể tích nước trong bình B theo r và h.
Phương pháp giải:
Dựa vào dữ kiện đề bài rồi biến đổi theo S, h và r.
Lời giải chi tiết:
a) Thể tích V của lượng nước trong bình A là: V = S.h
Thể tích V của lượng nước trong bình B là: V = S.h
b) Thể tích V của lượng nước trong bình B là: V = S.h = \(\pi \)r2h.
Mục 3 trong SGK Toán 9 tập 2 - Chân trời sáng tạo tập trung vào việc ôn tập chương về hàm số bậc hai. Các bài tập trong mục này thường yêu cầu học sinh vận dụng các kiến thức đã học để giải quyết các bài toán thực tế, rèn luyện kỹ năng tư duy logic và khả năng giải quyết vấn đề.
Bài 1 thường yêu cầu học sinh xác định các yếu tố của hàm số bậc hai (a, b, c), tìm đỉnh của parabol, trục đối xứng, và vẽ đồ thị hàm số. Để giải bài này, học sinh cần nắm vững các công thức và phương pháp đã học trong chương.
Bài 2 thường đưa ra các bài toán thực tế liên quan đến hàm số bậc hai, ví dụ như tìm chiều dài, chiều rộng của một hình chữ nhật để diện tích đạt giá trị lớn nhất. Để giải bài này, học sinh cần xây dựng được hàm số biểu diễn đại lượng cần tìm, sau đó tìm giá trị lớn nhất hoặc nhỏ nhất của hàm số đó.
Ví dụ: Một khu vườn hình chữ nhật có chu vi là 100m. Tìm chiều dài và chiều rộng của khu vườn để diện tích đạt giá trị lớn nhất.
Bài 3 yêu cầu học sinh giải các phương trình bậc hai bằng các phương pháp đã học (phân tích thành nhân tử, sử dụng công thức nghiệm, phương pháp hoàn thiện bình phương).
Ví dụ: Giải phương trình 2x2 - 5x + 2 = 0.
Ta có thể giải phương trình này bằng công thức nghiệm:
x = (-b ± √(b2 - 4ac)) / 2a = (5 ± √((-5)2 - 4 * 2 * 2)) / (2 * 2) = (5 ± √9) / 4
Vậy, phương trình có hai nghiệm: x1 = 2 và x2 = 1/2.
Hy vọng với bài giải chi tiết mục 3 trang 86, 87 SGK Toán 9 tập 2 - Chân trời sáng tạo này, các em học sinh sẽ tự tin hơn trong quá trình học tập và đạt kết quả tốt nhất. Chúc các em học tốt!