Chào mừng bạn đến với bài học về Lý thuyết Đa giác đều và phép quay trong chương trình Toán 9 Chân trời sáng tạo. Bài học này sẽ cung cấp cho bạn những kiến thức cơ bản và quan trọng nhất về các khái niệm này.
Chúng ta sẽ cùng nhau tìm hiểu định nghĩa, tính chất của đa giác đều, cách xác định tâm đối xứng, trục đối xứng của đa giác đều. Đồng thời, bài học cũng sẽ đi sâu vào phép quay, các tính chất của phép quay và ứng dụng của nó trong giải toán.
1. Khái niệm đa giác đều Đa giác - Đa giác ABCDE là hình gồm các đoạn thẳng AB, BC, CD, DE và EA, trong đó bất kì hai đoạn thẳng nào có một điểm chung cũng không cùng nằm trên một đường thẳng.
1. Khái niệm đa giác đều
Đa giác
- Đa giác ABCDE là hình gồm các đoạn thẳng AB, BC, CD, DE và EA, trong đó bất kì hai đoạn thẳng nào có một điểm chung cũng không cùng nằm trên một đường thẳng.
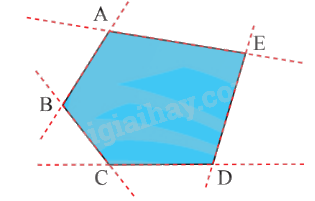
+ Các điểm A, B, C, D, E gọi là các đỉnh.
+ Các đoạn thẳng AB, BC, CD, DE, EA gọi là các cạnh.
+ Các góc \(\widehat {ABC},\widehat {BCD},\widehat {CDE},\widehat {DEA},\widehat {EAB}\) gọi là các góc của đa giác.
- Đa giác được gọi là đa giác lồi nếu nó luôn nằm về một phía của bất kì đường thẳng nào đi qua một cạnh của đa giác đó.
Đa giác đều
Đa giác đều là một đa giác lồi có các cạnh bằng nhau và các góc bằng nhau. |
Ví dụ: Một số hình đa giác đều thường gặp trong hình học:

- Đa giác đều có số cạnh bằng n được gọi là n-giác đều.
- Với n lần lượt bằng 3, 4, 5, 6, 8, ... ta có tam giác đều, tứ giác đều (hình vuông), ngũ giác đều, lục giác đều, bát giác đều,...
- Từ nay, khi nói đến đa giác mà không chú thích gì thêm, ta hiểu đó là đa giác lồi.
Chú ý: Người ta chứng minh được ứng với mỗi đa giác đều có một điểm O cách đều tất cả các đỉnh của đa giác. Điểm O gọi là tâm của đa giác đó.
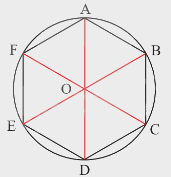
2. Phép quay
Khái niệm phép quay
Phép quay thuận chiều \(\alpha ^\circ \) (0° < \(\alpha ^\circ \) < 360°) tâm O giữ nguyên điểm O, biến điểm A khác điểm O thành điểm B thuộc đường tròn (O; OA) sao cho tia OA quay thuận chiều kim đồng hồ đến tia OB thì điểm A tạo nên cung AB có số đo \(\alpha ^\circ \) (hình a). Định nghĩa tương tự cho phép quay ngược chiều \(\alpha ^\circ \) tâm O (hình b). Chú ý: Phép quay 0° và phép quay 360° giữ nguyên mọi điểm.
|
Phép quay giữ nguyên hình đa giác đều
- Ta coi mỗi phép quay tâm O biến O thành chính nó. - Nếu một phép quay biến các điểm M trên hình ℋ thành các điểm M’ thì các điểm M’ tạo thành hình ℋ’. Khi đó, ta nói phép quay biến hình thành hình ℋ’. Nếu hình ℋ’ trùng với hình ℋ thì ta nói phép quay biến hình ℋ thành chính nó. |
Ví dụ:
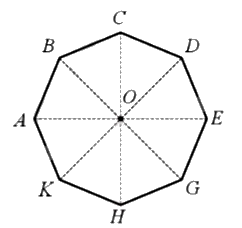
Phép quay thuận chiều \(45^\circ \) tâm O biến điểm A thành điểm B thì phép quay đó biến các điểm C, D, H, K tương ứng thành các điểm D, E, K, A.
3. Hình phẳng đều trong thực tế
Ví dụ: Một số hình phẳng đều trong thực tế:

Trong chương trình Toán 9, kiến thức về đa giác đều và phép quay đóng vai trò quan trọng, không chỉ giúp học sinh hiểu sâu hơn về hình học mà còn là nền tảng cho các kiến thức nâng cao ở các lớp học tiếp theo. Bài viết này sẽ cung cấp một cái nhìn toàn diện về lý thuyết này, bao gồm định nghĩa, tính chất, và ứng dụng thực tế.
1. Định nghĩa: Đa giác đều là đa giác có tất cả các cạnh bằng nhau và tất cả các góc bằng nhau.
2. Tính chất:
3. Ví dụ: Tam giác đều, hình vuông, ngũ giác đều, lục giác đều,...
1. Định nghĩa: Phép quay tâm O với góc α (α đo bằng độ, chiều dương là chiều ngược chiều kim đồng hồ) là phép biến hình biến mỗi điểm M thành điểm M' sao cho OM = OM' và góc MOM' = α.
2. Tính chất:
3. Biểu thức tọa độ: Nếu điểm M(x; y) và tâm quay O(a; b), góc quay α thì tọa độ điểm M'(x'; y') được tính theo công thức:
x' = a + (x - a)cosα - (y - b)sinα
y' = b + (x - a)sinα + (y - b)cosα
Đa giác đều có tính đối xứng cao, và phép quay đóng vai trò quan trọng trong việc thể hiện tính đối xứng đó. Ví dụ, một hình vuông có thể được tạo ra bằng cách quay một tam giác vuông một góc 90 độ quanh tâm của nó.
Ví dụ: Xét hình vuông ABCD tâm O. Khi quay hình vuông ABCD quanh tâm O một góc 90 độ theo chiều dương, ta được hình vuông A'B'C'D' trùng với hình vuông ABCD.
Bài 1: Cho tam giác đều ABC có cạnh bằng a. Tính bán kính đường tròn ngoại tiếp và đường tròn nội tiếp của tam giác ABC.
Bài 2: Cho hình vuông ABCD có cạnh bằng a. Xác định tâm đối xứng và các trục đối xứng của hình vuông ABCD.
Bài 3: Cho điểm M(2; 3) và tâm quay O(1; 1). Tính tọa độ điểm M' khi quay điểm M quanh tâm O một góc 45 độ theo chiều dương.
Lý thuyết Đa giác đều và phép quay là một phần quan trọng của chương trình Toán 9. Việc nắm vững kiến thức này không chỉ giúp học sinh giải quyết các bài toán hình học một cách hiệu quả mà còn là nền tảng cho các kiến thức toán học nâng cao hơn. Hy vọng bài viết này đã cung cấp cho bạn những thông tin hữu ích và giúp bạn hiểu rõ hơn về chủ đề này.