Giaitoan.edu.vn xin giới thiệu lời giải chi tiết bài tập 6 trang 50 SGK Toán 9 tập 2 - Chân trời sáng tạo. Bài viết này sẽ giúp học sinh nắm vững kiến thức, hiểu rõ phương pháp giải và tự tin làm bài tập.
Chúng tôi luôn cố gắng cung cấp những lời giải chính xác, dễ hiểu và phù hợp với trình độ của học sinh. Hãy cùng giaitoan.edu.vn khám phá lời giải bài tập này ngay nhé!
Số bàn thắng một đội bóng ghi được trong 26 Trận đấu của Giải vô địch quốc gia được ghi lại như sau: a) Hãy lập bảng tần số và tần số tương đối cho bảng số liệu trên. b) Hãy vẽ biểu đồ quạt tròn mô tả tần số tương đối của bảng số liệu trên.
Đề bài
Số bàn thắng một đội bóng ghi được trong 26 Trận đấu của Giải vô địch quốc gia được ghi lại như sau:

a) Hãy lập bảng tần số và tần số tương đối cho bảng số liệu trên.
b) Hãy vẽ biểu đồ quạt tròn mô tả tần số tương đối của bảng số liệu trên.
Video hướng dẫn giải
Phương pháp giải - Xem chi tiết
- Xác định cỡ mẫu bằng cách lấy cột dọc nhân cột ngang,
- Lập bảng tần số theo: Bảng tần số biểu diễn tần số của mỗi giá trị trong mẫu dữ liệu gồm hai dòng, dòng trên ghi các giá trị khác nhau của mẫu dữ liệu, dòng dưới ghi các tần số tương ứng với mỗi giá trị đó.
- Tần số tương đối của một giá trị x trong mẫu dữ liệu được tính theo công thức \(f = \frac{m}{N}.100\% \), trong đó m là tần số của x và N là cỡ mẫu.
- Vẽ biểu đồ tần số tương đối dạng hình quạt tròn: hình quạt tròn biểu thị tần số tương đối a% có số đo cung tương ứng a% . 360o = 3,6ao
Lời giải chi tiết
a) Ta được bảng sau:
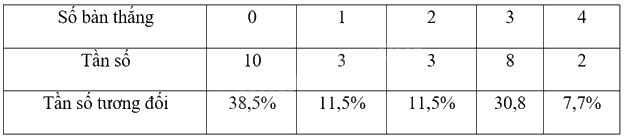
b) Biểu đồ quạt tròn mô tả tần số tương đối của bảng số liệu trên
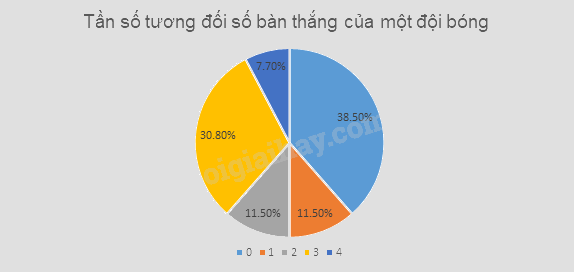
Bài tập 6 trang 50 SGK Toán 9 tập 2 - Chân trời sáng tạo thuộc chương trình học Toán 9, tập trung vào việc vận dụng kiến thức về hàm số bậc nhất và hàm số bậc hai để giải quyết các bài toán thực tế. Bài tập này yêu cầu học sinh phải hiểu rõ các khái niệm về hệ số góc, giao điểm của đồ thị hàm số và cách xác định phương trình đường thẳng.
Trước khi bắt đầu giải bài tập, chúng ta cần đọc kỹ đề bài và xác định rõ yêu cầu của bài toán. Trong bài tập 6 trang 50, yêu cầu chính là tìm phương trình đường thẳng đi qua hai điểm cho trước hoặc xác định giao điểm của hai đường thẳng.
Để giải bài tập này, chúng ta có thể sử dụng các phương pháp sau:
(Ở đây sẽ là lời giải chi tiết cho từng câu của bài tập 6, bao gồm các bước giải, giải thích và kết luận. Ví dụ:)
Câu a: Tìm phương trình đường thẳng đi qua hai điểm A(1; 2) và B(3; 4).
Câu b: Tìm giao điểm của hai đường thẳng y = 2x + 1 và y = -x + 4.
Để nắm vững kiến thức về hàm số bậc nhất và bậc hai, các em nên luyện tập thêm các bài tập tương tự trong SGK và các tài liệu tham khảo khác. Ngoài ra, các em có thể tham khảo các bài giảng online hoặc tìm kiếm sự giúp đỡ của giáo viên và bạn bè.
Hàm số bậc nhất và bậc hai có rất nhiều ứng dụng trong thực tế, ví dụ như:
Bài tập 6 trang 50 SGK Toán 9 tập 2 - Chân trời sáng tạo là một bài tập quan trọng giúp học sinh củng cố kiến thức về hàm số bậc nhất và bậc hai. Hy vọng với lời giải chi tiết và hướng dẫn giải bài tập này, các em sẽ học tập tốt hơn và đạt kết quả cao trong môn Toán.
| Khái niệm | Giải thích |
|---|---|
| Hàm số bậc nhất | Hàm số có dạng y = ax + b, trong đó a và b là các số thực. |
| Hàm số bậc hai | Hàm số có dạng y = ax2 + bx + c, trong đó a, b và c là các số thực. |