Chào mừng bạn đến với giaitoan.edu.vn, nơi cung cấp lời giải chi tiết và dễ hiểu cho các bài tập Toán 9 tập 2. Bài viết này sẽ hướng dẫn bạn giải bài tập 2 trang 97 sách giáo khoa Toán 9 tập 2, chương trình Chân trời sáng tạo.
Chúng tôi hiểu rằng việc giải toán đôi khi có thể gặp khó khăn. Vì vậy, chúng tôi đã biên soạn lời giải một cách cẩn thận, kèm theo các bước giải chi tiết và giải thích rõ ràng để giúp bạn nắm vững kiến thức.
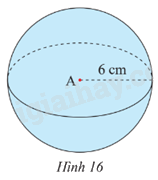
Quan sát hình cầu ở Hình 16. Hãy cho biết tâm, bán kính, diện tích mặt cầu và thể tích của hình cầu đó.
Đề bài
Quan sát hình cầu ở Hình 16. Hãy cho biết tâm, bán kính, diện tích mặt cầu và thể tích của hình cầu đó.
Video hướng dẫn giải
Phương pháp giải - Xem chi tiết
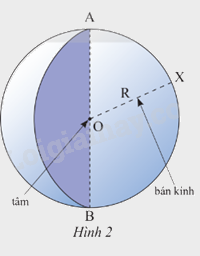
- Khi quay nửa hình tròn tâm O, bán kính R một vòng quanh đường kính AB cố định ta được một hình cầu tâm O, bán kính R.
Khi đó, nửa đường tròn quét thành một mặt cầu. Ta cũng gọi O và R lần lượt là tâm và bán kính của mặt cầu đó.
Đoạn thẳng đi qua tâm của hình cầu với hai đầu mút nằm trên mặt cầu gọi là đường kính của hình cầu.
- Công thức thể tích của hình cầu có bán kính R là: V = \(\frac{4}{3}\pi {R^3}\).
- Diện tích mặt cầu là: S = \(4\pi {R^2}\)
Lời giải chi tiết
Tâm của hình cầu là A.
Bán kính có độ dài 6 cm.
Diện tích mặt cầu là: S = \(4\pi {R^2}\) = 144 \(\pi \)(cm2).
Thể tích của hình cầu là: V = \(\frac{4}{3}\pi {R^3} = 288\pi \) (cm3).
Bài tập 2 trang 97 SGK Toán 9 tập 2 thuộc chương trình Chân trời sáng tạo yêu cầu học sinh vận dụng kiến thức về hàm số bậc hai để giải quyết các bài toán thực tế. Để giải bài tập này một cách hiệu quả, chúng ta cần nắm vững các khái niệm cơ bản như:
Trước khi bắt đầu giải bài tập, chúng ta cần đọc kỹ đề bài và xác định rõ yêu cầu của bài toán. Trong bài tập 2 trang 97, đề bài thường yêu cầu chúng ta:
Để giúp bạn hiểu rõ hơn về cách giải bài tập 2 trang 97, chúng ta sẽ cùng nhau phân tích một ví dụ cụ thể. Giả sử đề bài yêu cầu chúng ta tìm tọa độ đỉnh của parabol y = x2 - 4x + 3.
Bước 1: Xác định hệ số a, b, c
Trong hàm số y = x2 - 4x + 3, ta có a = 1, b = -4, c = 3.
Bước 2: Tính hoành độ đỉnh
Hoành độ đỉnh của parabol được tính theo công thức x0 = -b / 2a. Thay a = 1 và b = -4 vào công thức, ta được:
x0 = -(-4) / (2 * 1) = 2
Bước 3: Tính tung độ đỉnh
Tung độ đỉnh của parabol được tính theo công thức y0 = f(x0). Thay x0 = 2 vào hàm số y = x2 - 4x + 3, ta được:
y0 = 22 - 4 * 2 + 3 = 4 - 8 + 3 = -1
Bước 4: Kết luận
Vậy tọa độ đỉnh của parabol y = x2 - 4x + 3 là (2; -1).
Ngoài việc tìm tọa độ đỉnh, bài tập 2 trang 97 còn có thể xuất hiện các dạng bài tập khác như:
Để giải bài tập 2 trang 97 một cách hiệu quả, bạn có thể áp dụng một số mẹo sau:
Bài tập 2 trang 97 SGK Toán 9 tập 2 - Chân trời sáng tạo là một bài tập quan trọng giúp bạn củng cố kiến thức về hàm số bậc hai. Hy vọng rằng với hướng dẫn chi tiết và các mẹo giải bài tập hiệu quả mà chúng tôi đã cung cấp, bạn sẽ tự tin giải quyết bài tập này một cách dễ dàng.
Giaitoan.edu.vn luôn đồng hành cùng bạn trên con đường chinh phục môn Toán. Chúc bạn học tập tốt!