Giải bài tập 3 trang 69 SGK Toán 9 tập 2 - Chân trời sáng tạo

Giaitoan.edu.vn xin giới thiệu lời giải chi tiết bài tập 3 trang 69 SGK Toán 9 tập 2 - Chân trời sáng tạo. Bài viết này sẽ giúp học sinh nắm vững kiến thức, hiểu rõ phương pháp giải và tự tin làm bài tập.

Chúng tôi cung cấp đáp án chính xác, dễ hiểu, kèm theo các bước giải cụ thể, giúp bạn dễ dàng theo dõi và áp dụng vào các bài tập tương tự. Hãy cùng giaitoan.edu.vn khám phá lời giải chi tiết ngay sau đây!

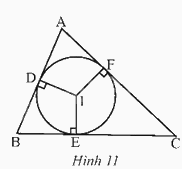
Cho tam giác ABC ngoại tiếp đường tròn (I). Gọi D, E, F lần lượt là các tiếp điểm của đường tròn (I) với các cạnh AB, BC, AC (Hình 11). a) Chứng minh 2AD = AB + AC – BC. b) Tìm các hệ thức tương tự như ở câu a.

Đề bài

Cho tam giác ABC ngoại tiếp đường tròn (I). Gọi D, E, F lần lượt là các tiếp điểm của đường tròn (I) với các cạnh AB, BC, AC (Hình 11).

a) Chứng minh 2AD = AB + AC – BC.

b) Tìm các hệ thức tương tự như ở câu a.

Giải bài tập 3 trang 69 SGK Toán 9 tập 2 - Chân trời sáng tạo 1

Video hướng dẫn giải

Phương pháp giải - Xem chi tiết Giải bài tập 3 trang 69 SGK Toán 9 tập 2 - Chân trời sáng tạo 2

Sử dụng tính chất hai tiếp tuyến cắt nhau suy ra AD = AF; BD = BE; FC = EC rồi thay vào hệ thức 2AD = AB + AC – BC để chứng minh.

Lời giải chi tiết

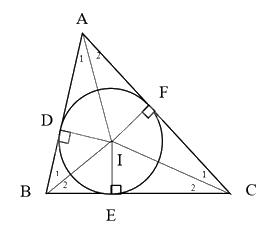
Giải bài tập 3 trang 69 SGK Toán 9 tập 2 - Chân trời sáng tạo 3

a) Ta có D, E, F lần lượt là các tiếp điểm của đường tròn (I) với các cạnh AB, BC, AC nên tính chất hai tiếp tuyến bằng nhau, ta có:

\(AD = AF; CF = CE; BD = BE\) (1)

Ta có:

\(AB + AC – BC = (AD + BD) + (AF + FC) – (BE + EC) \)

\(= AD + BD + AF + FC – BE - EC\) (2)

Từ (1) và (2) suy ra

\(AB + AC – BC = AD + BE + AD + EC – BE – EC\)

\(= (AD + AD) + (BE - BE) + (CE - CE) = 2AD\)

b) Các hệ thức tương tự như ở câu a:

\(2AF = AB + AC – BC\);

\(2BD = 2BE = AB + BC – AC\);

\(2EC = 2FC = AC + BC – AB\).

Làm chủ Toán 9, tự tin vào phòng thi! Đừng bỏ lỡ Giải bài tập 3 trang 69 SGK Toán 9 tập 2 - Chân trời sáng tạo đặc sắc thuộc chuyên mục giải bài tập toán 9 trên nền tảng soạn toán. Với bộ bài tập toán thcs được biên soạn chuyên sâu, bám sát cấu trúc đề thi và chương trình sách giáo khoa mới nhất, đây chính là công cụ đắc lực giúp các em tối ưu hóa ôn luyện, củng cố kiến thức vững chắc và thuần thục mọi dạng bài thi khó nhằn. Phương pháp học trực quan, khoa học sẽ mang lại hiệu quả vượt trội, giúp con bạn chinh phục mọi thử thách một cách dễ dàng.

Giải bài tập 3 trang 69 SGK Toán 9 tập 2 - Chân trời sáng tạo: Hướng dẫn chi tiết

Bài tập 3 trang 69 SGK Toán 9 tập 2 - Chân trời sáng tạo thuộc chương trình học Toán 9, tập trung vào việc vận dụng các kiến thức về hàm số bậc hai để giải quyết các bài toán thực tế. Để giải quyết bài tập này một cách hiệu quả, học sinh cần nắm vững các khái niệm cơ bản như:

Định nghĩa hàm số bậc hai
Đồ thị hàm số bậc hai
Các yếu tố của đồ thị hàm số bậc hai (đỉnh, trục đối xứng, giao điểm với các trục tọa độ)
Ứng dụng của hàm số bậc hai trong việc giải quyết các bài toán thực tế

Phân tích đề bài và tìm hướng giải

Trước khi bắt đầu giải bài tập, học sinh cần đọc kỹ đề bài, xác định rõ yêu cầu của bài toán và các dữ kiện đã cho. Sau đó, cần phân tích đề bài để tìm ra hướng giải phù hợp. Đối với bài tập 3 trang 69, học sinh cần xác định được hàm số bậc hai cần xét và các điều kiện ràng buộc của bài toán.

Lời giải chi tiết bài tập 3 trang 69

Để giúp học sinh hiểu rõ hơn về cách giải bài tập này, chúng tôi xin trình bày lời giải chi tiết như sau:

Đề bài: (Giả sử đề bài là: Tìm giá trị của m để hàm số y = x² - 2mx + m + 2 có giá trị nhỏ nhất bằng 1)

Giải:

Xác định đỉnh của parabol: Hàm số y = x² - 2mx + m + 2 là một hàm số bậc hai có dạng y = ax² + bx + c, với a = 1, b = -2m, c = m + 2. Tọa độ đỉnh của parabol là:

x_đỉnh = -b / 2a = -(-2m) / (2 * 1) = m
y_đỉnh = -Δ / 4a = -((-2m)² - 4 * 1 * (m + 2)) / (4 * 1) = -(4m² - 4m - 8) / 4 = -m² + m + 2

Áp dụng điều kiện giá trị nhỏ nhất: Theo đề bài, giá trị nhỏ nhất của hàm số là 1, tức là y_đỉnh = 1. Do đó, ta có phương trình:

-m² + m + 2 = 1

Giải phương trình bậc hai: Giải phương trình -m² + m + 2 = 1, ta được:

-m² + m + 1 = 0
m² - m - 1 = 0
Sử dụng công thức nghiệm của phương trình bậc hai, ta có:
m = (1 ± √(1² - 4 * 1 * (-1))) / (2 * 1) = (1 ± √5) / 2

Kết luận: Vậy, giá trị của m cần tìm là m = (1 + √5) / 2 hoặc m = (1 - √5) / 2.

Lưu ý khi giải bài tập

Khi giải bài tập về hàm số bậc hai, học sinh cần lưu ý một số điểm sau:

Nắm vững các khái niệm cơ bản về hàm số bậc hai.
Hiểu rõ các yếu tố của đồ thị hàm số bậc hai và cách xác định chúng.
Luyện tập thường xuyên để làm quen với các dạng bài tập khác nhau.
Kiểm tra lại kết quả sau khi giải bài tập để đảm bảo tính chính xác.

Ứng dụng của hàm số bậc hai trong thực tế

Hàm số bậc hai có nhiều ứng dụng trong thực tế, ví dụ như:

Tính quỹ đạo của vật ném.
Xác định hình dạng của các vật thể có mặt cắt ngang là parabol.
Giải quyết các bài toán tối ưu hóa trong kinh tế và kỹ thuật.

Tổng kết

Bài tập 3 trang 69 SGK Toán 9 tập 2 - Chân trời sáng tạo là một bài tập quan trọng giúp học sinh củng cố kiến thức về hàm số bậc hai. Hy vọng rằng, với lời giải chi tiết và các lưu ý trên, học sinh sẽ tự tin hơn khi giải quyết các bài tập tương tự. Chúc các em học tập tốt!