Giải bài tập 4 trang 80 SGK Toán 9 tập 2 - Chân trời sáng tạo

Bài tập 4 trang 80 SGK Toán 9 tập 2 thuộc chương trình Toán 9 Chân trời sáng tạo là một bài tập quan trọng giúp học sinh rèn luyện kỹ năng giải bài toán thực tế liên quan đến hàm số bậc nhất. Bài tập này đòi hỏi học sinh phải nắm vững kiến thức về cách xác định hệ số góc, đường thẳng song song và các ứng dụng của hàm số bậc nhất.

Giaitoan.edu.vn xin giới thiệu lời giải chi tiết, dễ hiểu bài tập 4 trang 80 SGK Toán 9 tập 2, giúp các em học sinh hiểu rõ phương pháp giải và tự tin làm bài tập.

Cho đường tròn (O; R). a) Vẽ hình tam giác đều, hình vuông, hình lục giác đều có các đỉnh nằm trên (O; R). b) Tính các cạnh của các hình vừa vẽ theo R.

Đề bài

Cho đường tròn (O; R).

a) Vẽ hình tam giác đều, hình vuông, hình lục giác đều có các đỉnh nằm trên (O; R).

b) Tính các cạnh của các hình vừa vẽ theo R.

Video hướng dẫn giải

Phương pháp giải - Xem chi tiết Giải bài tập 4 trang 80 SGK Toán 9 tập 2 - Chân trời sáng tạo 1

- Đọc kĩ dữ kiện đề bài để vẽ hình.

- Dựa vào: Đa giác lồi có các cạnh bằng nhau và các góc bằng nhau gọi là đa giác đều.

- Dựa vào đường tròn ngoại tiếp tam giác đều cạnh a có tâm là trọng tâm của tam giác và bán kính bằng \(\frac{{a\sqrt 3 }}{3}\).

- Dựa vào: Đường tròn ngoại tiếp hình chữ nhật, hình vuông có tâm là giao điểm của hai đường chéo và có bán kính bằng nửa đường chéo.

Lời giải chi tiết

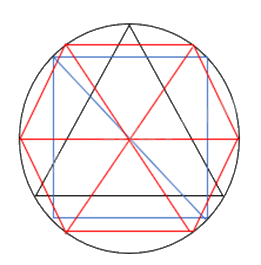
Giải bài tập 4 trang 80 SGK Toán 9 tập 2 - Chân trời sáng tạo 2

b) Tam giác đều nội tiếp đường tròn nên ta có:

R = \(\frac{{a\sqrt 3 }}{3}\) (a là độ dài cạnh tam giác đều)

Suy ra a = \(\frac{{3R}}{{\sqrt 3 }} = R\sqrt 3 \)

Hình vuông nội tiếp đường tròn nên ta có:

\(R = \frac{d}{2}\) (d là đường chéo của hình vuông)

Suy ra d = 2R. Gọi x là độ dài cạnh hình vuông hay \(\sqrt {{x^2} + {x^2}} = 2R\) suy ra \(x\sqrt 2 = 2R\)

Hay x = \(\frac{{2R}}{{\sqrt 2 }} = R\sqrt 2 \)

Trong lục giác đều có khoảng cách từ tâm đến các đỉnh là bằng nhau (= R); các góc ở tâm đều bằng 60^o nên lục giác đều gồm 6 tam giác đều.

Suy ra độ dài cạnh của lục giác đều là R.

Làm chủ Toán 9, tự tin vào phòng thi! Đừng bỏ lỡ Giải bài tập 4 trang 80 SGK Toán 9 tập 2 - Chân trời sáng tạo đặc sắc thuộc chuyên mục bài tập toán 9 trên nền tảng học toán. Với bộ bài tập toán thcs được biên soạn chuyên sâu, bám sát cấu trúc đề thi và chương trình sách giáo khoa mới nhất, đây chính là công cụ đắc lực giúp các em tối ưu hóa ôn luyện, củng cố kiến thức vững chắc và thuần thục mọi dạng bài thi khó nhằn. Phương pháp học trực quan, khoa học sẽ mang lại hiệu quả vượt trội, giúp con bạn chinh phục mọi thử thách một cách dễ dàng.

Giải bài tập 4 trang 80 SGK Toán 9 tập 2 - Chân trời sáng tạo: Hướng dẫn chi tiết

Bài tập 4 trang 80 SGK Toán 9 tập 2 Chân trời sáng tạo yêu cầu học sinh giải quyết một bài toán thực tế liên quan đến hàm số bậc nhất. Để giải bài tập này một cách hiệu quả, chúng ta cần nắm vững các kiến thức cơ bản về hàm số bậc nhất, bao gồm:

Định nghĩa hàm số bậc nhất: Hàm số bậc nhất có dạng y = ax + b, trong đó a và b là các số thực, a ≠ 0.
Hệ số góc: a là hệ số góc của đường thẳng biểu diễn hàm số bậc nhất. Hệ số góc cho biết độ dốc của đường thẳng.
Đường thẳng song song: Hai đường thẳng y = a₁x + b₁ và y = a₂x + b₂ song song với nhau khi và chỉ khi a₁ = a₂ và b₁ ≠ b₂.
Ứng dụng của hàm số bậc nhất: Hàm số bậc nhất được sử dụng để mô tả các mối quan hệ tuyến tính trong thực tế, chẳng hạn như quãng đường đi được của một vật chuyển động đều, sự thay đổi nhiệt độ theo thời gian, v.v.

Phân tích đề bài

Trước khi bắt đầu giải bài tập, chúng ta cần đọc kỹ đề bài và xác định rõ các thông tin quan trọng. Đề bài thường cung cấp các dữ kiện về mối quan hệ giữa các đại lượng, các điều kiện ràng buộc và yêu cầu của bài toán. Việc phân tích đề bài một cách cẩn thận sẽ giúp chúng ta xây dựng được phương án giải phù hợp.

Lời giải chi tiết bài tập 4 trang 80 SGK Toán 9 tập 2

(Ở đây sẽ là lời giải chi tiết của bài tập 4 trang 80, bao gồm các bước giải, giải thích rõ ràng và kết luận. Ví dụ:)

Bài tập: Một người đi xe đạp từ A đến B với vận tốc 12 km/h. Hỏi sau bao lâu người đó đến B, biết rằng quãng đường AB dài 36 km?

Giải:

Gọi t là thời gian người đó đi từ A đến B (t tính bằng giờ).
Quãng đường AB được tính bằng công thức: S = v * t, trong đó S là quãng đường, v là vận tốc và t là thời gian.
Thay số vào công thức, ta có: 36 = 12 * t
Giải phương trình trên, ta được: t = 36 / 12 = 3
Vậy người đó đi từ A đến B mất 3 giờ.

Các dạng bài tập tương tự

Ngoài bài tập 4 trang 80, SGK Toán 9 tập 2 còn có nhiều bài tập tương tự về hàm số bậc nhất. Các bài tập này thường yêu cầu học sinh:

Xác định hệ số góc và đường thẳng song song.
Giải các bài toán thực tế liên quan đến hàm số bậc nhất.
Vẽ đồ thị của hàm số bậc nhất.
Tìm giao điểm của hai đường thẳng.

Mẹo giải bài tập hàm số bậc nhất

Để giải các bài tập về hàm số bậc nhất một cách hiệu quả, bạn có thể áp dụng một số mẹo sau:

Nắm vững định nghĩa và các tính chất của hàm số bậc nhất.
Luyện tập giải nhiều bài tập khác nhau để làm quen với các dạng bài và phương pháp giải.
Sử dụng đồ thị để minh họa và kiểm tra kết quả.
Kiểm tra lại kết quả sau khi giải xong.

Kết luận

Bài tập 4 trang 80 SGK Toán 9 tập 2 - Chân trời sáng tạo là một bài tập quan trọng giúp học sinh củng cố kiến thức về hàm số bậc nhất và rèn luyện kỹ năng giải bài toán thực tế. Hy vọng với lời giải chi tiết và các mẹo giải bài tập trên, các em học sinh sẽ tự tin hơn khi làm bài tập Toán 9.