Chào mừng các em học sinh đến với chuyên mục giải bài tập Toán 9 tập 2 của giaitoan.edu.vn. Ở bài viết này, chúng tôi sẽ cung cấp lời giải chi tiết và dễ hiểu cho các bài tập trong mục 1 trang 52, 53, 54 sách giáo khoa Toán 9 tập 2 - Chân trời sáng tạo.
Mục tiêu của chúng tôi là giúp các em nắm vững kiến thức, rèn luyện kỹ năng giải toán và tự tin hơn trong các kỳ thi sắp tới.
Hộp thứ nhất có 1 viên bi xanh. Hộp thứ hai có một viên bi xanh và 1 viên bi đỏ. Bận Xuân lấy ra 1 viên bi từ hộp thứ nhất. Bạn Thu lấy ra 1 viên bi từ hộp thứ hai. a) Phép thử của bạn Xuân có bao nhiêu kết quả có thể xảy ra? b) Phép thử của bạn Thu có bao nhiêu kết quả có thể xảy ra?
Video hướng dẫn giải
Trả lời câu hỏi Thực hành 2 trang 54 SGK Toán 9 Chân trời sáng tạo
Xác định không gian mẫu của các phép thử sau:
a) Gieo 2 lần một đồng xu có 1 mặt xanh và 1 mặt đỏ.
b) Lấy ra một quả bóng từ một hộp chứa 3 quả bóng được đánh số 1; 2; 3, xem số, trả lại hộp rồi lấy ra 1 quả bóng từ hộp đó.
Phương pháp giải:
Dựa vào khái niệm không gian mẫu, kí hiệu là \(\Omega \), là tập hợp tất cả các kết quả có thể xảy ra của phép thử.
Lời giải chi tiết:
a) Kí hiệu (i;j) là kết quả gieo thứ nhất xuất hiện màu i, lần gieo thứ hai xuất hiện màu j. Không gian mẫu của phép thử là:
\(\Omega \) = {(xanh;xanh), (xanh;đỏ), (đỏ;xanh), (đỏ;đỏ)}
b) Không gian mẫu của phép thử là:
\(\Omega \) = {(1;1); (1;2); (1;3); (2;1); (2;2); (2;3); (3;1); (3;2); (3;3)}
Video hướng dẫn giải
Trả lời câu hỏi Hoạt động 1 trang 52 SGK Toán 9 Chân trời sáng tạo
Hộp thứ nhất có 1 viên bi xanh. Hộp thứ hai có một viên bi xanh và 1 viên bi đỏ. Bạn Xuân lấy ra 1 viên bi từ hộp thứ nhất. Bạn Thu lấy ra 1 viên bi từ hộp thứ hai.
a) Phép thử của bạn Xuân có bao nhiêu kết quả có thể xảy ra?
b) Phép thử của bạn Thu có bao nhiêu kết quả có thể xảy ra?
Phương pháp giải:
Dựa vào hộp thứ nhất chỉ có 1 viên bi xanh thì lấy ra chỉ có 1 cách, hộp thứ hai có 2 viên bi xanh và đỏ thì có 2 cách.
Lời giải chi tiết:
a) Phép thử của bạn Xuân có duy nhất 1 kết quả có thể xảy ra là 1 viên bi xanh
b) Phép thử của bạn Thu có 2 kết quả có thể xảy ra có thể là 1 viên bi xanh hoặc 1 viên bi đỏ.
Video hướng dẫn giải
Trả lời câu hỏi Thực hành 1 trang 54SGK Toán 9 Chân trời sáng tạo
Trong các hoạt động sau, hoạt động nào là phép thử ngẫu nhiên? Tại sao?
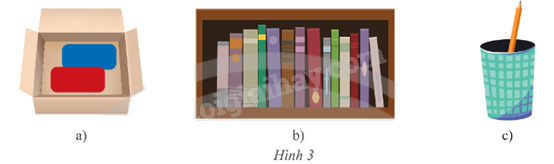
a) Chọn ra lần lượt hai tấm thẻ từ hộp có hai tấm thẻ như Hình 3a
b) Chọn bất kì 1 quyển sách từ giá như Hình 3b
c) Chọn 1 cây bút chì từ ống bút như Hình 3c.
Phương pháp giải:
Dựa vào khái niệm phép thử ngẫu nhiên: Các hoạt động mà ta không thể biết trước được kết quả của nó, nhưng biết tất cả các kết quả có thể xảy ra.
Lời giải chi tiết:
a) Chọn ra lần lượt hai tấm thẻ từ hộp có hai tấm thẻ như Hình 3a là phép thử ngẫu nhiên vì có 2 kết quả có thể xảy ra: lấy thẻ màu xanh trước rồi lấy thẻ màu đỏ hoặc ngược lại.
b) Chọn bất kì 1 quyển sách từ giá như Hình 3b là phép thử ngẫu nhiên vì ta không thể biết trước được kết quả của nó, nhưng biết tất cả 14 kết quả có thể xảy ra.
c) Chọn 1 cây bút chì từ ống bút như Hình 3c không là phép thử ngẫu nhiên vì ta biết chỉ có 1 kết quả xảy ra là lấy được 1 cây bút chì.
Video hướng dẫn giải
Trả lời câu hỏi Vận dụng 1 trang 54 SGK Toán 9 Chân trời sáng tạo
Xác định không gian mẫu của các phép thử trong Hoạt động khởi động (trang 52)
Một túi chứa 4 viên bi được đánh số như hình bên. Lấy ra ngẫu nhiên 1 viên bi từ túi.

Phương pháp giải:
Dựa vào khái niệm không gian mẫu, kí hiệu là \(\Omega \), là tập hợp tất cả các kết quả có thể xảy ra của phép thử.
Lời giải chi tiết:
Không gian mẫu của phép thử là:
\(\Omega \) = {1;2;3;4}
Video hướng dẫn giải
Trả lời câu hỏi Hoạt động 1 trang 52 SGK Toán 9 Chân trời sáng tạo
Hộp thứ nhất có 1 viên bi xanh. Hộp thứ hai có một viên bi xanh và 1 viên bi đỏ. Bạn Xuân lấy ra 1 viên bi từ hộp thứ nhất. Bạn Thu lấy ra 1 viên bi từ hộp thứ hai.
a) Phép thử của bạn Xuân có bao nhiêu kết quả có thể xảy ra?
b) Phép thử của bạn Thu có bao nhiêu kết quả có thể xảy ra?
Phương pháp giải:
Dựa vào hộp thứ nhất chỉ có 1 viên bi xanh thì lấy ra chỉ có 1 cách, hộp thứ hai có 2 viên bi xanh và đỏ thì có 2 cách.
Lời giải chi tiết:
a) Phép thử của bạn Xuân có duy nhất 1 kết quả có thể xảy ra là 1 viên bi xanh
b) Phép thử của bạn Thu có 2 kết quả có thể xảy ra có thể là 1 viên bi xanh hoặc 1 viên bi đỏ.
Video hướng dẫn giải
Trả lời câu hỏi Thực hành 1 trang 54SGK Toán 9 Chân trời sáng tạo
Trong các hoạt động sau, hoạt động nào là phép thử ngẫu nhiên? Tại sao?
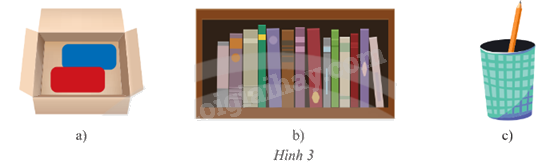
a) Chọn ra lần lượt hai tấm thẻ từ hộp có hai tấm thẻ như Hình 3a
b) Chọn bất kì 1 quyển sách từ giá như Hình 3b
c) Chọn 1 cây bút chì từ ống bút như Hình 3c.
Phương pháp giải:
Dựa vào khái niệm phép thử ngẫu nhiên: Các hoạt động mà ta không thể biết trước được kết quả của nó, nhưng biết tất cả các kết quả có thể xảy ra.
Lời giải chi tiết:
a) Chọn ra lần lượt hai tấm thẻ từ hộp có hai tấm thẻ như Hình 3a là phép thử ngẫu nhiên vì có 2 kết quả có thể xảy ra: lấy thẻ màu xanh trước rồi lấy thẻ màu đỏ hoặc ngược lại.
b) Chọn bất kì 1 quyển sách từ giá như Hình 3b là phép thử ngẫu nhiên vì ta không thể biết trước được kết quả của nó, nhưng biết tất cả 14 kết quả có thể xảy ra.
c) Chọn 1 cây bút chì từ ống bút như Hình 3c không là phép thử ngẫu nhiên vì ta biết chỉ có 1 kết quả xảy ra là lấy được 1 cây bút chì.
Video hướng dẫn giải
Trả lời câu hỏi Thực hành 2 trang 54 SGK Toán 9 Chân trời sáng tạo
Xác định không gian mẫu của các phép thử sau:
a) Gieo 2 lần một đồng xu có 1 mặt xanh và 1 mặt đỏ.
b) Lấy ra một quả bóng từ một hộp chứa 3 quả bóng được đánh số 1; 2; 3, xem số, trả lại hộp rồi lấy ra 1 quả bóng từ hộp đó.
Phương pháp giải:
Dựa vào khái niệm không gian mẫu, kí hiệu là \(\Omega \), là tập hợp tất cả các kết quả có thể xảy ra của phép thử.
Lời giải chi tiết:
a) Kí hiệu (i;j) là kết quả gieo thứ nhất xuất hiện màu i, lần gieo thứ hai xuất hiện màu j. Không gian mẫu của phép thử là:
\(\Omega \) = {(xanh;xanh), (xanh;đỏ), (đỏ;xanh), (đỏ;đỏ)}
b) Không gian mẫu của phép thử là:
\(\Omega \) = {(1;1); (1;2); (1;3); (2;1); (2;2); (2;3); (3;1); (3;2); (3;3)}
Video hướng dẫn giải
Trả lời câu hỏi Vận dụng 1 trang 54 SGK Toán 9 Chân trời sáng tạo
Xác định không gian mẫu của các phép thử trong Hoạt động khởi động (trang 52)
Một túi chứa 4 viên bi được đánh số như hình bên. Lấy ra ngẫu nhiên 1 viên bi từ túi.

Phương pháp giải:
Dựa vào khái niệm không gian mẫu, kí hiệu là \(\Omega \), là tập hợp tất cả các kết quả có thể xảy ra của phép thử.
Lời giải chi tiết:
Không gian mẫu của phép thử là:
\(\Omega \) = {1;2;3;4}
Mục 1 của chương trình Toán 9 tập 2 - Chân trời sáng tạo tập trung vào việc ôn tập và hệ thống hóa kiến thức về hàm số bậc nhất. Các bài tập trong mục này yêu cầu học sinh vận dụng các kiến thức đã học để giải quyết các bài toán thực tế, đồng thời rèn luyện kỹ năng tư duy logic và khả năng giải quyết vấn đề.
Bài 1 yêu cầu học sinh nhắc lại các khái niệm cơ bản về hàm số bậc nhất, bao gồm định nghĩa, dạng tổng quát, hệ số góc, và cách xác định hàm số.
Bài 2 yêu cầu học sinh xác định hàm số bậc nhất khi biết đồ thị của nó. Để làm được bài này, học sinh cần xác định được hai điểm thuộc đồ thị và sử dụng công thức tính hệ số góc.
Ví dụ: Cho đồ thị của hàm số bậc nhất đi qua hai điểm A(1; 2) và B(2; 4). Hãy xác định hàm số.
Bài 3 yêu cầu học sinh vẽ đồ thị của hàm số bậc nhất. Để vẽ đồ thị, học sinh cần xác định được ít nhất hai điểm thuộc đồ thị và nối chúng lại với nhau.
Ví dụ: Vẽ đồ thị của hàm số y = -x + 3.
Khi giải các bài tập về hàm số bậc nhất, học sinh cần lưu ý những điều sau:
Hàm số bậc nhất có nhiều ứng dụng trong thực tế, ví dụ như:
Hy vọng với lời giải chi tiết và những lưu ý trên, các em học sinh sẽ tự tin hơn khi giải các bài tập trong mục 1 trang 52, 53, 54 SGK Toán 9 tập 2 - Chân trời sáng tạo. Chúc các em học tập tốt!