Chào mừng các em học sinh đến với chuyên mục giải bài tập Toán 9 tập 1 của giaitoan.edu.vn. Ở bài viết này, chúng tôi sẽ cung cấp lời giải chi tiết và dễ hiểu cho các bài tập trong mục 3, trang 93, 94 và 95 của sách giáo khoa Toán 9 tập 1 - Chân trời sáng tạo.
Mục tiêu của chúng tôi là giúp các em nắm vững kiến thức, rèn luyện kỹ năng giải toán và tự tin hơn trong học tập.
Quan sát Hình 13. Hãy cho biết trong các góc (widehat {APB};widehat {AOB};widehat {AMB};widehat {AQB}), góc nào có đỉnh nằm trên đường tròn (O).
Video hướng dẫn giải
Trả lời câu hỏi Vận dụng 4 trang 93 SGK Toán 9 Chân trời sáng tạo
Cho hai điểm E và F nằm trên đường tròn (O). Có bao nhiêu góc nội tiếp chắn cung EF?
Phương pháp giải:
Dựa vào định nghĩa: góc nội tiếp là góc có đỉnh nằm trên đường tròn và hai cạnh chứa hai dây cung của đường tròn đó.
Lời giải chi tiết:
Có vô số góc nội tiếp chắn cung EF vì với mỗi một điểm khác E và F nằm trên đường tròn (O) ta có một góc nội tiếp.
Video hướng dẫn giải
Trả lời câu hỏi Vận dụng 5 trang 96 SGK Toán 9 Chân trời sáng tạo
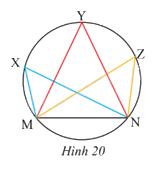
Một huấn luyện viên cho cầu thủ tập sút bóng vào cầu môn MN (Hình 20). Nếu bóng được đặt ở điểm X thì \(\widehat {MXN}\) gọi là góc sút từ vị trí X. Hãy so sánh các góc sút \(\widehat {MXN};\widehat {MYN};\widehat {MZN}\).
Phương pháp giải:
Dựa vào: Trong một đường tròn, các góc nội tiếp cùng chắn một cung thì bằng nhau.
Lời giải chi tiết:
Ta có \(\widehat {MXN};\widehat {MYN};\widehat {MZN}\) cùng chắn cung MN suy ra \(\widehat {MXN} = \widehat {MYN} = \widehat {MZN}\).
Video hướng dẫn giải
Trả lời câu hỏi Thực hành 5 trang 96SGK Toán 9 Chân trời sáng tạo
Cho ba điểm A, B, C nằm trên đường tròn (O) sao cho \(\widehat {AOB}\)= 50o; \(\widehat {BOC}\)= 30o, điểm B thuộc cung nhỏ AC. Gọi M, N lần lượt là hai điểm trên hai cung nhỏ \(\overset\frown{AB};\overset\frown{AC}\) và chia mỗi cung đó thành hai cung bằng nhau. Tìm số đo các góc sau:
a) \(\widehat {BCA};\widehat {BAC}\)
b) \(\widehat {MBA};\widehat {BAN}\)
Phương pháp giải:
- Dựa vào: Trong một đường tròn, góc nội tiếp nhỏ hơn hoặc bằng 90o có số đo bằng nửa số đo của góc ở tâm cùng chắn một cung để tìm \(\widehat {BCA};\widehat {BAC}\)
- Dựa vào số đo của cung nhỏ bằng số đo của góc ở tâm chắn cung đó để tìm sđ \(\overset\frown{AB}\); sđ\(\overset\frown{AC}\). Sau đó, dựa vào: Trong một đường tròn, góc nội tiếp nhỏ hơn hoặc bằng 90o có số đo bằng nửa số đo của góc ở tâm cùng chắn một cung để tìm \(\widehat {MBA};\widehat {BAN}\).
Lời giải chi tiết:
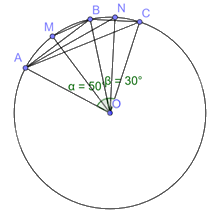
a) Ta có \(\widehat {BCA}\) và \(\widehat {AOB}\) lần lượt là góc nội tiếp và góc ở tâm cùng chắn cung AB
suy ra \(\widehat {BCA}\) = \(\frac{{\widehat {AOB}}}{2} = \frac{{{{50}^o}}}{2} = {25^o}\)
Ta có \(\widehat {BAC}\) và \(\widehat {BOC}\) lần lượt là góc nội tiếp và góc ở tâm cùng chắn cung BC
suy ra \(\widehat {BAC}\) = \(\frac{{\widehat {BOC}}}{2} = \frac{{{{30}^o}}}{2} = {15^o}\)
b) Ta có sđ \(\overset\frown{AB}\) = 50o ( bằng sđ của góc \(\widehat{AOB}\) cùng chắn \(\overset\frown{AB}\))
suy ra sđ \(\overset\frown{AM}=\)sđ \(\overset\frown{MB}\) = \(\frac{sđ\overset\frown{AB}}{2}=\frac{{{50}^{o}}}{2}={{25}^{o}}\) hay \(\widehat{MOA}=\widehat{MOB}={{25}^{o}}\)
Ta có \(\widehat {MBA}\) và \(\widehat {MOA}\) lần lượt là góc nội tiếp và góc ở tâm cùng chắn cung MA
suy ra \(\widehat {MBA}\) = \(\frac{{\widehat {MOA}}}{2} = \frac{{{{25}^o}}}{2} = 12,{5^o}\).
Ta có sđ \(\overset\frown{BC}\) = 30o ( bằng sđ của góc \(\widehat{BOC}\) cùng chắn \(\overset\frown{BC}\))
suy ra sđ \(\overset\frown{BN}=\)sđ \(\overset\frown{NC}\) = \(\frac{sđ\overset\frown{BC}}{2}=\frac{{{30}^{o}}}{2}={{15}^{o}}\) hay \(\widehat{BON}=\widehat{CON}={{15}^{o}}\)
Ta có \(\widehat {BAN}\) và \(\widehat {BON}\) lần lượt là góc nội tiếp và góc ở tâm cùng chắn cung BN
suy ra \(\widehat {BAN}\) = \(\frac{{\widehat {BON}}}{2} = \frac{{{{15}^o}}}{2} = 7,{5^o}\).
Video hướng dẫn giải
Trả lời câu hỏi Thực hành 4 trang 93 SGK Toán 9 Chân trời sáng tạo
Cho tam giác đều MNP có ba đỉnh nằm trên đường tròn (I). Hãy chỉ ra các góc nội tiếp của đường tròn (I) và tính số đo của các góc nội tiếp đó.
Phương pháp giải:
- Đọc dữ kiện đề bài để vẽ hình.
- Dựa vào định nghĩa: góc nội tiếp là góc có đỉnh nằm trên đường tròn và hai cạnh chứa hai dây cung của đường tròn đó.
Lời giải chi tiết:
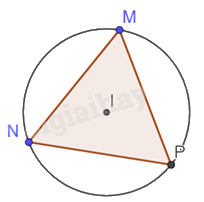
Các góc nội tiếp của đường tròn tâm I là \(\widehat {NMP};\widehat {MPN};\widehat {PNM}\)
Vì tam giác MNP đều nên \(\widehat {NMP} = \widehat {MPN} = \widehat {PNM} = {60^o}\).
Video hướng dẫn giải
Trả lời câu hỏi Hoạt động 5 trang 93SGK Toán 9 Chân trời sáng tạo
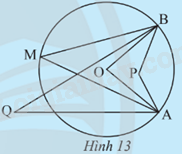
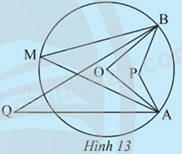
Quan sát Hình 13. Hãy cho biết trong các góc \(\widehat {APB};\widehat {AOB};\widehat {AMB};\widehat {AQB}\), góc nào có đỉnh nằm trên đường tròn (O).
Phương pháp giải:
Quan sát hình nêu nhận xét.
Lời giải chi tiết:
Theo Hình 13 thì góc có đỉnh nằm trên đường tròn là: \(\widehat {AMB}\).
Video hướng dẫn giải
Trả lời câu hỏi Hoạt động 6 trang 94SGK Toán 9 Chân trời sáng tạo
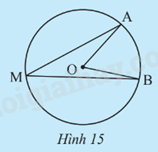
Quan sát Hình 15. Ta có góc nội tiếp \(\widehat {AMB}\) chắn cung AB trên đường tròn (O). Cho biết \(\widehat {AOB} = {60^o}\).
a) Tính số đo \(\overset\frown{AB}\).
b) Dùng thước đo góc để tìm số đo \(\widehat {AMB}\)
c) Có nhận xét gì về hai số đo của \(\widehat {AMB}\) và \(\overset\frown{AB}\).
Phương pháp giải:
- Dựa vào định nghĩa: Số đo cung nhỏ bằng số đo của góc ở tâm chắc cung đó
- Dùng thước đo góc \(\widehat {AMB}\) .
- Nhận xét hai số đo góc vừa tính được.
Lời giải chi tiết:
a) Ta có sđ\(\overset\frown{AB}\) bị chắn bởi góc ở tâm \(\widehat {AOB}\) có số đo bằng 60o suy ra sđ\(\overset\frown{AB}\) = 60o.
b) Dùng thức đo ta được \(\widehat {AMB}\)= 30o .
c) số đo của \(\widehat {AMB}\) = \(\frac{1}{2}\)sđ\(\overset\frown{AB}\).
Video hướng dẫn giải
Trả lời câu hỏi Hoạt động 5 trang 93SGK Toán 9 Chân trời sáng tạo
Quan sát Hình 13. Hãy cho biết trong các góc \(\widehat {APB};\widehat {AOB};\widehat {AMB};\widehat {AQB}\), góc nào có đỉnh nằm trên đường tròn (O).
Phương pháp giải:
Quan sát hình nêu nhận xét.
Lời giải chi tiết:
Theo Hình 13 thì góc có đỉnh nằm trên đường tròn là: \(\widehat {AMB}\).
Video hướng dẫn giải
Trả lời câu hỏi Thực hành 4 trang 93 SGK Toán 9 Chân trời sáng tạo
Cho tam giác đều MNP có ba đỉnh nằm trên đường tròn (I). Hãy chỉ ra các góc nội tiếp của đường tròn (I) và tính số đo của các góc nội tiếp đó.
Phương pháp giải:
- Đọc dữ kiện đề bài để vẽ hình.
- Dựa vào định nghĩa: góc nội tiếp là góc có đỉnh nằm trên đường tròn và hai cạnh chứa hai dây cung của đường tròn đó.
Lời giải chi tiết:
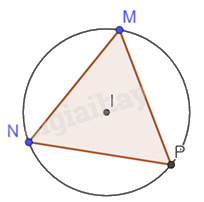
Các góc nội tiếp của đường tròn tâm I là \(\widehat {NMP};\widehat {MPN};\widehat {PNM}\)
Vì tam giác MNP đều nên \(\widehat {NMP} = \widehat {MPN} = \widehat {PNM} = {60^o}\).
Video hướng dẫn giải
Trả lời câu hỏi Vận dụng 4 trang 93 SGK Toán 9 Chân trời sáng tạo
Cho hai điểm E và F nằm trên đường tròn (O). Có bao nhiêu góc nội tiếp chắn cung EF?
Phương pháp giải:
Dựa vào định nghĩa: góc nội tiếp là góc có đỉnh nằm trên đường tròn và hai cạnh chứa hai dây cung của đường tròn đó.
Lời giải chi tiết:
Có vô số góc nội tiếp chắn cung EF vì với mỗi một điểm khác E và F nằm trên đường tròn (O) ta có một góc nội tiếp.
Video hướng dẫn giải
Trả lời câu hỏi Hoạt động 6 trang 94SGK Toán 9 Chân trời sáng tạo
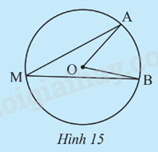
Quan sát Hình 15. Ta có góc nội tiếp \(\widehat {AMB}\) chắn cung AB trên đường tròn (O). Cho biết \(\widehat {AOB} = {60^o}\).
a) Tính số đo \(\overset\frown{AB}\).
b) Dùng thước đo góc để tìm số đo \(\widehat {AMB}\)
c) Có nhận xét gì về hai số đo của \(\widehat {AMB}\) và \(\overset\frown{AB}\).
Phương pháp giải:
- Dựa vào định nghĩa: Số đo cung nhỏ bằng số đo của góc ở tâm chắc cung đó
- Dùng thước đo góc \(\widehat {AMB}\) .
- Nhận xét hai số đo góc vừa tính được.
Lời giải chi tiết:
a) Ta có sđ\(\overset\frown{AB}\) bị chắn bởi góc ở tâm \(\widehat {AOB}\) có số đo bằng 60o suy ra sđ\(\overset\frown{AB}\) = 60o.
b) Dùng thức đo ta được \(\widehat {AMB}\)= 30o .
c) số đo của \(\widehat {AMB}\) = \(\frac{1}{2}\)sđ\(\overset\frown{AB}\).
Video hướng dẫn giải
Trả lời câu hỏi Thực hành 5 trang 96SGK Toán 9 Chân trời sáng tạo
Cho ba điểm A, B, C nằm trên đường tròn (O) sao cho \(\widehat {AOB}\)= 50o; \(\widehat {BOC}\)= 30o, điểm B thuộc cung nhỏ AC. Gọi M, N lần lượt là hai điểm trên hai cung nhỏ \(\overset\frown{AB};\overset\frown{AC}\) và chia mỗi cung đó thành hai cung bằng nhau. Tìm số đo các góc sau:
a) \(\widehat {BCA};\widehat {BAC}\)
b) \(\widehat {MBA};\widehat {BAN}\)
Phương pháp giải:
- Dựa vào: Trong một đường tròn, góc nội tiếp nhỏ hơn hoặc bằng 90o có số đo bằng nửa số đo của góc ở tâm cùng chắn một cung để tìm \(\widehat {BCA};\widehat {BAC}\)
- Dựa vào số đo của cung nhỏ bằng số đo của góc ở tâm chắn cung đó để tìm sđ \(\overset\frown{AB}\); sđ\(\overset\frown{AC}\). Sau đó, dựa vào: Trong một đường tròn, góc nội tiếp nhỏ hơn hoặc bằng 90o có số đo bằng nửa số đo của góc ở tâm cùng chắn một cung để tìm \(\widehat {MBA};\widehat {BAN}\).
Lời giải chi tiết:
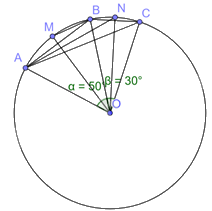
a) Ta có \(\widehat {BCA}\) và \(\widehat {AOB}\) lần lượt là góc nội tiếp và góc ở tâm cùng chắn cung AB
suy ra \(\widehat {BCA}\) = \(\frac{{\widehat {AOB}}}{2} = \frac{{{{50}^o}}}{2} = {25^o}\)
Ta có \(\widehat {BAC}\) và \(\widehat {BOC}\) lần lượt là góc nội tiếp và góc ở tâm cùng chắn cung BC
suy ra \(\widehat {BAC}\) = \(\frac{{\widehat {BOC}}}{2} = \frac{{{{30}^o}}}{2} = {15^o}\)
b) Ta có sđ \(\overset\frown{AB}\) = 50o ( bằng sđ của góc \(\widehat{AOB}\) cùng chắn \(\overset\frown{AB}\))
suy ra sđ \(\overset\frown{AM}=\)sđ \(\overset\frown{MB}\) = \(\frac{sđ\overset\frown{AB}}{2}=\frac{{{50}^{o}}}{2}={{25}^{o}}\) hay \(\widehat{MOA}=\widehat{MOB}={{25}^{o}}\)
Ta có \(\widehat {MBA}\) và \(\widehat {MOA}\) lần lượt là góc nội tiếp và góc ở tâm cùng chắn cung MA
suy ra \(\widehat {MBA}\) = \(\frac{{\widehat {MOA}}}{2} = \frac{{{{25}^o}}}{2} = 12,{5^o}\).
Ta có sđ \(\overset\frown{BC}\) = 30o ( bằng sđ của góc \(\widehat{BOC}\) cùng chắn \(\overset\frown{BC}\))
suy ra sđ \(\overset\frown{BN}=\)sđ \(\overset\frown{NC}\) = \(\frac{sđ\overset\frown{BC}}{2}=\frac{{{30}^{o}}}{2}={{15}^{o}}\) hay \(\widehat{BON}=\widehat{CON}={{15}^{o}}\)
Ta có \(\widehat {BAN}\) và \(\widehat {BON}\) lần lượt là góc nội tiếp và góc ở tâm cùng chắn cung BN
suy ra \(\widehat {BAN}\) = \(\frac{{\widehat {BON}}}{2} = \frac{{{{15}^o}}}{2} = 7,{5^o}\).
Video hướng dẫn giải
Trả lời câu hỏi Vận dụng 5 trang 96 SGK Toán 9 Chân trời sáng tạo
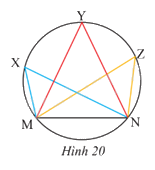
Một huấn luyện viên cho cầu thủ tập sút bóng vào cầu môn MN (Hình 20). Nếu bóng được đặt ở điểm X thì \(\widehat {MXN}\) gọi là góc sút từ vị trí X. Hãy so sánh các góc sút \(\widehat {MXN};\widehat {MYN};\widehat {MZN}\).
Phương pháp giải:
Dựa vào: Trong một đường tròn, các góc nội tiếp cùng chắn một cung thì bằng nhau.
Lời giải chi tiết:
Ta có \(\widehat {MXN};\widehat {MYN};\widehat {MZN}\) cùng chắn cung MN suy ra \(\widehat {MXN} = \widehat {MYN} = \widehat {MZN}\).
Mục 3 trong SGK Toán 9 tập 1 - Chân trời sáng tạo tập trung vào việc ôn tập và củng cố kiến thức về hàm số bậc nhất. Các bài tập trong mục này yêu cầu học sinh vận dụng các kiến thức đã học để giải quyết các bài toán thực tế, đồng thời rèn luyện kỹ năng tư duy logic và khả năng giải quyết vấn đề.
Bài 1 yêu cầu học sinh xác định các yếu tố của hàm số bậc nhất (hệ số a, b) và vẽ đồ thị của hàm số. Để giải bài tập này, học sinh cần nắm vững định nghĩa hàm số bậc nhất, các tính chất của hàm số và cách vẽ đồ thị hàm số.
Bài 2 đưa ra các bài toán thực tế liên quan đến hàm số bậc nhất, yêu cầu học sinh xây dựng phương trình hàm số và giải các bài toán đó. Ví dụ, bài toán có thể liên quan đến việc tính quãng đường đi được của một vật chuyển động đều, hoặc tính tiền điện tiêu thụ của một hộ gia đình.
Để giải bài tập này, học sinh cần:
Bài 3 cung cấp một số câu hỏi trắc nghiệm để kiểm tra mức độ hiểu bài của học sinh. Các câu hỏi trắc nghiệm thường tập trung vào các kiến thức cơ bản về hàm số bậc nhất, cách vẽ đồ thị hàm số và ứng dụng hàm số vào giải toán thực tế.
Giaitoan.edu.vn cung cấp lời giải chi tiết và dễ hiểu cho tất cả các bài tập trong mục 3, trang 93, 94 và 95 của SGK Toán 9 tập 1 - Chân trời sáng tạo. Lời giải của chúng tôi không chỉ cung cấp đáp án đúng mà còn giải thích rõ ràng các bước giải, giúp học sinh hiểu rõ bản chất của bài toán và tự tin hơn trong học tập.
Để hiểu rõ hơn về hàm số bậc nhất, học sinh có thể tham khảo thêm các tài liệu sau:
Hy vọng rằng với lời giải chi tiết và hướng dẫn giải của giaitoan.edu.vn, các em học sinh sẽ tự tin hơn trong việc giải các bài tập trong mục 3, trang 93, 94 và 95 của SGK Toán 9 tập 1 - Chân trời sáng tạo. Chúc các em học tập tốt!