Chào mừng các em học sinh đến với chuyên mục giải bài tập Toán 9 tập 2 của giaitoan.edu.vn. Chúng tôi xin giới thiệu lời giải chi tiết và dễ hiểu cho mục 1 trang 75, 76, 77 sách giáo khoa Toán 9 tập 2 - Chân trời sáng tạo.
Với đội ngũ giáo viên giàu kinh nghiệm, chúng tôi cam kết cung cấp những lời giải chính xác, đầy đủ và giúp các em hiểu sâu sắc kiến thức Toán học.
Có nhận xét gì về các cạnh và góc của mỗi đa giác sau?
Video hướng dẫn giải
Trả lời câu hỏi Vận dụng 1 trang 77 SGK Toán 9 Chân trời sáng tạo
Cho lục giác đều ABCDEF có M, N, P, Q, R, S lần lượt là trung điểm của các cạnh AB, BC, DE, EF, FA. Đa giác MNPQRS có là đa giác đều không? Vì sao?
Phương pháp giải:
- Đọc kĩ dữ kiện đề bài để vẽ hình
- Dựa vào: Đa giác lồi có các cạnh bằng nhau và các góc bằng nhau gọi là đa giác đều.
Lời giải chi tiết:
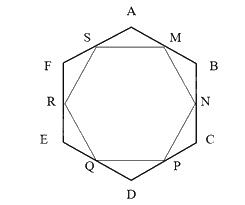
Do ABCDEF là lục giác đều nên:
\(\widehat A = \widehat B = \widehat C = \widehat D = \widehat E = \widehat F = {120^o}\).
- AB = BC = CD = DE = EF = FA.
Vì M, N, P, Q, R, S lần lượt là trung điểm của các cạnh AB, BC, DE, EF, FA.
Suy ra AM = MB = BN = NC = CP = PD = DQ = QE = ER = RF = FS = SA.
Xét \(\Delta \) SAM và \(\Delta \) MBN có:
\(\widehat A = \widehat B\) (chứng minh trên);
AM = BN (chứng minh trên);
SA = MB (chứng minh trên).
Suy ra \(\Delta \) SAM = \(\Delta \) MBN (c – g – c).
Do đó, SM = MN (hai cạnh tương ứng).
Chứng minh tương tự ta được: MN = NP, NP = PQ, QR = RS, RS = SM (1).
Vì AS = AM (chứng minh trên) suy ra \(\Delta \) ASM cân tại A.
suy ra \(\widehat {ASM} = \widehat {AMS}\) (tính chất tam giác cân)
Nên \(\widehat {ASM} = \widehat {AMS} = \frac{{{{180}^o} - \widehat A}}{2} = {30^o}\) (tổng 3 góc trong của tam giác).
Tương tự ta thu được:
\(\widehat {BMN} = \widehat {BNM} = \frac{{{{180}^o} - \widehat B}}{2} = 30\);
\(\widehat {CNP} = \widehat {CPN} = \frac{{{{180}^o} - \widehat C}}{2} = {30^o}\);
\(\widehat {DPQ} = \widehat {DQP} = \frac{{{{180}^o} - \widehat D}}{2} = {30^o}\);
\(\widehat {EQR} = \widehat {ERQ} = \frac{{{{180}^o} - \widehat E}}{2} = {30^o}\);.
\(\widehat {FRS} = \widehat {FSR} = \frac{{{{180}^o} - \widehat F}}{2} = {30^o}\)
Ta có:
\(\widehat {RSM} = {180^o} - \widehat {FRS} - \widehat {ASM} = {180^o} - {30^o} - {30^o} = {120^o}\)
Tương tự, ta được:
\(\widehat {AMN} = \widehat {MNP} = \widehat {NQP} = \widehat {PQR} = \widehat {QRS} = {120^o}\). (2)
Từ (1) và (2), suy ra MNPQRS là đa giác đều.
Video hướng dẫn giải
Trả lời câu hỏi Hoạt động 1 trang 75 SGK Toán 9 Chân trời sáng tạo
Có nhận xét gì về các cạnh và góc của mỗi đa giác sau?
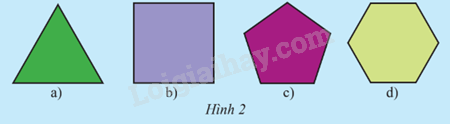
Phương pháp giải:
Nhìn hình nhận xét.
Lời giải chi tiết:
- Độ dài các cạnh của mỗi đa giác là bằng nhau.
- Số đo góc của mỗi đa giác là bằng nhau.
Video hướng dẫn giải
Trả lời câu hỏi Thực hành 1 trang 77 SGK Toán 9 Chân trời sáng tạo
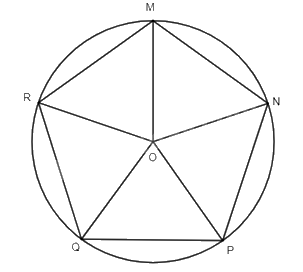
Cho đường tròn (O; R), trên đó lấy các điểm M, N, P, Q, R sao cho số đo các cung \(\overset\frown{MN},\overset\frown{NP},\overset\frown{PQ},\overset\frown{QR},\overset\frown{RM}\) bằng nhau. Đa giác MNPQR có là đa giác đều không? Vì sao?
Phương pháp giải:
- Đọc kĩ dữ kiện đề bài để vẽ hình
- Dựa vào: Đa giác lồi có các cạnh bằng nhau và các góc bằng nhau gọi là đa giác đều.
Lời giải chi tiết:
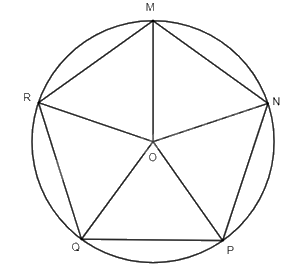
Các cung \(\overset\frown{MN}, \overset\frown{NP}, \overset\frown{PQ}, \overset\frown{QR}, \overset\frown{RM}\) chia đường tròn (O; R) thành 6 cung có số đo bằng nhau, suy ra số đo mỗi cung là 360o : 5 = 72o.
Ta có \(\widehat {MON}\) là góc nội tiếp chắn cung MN suy ra \(\widehat {MON}\) = 72o .
Xét \(\Delta \)MON, có: OM = ON = R suy ra \(\Delta \) MON cân tại O.
Suy ra \(\widehat {OMN} = \widehat {ONM}\) (tính chất tam giác cân)
Suy ra \(\widehat {OMN} = \widehat {ONM} = \frac{{{{180}^o} - \widehat {MON}}}{2} = {54^o}\).
Tương tự, ta có \(\widehat {OPN} = \widehat {ONP} = {54^o}\).
Suy ra \(\widehat {MPN} = \widehat {ONM} + \widehat {ONP} = {54^o} + {54^o} = {108^o}\).
Xét \(\Delta \) OMN và \(\Delta \) ONP có:
\(\widehat {MON} = \widehat {NOP}\);
OM = OP;
ON chung.
Suy ra \(\Delta \) OMN = \(\Delta \) ONP (c – g – c).
Do đó, MN = NP (hai cạnh tương ứng).
Chứng minh tương tự ta thu được ngũ giác MNPQR có các cạnh bằng nhau và các góc đều bằng nhau ( = 108o).
Vậy MNPQR là một đa giác đều.
Video hướng dẫn giải
Trả lời câu hỏi Hoạt động 1 trang 75 SGK Toán 9 Chân trời sáng tạo
Có nhận xét gì về các cạnh và góc của mỗi đa giác sau?
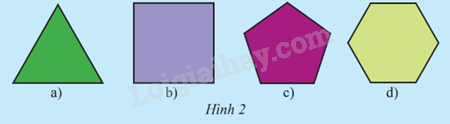
Phương pháp giải:
Nhìn hình nhận xét.
Lời giải chi tiết:
- Độ dài các cạnh của mỗi đa giác là bằng nhau.
- Số đo góc của mỗi đa giác là bằng nhau.
Video hướng dẫn giải
Trả lời câu hỏi Thực hành 1 trang 77 SGK Toán 9 Chân trời sáng tạo
Cho đường tròn (O; R), trên đó lấy các điểm M, N, P, Q, R sao cho số đo các cung \(\overset\frown{MN},\overset\frown{NP},\overset\frown{PQ},\overset\frown{QR},\overset\frown{RM}\) bằng nhau. Đa giác MNPQR có là đa giác đều không? Vì sao?
Phương pháp giải:
- Đọc kĩ dữ kiện đề bài để vẽ hình
- Dựa vào: Đa giác lồi có các cạnh bằng nhau và các góc bằng nhau gọi là đa giác đều.
Lời giải chi tiết:
Các cung \(\overset\frown{MN}, \overset\frown{NP}, \overset\frown{PQ}, \overset\frown{QR}, \overset\frown{RM}\) chia đường tròn (O; R) thành 6 cung có số đo bằng nhau, suy ra số đo mỗi cung là 360o : 5 = 72o.
Ta có \(\widehat {MON}\) là góc nội tiếp chắn cung MN suy ra \(\widehat {MON}\) = 72o .
Xét \(\Delta \)MON, có: OM = ON = R suy ra \(\Delta \) MON cân tại O.
Suy ra \(\widehat {OMN} = \widehat {ONM}\) (tính chất tam giác cân)
Suy ra \(\widehat {OMN} = \widehat {ONM} = \frac{{{{180}^o} - \widehat {MON}}}{2} = {54^o}\).
Tương tự, ta có \(\widehat {OPN} = \widehat {ONP} = {54^o}\).
Suy ra \(\widehat {MPN} = \widehat {ONM} + \widehat {ONP} = {54^o} + {54^o} = {108^o}\).
Xét \(\Delta \) OMN và \(\Delta \) ONP có:
\(\widehat {MON} = \widehat {NOP}\);
OM = OP;
ON chung.
Suy ra \(\Delta \) OMN = \(\Delta \) ONP (c – g – c).
Do đó, MN = NP (hai cạnh tương ứng).
Chứng minh tương tự ta thu được ngũ giác MNPQR có các cạnh bằng nhau và các góc đều bằng nhau ( = 108o).
Vậy MNPQR là một đa giác đều.
Video hướng dẫn giải
Trả lời câu hỏi Vận dụng 1 trang 77 SGK Toán 9 Chân trời sáng tạo
Cho lục giác đều ABCDEF có M, N, P, Q, R, S lần lượt là trung điểm của các cạnh AB, BC, DE, EF, FA. Đa giác MNPQRS có là đa giác đều không? Vì sao?
Phương pháp giải:
- Đọc kĩ dữ kiện đề bài để vẽ hình
- Dựa vào: Đa giác lồi có các cạnh bằng nhau và các góc bằng nhau gọi là đa giác đều.
Lời giải chi tiết:
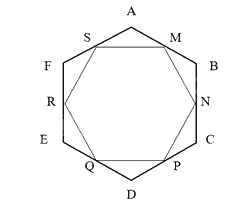
Do ABCDEF là lục giác đều nên:
\(\widehat A = \widehat B = \widehat C = \widehat D = \widehat E = \widehat F = {120^o}\).
- AB = BC = CD = DE = EF = FA.
Vì M, N, P, Q, R, S lần lượt là trung điểm của các cạnh AB, BC, DE, EF, FA.
Suy ra AM = MB = BN = NC = CP = PD = DQ = QE = ER = RF = FS = SA.
Xét \(\Delta \) SAM và \(\Delta \) MBN có:
\(\widehat A = \widehat B\) (chứng minh trên);
AM = BN (chứng minh trên);
SA = MB (chứng minh trên).
Suy ra \(\Delta \) SAM = \(\Delta \) MBN (c – g – c).
Do đó, SM = MN (hai cạnh tương ứng).
Chứng minh tương tự ta được: MN = NP, NP = PQ, QR = RS, RS = SM (1).
Vì AS = AM (chứng minh trên) suy ra \(\Delta \) ASM cân tại A.
suy ra \(\widehat {ASM} = \widehat {AMS}\) (tính chất tam giác cân)
Nên \(\widehat {ASM} = \widehat {AMS} = \frac{{{{180}^o} - \widehat A}}{2} = {30^o}\) (tổng 3 góc trong của tam giác).
Tương tự ta thu được:
\(\widehat {BMN} = \widehat {BNM} = \frac{{{{180}^o} - \widehat B}}{2} = 30\);
\(\widehat {CNP} = \widehat {CPN} = \frac{{{{180}^o} - \widehat C}}{2} = {30^o}\);
\(\widehat {DPQ} = \widehat {DQP} = \frac{{{{180}^o} - \widehat D}}{2} = {30^o}\);
\(\widehat {EQR} = \widehat {ERQ} = \frac{{{{180}^o} - \widehat E}}{2} = {30^o}\);.
\(\widehat {FRS} = \widehat {FSR} = \frac{{{{180}^o} - \widehat F}}{2} = {30^o}\)
Ta có:
\(\widehat {RSM} = {180^o} - \widehat {FRS} - \widehat {ASM} = {180^o} - {30^o} - {30^o} = {120^o}\)
Tương tự, ta được:
\(\widehat {AMN} = \widehat {MNP} = \widehat {NQP} = \widehat {PQR} = \widehat {QRS} = {120^o}\). (2)
Từ (1) và (2), suy ra MNPQRS là đa giác đều.
Mục 1 của chương trình Toán 9 tập 2 - Chân trời sáng tạo tập trung vào việc ôn tập và hệ thống hóa kiến thức về hàm số bậc hai. Các bài tập trong mục này thường yêu cầu học sinh vận dụng các kiến thức đã học để giải quyết các bài toán thực tế, rèn luyện kỹ năng tư duy logic và khả năng giải quyết vấn đề.
Bài 1 yêu cầu học sinh nhắc lại các kiến thức cơ bản về hàm số bậc hai, bao gồm định nghĩa, dạng tổng quát, đồ thị, các tính chất và ứng dụng của hàm số bậc hai. Các em cần nắm vững các khái niệm như hệ số a, b, c, đỉnh của parabol, trục đối xứng, giao điểm với trục hoành và trục tung.
Bài 2 tập trung vào việc giải phương trình bậc hai bằng các phương pháp khác nhau, bao gồm phương pháp phân tích thành nhân tử, phương pháp sử dụng công thức nghiệm và phương pháp hoàn thành bình phương. Các em cần hiểu rõ điều kiện để phương trình bậc hai có nghiệm, nghiệm kép và vô nghiệm.
Bài 3 yêu cầu học sinh vận dụng kiến thức về phương trình bậc hai để giải quyết các bài toán thực tế, chẳng hạn như bài toán tìm chiều dài, chiều rộng của một hình chữ nhật, bài toán tính vận tốc, thời gian và quãng đường. Các em cần biết cách lập phương trình bậc hai từ các dữ kiện của bài toán và giải phương trình để tìm ra nghiệm.
Để giúp các em học sinh hiểu rõ hơn về cách giải các bài tập trong mục 1, chúng tôi xin trình bày hướng dẫn giải chi tiết từng bài tập:
Khi giải các bài tập trong mục 1, các em cần lưu ý những điều sau:
Ngoài sách giáo khoa, các em có thể tham khảo thêm các tài liệu sau để học tốt môn Toán 9:
Hy vọng rằng với hướng dẫn giải chi tiết và những lưu ý trên, các em học sinh sẽ tự tin giải quyết các bài tập trong mục 1 trang 75, 76, 77 SGK Toán 9 tập 2 - Chân trời sáng tạo. Chúc các em học tập tốt!
| Bài tập | Nội dung chính | Phương pháp giải |
|---|---|---|
| Bài 1 | Ôn tập về hàm số bậc hai | Ôn tập kiến thức |
| Bài 2 | Giải phương trình bậc hai | Phân tích, công thức nghiệm |
| Bài 3 | Ứng dụng phương trình bậc hai | Lập phương trình, giải phương trình |