Chào mừng bạn đến với bài học về Lý thuyết Xác suất của biến cố trong chương trình Toán 9 Chân trời sáng tạo. Đây là một chủ đề quan trọng, giúp bạn làm quen với những khái niệm cơ bản của lý thuyết xác suất, một công cụ hữu ích trong nhiều lĩnh vực của cuộc sống.
Tại giaitoan.edu.vn, chúng tôi cung cấp kiến thức đầy đủ, dễ hiểu cùng với các bài tập thực hành đa dạng để bạn có thể nắm vững kiến thức này một cách hiệu quả nhất.
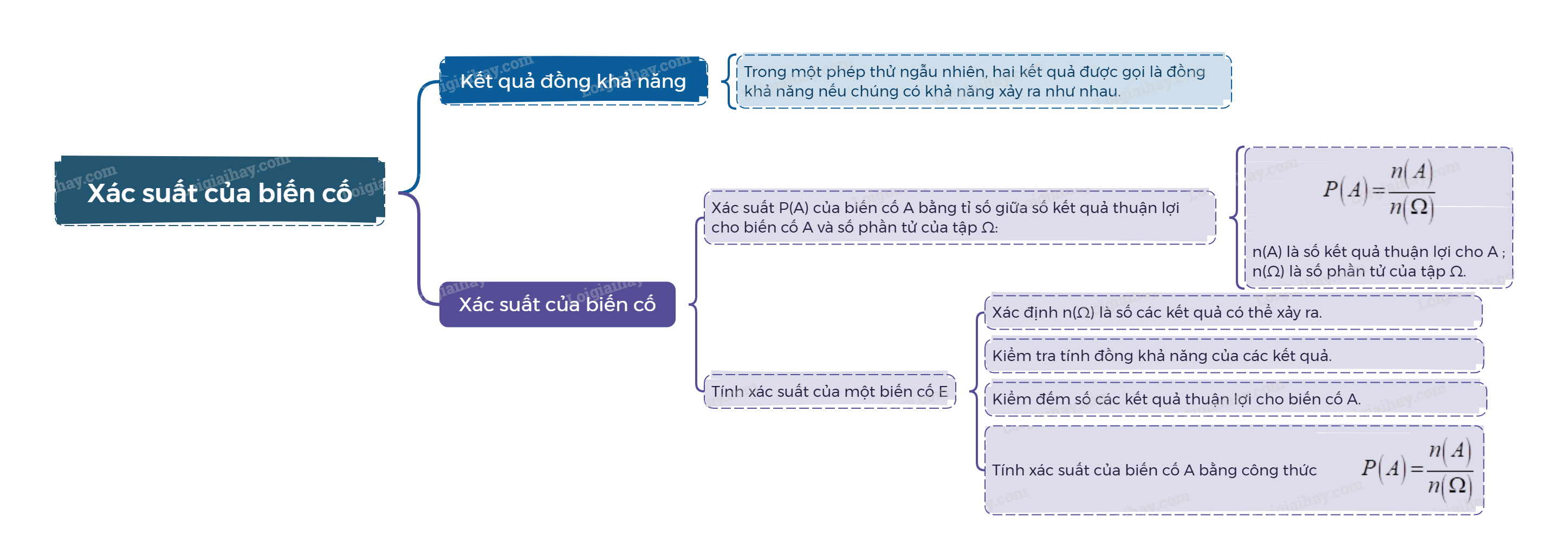
1. Kết quả đồng khả năng Trong một phép thử ngẫu nhiên, hai kết quả được gọi là đồng khả năng nếu chúng có khả năng xảy ra như nhau.
1. Kết quả đồng khả năng
Trong một phép thử ngẫu nhiên, hai kết quả được gọi là đồng khả năng nếu chúng có khả năng xảy ra như nhau. |
Chú ý:
a) Trong phép thử tung đồng xu (hoặc gieo xúc xắc), nếu có giả thiết đồng xu, xúc xắc là cân đối và đồng chất thì các mặt của đồng xu hay xúc xắc sẽ có cùng khả năng xuất hiện.
b) Trong phép thử lấy vật (quả bóng, viên bi,…), nếu có giả thiết các vật có cùng kích thước và khối lượng thì mỗi vật đều có cùng khả năng được lựa chọn.
Ví dụ:

a) Do hai đồng xu cân đối và đồng chất nên các mặt đều có cùng khả năng xuất hiện. Các kết quả của phép thử là đồng khả năng.
b) Do con xúc xắc không cân đối nên khả năng xuất hiện của các mặt không như nhau. Các kết quả của phép thử không đồng khả năng.
2. Xác suất của biến cố
Giả sử một phép thử có không gian mẫu \(\Omega \) gồm hữu hạn các kết quả đồng khả năng và A là một biến cố. Xác suất của biến cố A, kí hiệu là P(A), được xác định bởi công thức \(P\left( A \right) = \frac{{n\left( A \right)}}{{n\left( \Omega \right)}}\), trong đó n(A) là số kết quả thuận lợi cho A và \(n\left( \Omega \right)\) là tổng số các kết quả có thể xảy ra. |
Cách tính xác suất của một biến cố
Bước 1: Xác định n(\(\Omega \)) là số các kết quả có thể xảy ra. Bước 2: Kiểm tra tính đồng khả năng của các kết quả. Bước 3: Kiểm đếm số các kết quả thuận lợi cho biến cố A. Bước 4: Tính xác suất của biến cố A bằng công thức \(P\left( A \right) = \frac{{n\left( A \right)}}{{n\left( \Omega \right)}}\). |
Ví dụ: Ba bạn Bảo, Châu, Dương được xếp ngẫu nhiên ngồi trên một hàng ghế có ba chỗ ngồi. Tính xác suất của các biến cố sau:
a) E: "Bảo không ngồi ngoài cùng bên phải";
b) F: “Châu và Dương không ngồi cạnh nhau”.
Lời giải:
Kí hiệu ba bạn Bảo, Châu, Dương lần lượt là B, C, D.
Ta liệt kê các kết quả có thể xảy ra:
• Bảo ngồi ngoài cùng bên trái: có 2 cách xếp là BCD và BDC.
• Bảo ngồi giữa: có 2 cách xếp là CBD và DBC.
• Bảo ngồi ngoài cùng bên phải: có 2 cách xếp là CDB và DCB.
Vậy không gian mẫu của phép thử là \(\Omega = \left\{ {BCD;{\rm{ }}BDC;{\rm{ }}CBD;{\rm{ }}DBC;{\rm{ }}CDB;{\rm{ }}DCB} \right\}.\)
Tập \(\Omega \) có 6 phần tử.
Vì việc xếp chỗ ngồi là ngẫu nhiên nên các kết quả có thể là đồng khả năng.
a) Có 4 kết quả thuận lợi cho biến cố E là BCD, BDC, CBD và DBC.
Vậy \(P\left( E \right) = \frac{4}{6} = \frac{2}{3}\).
b) Có 2 kết quả thuận lợi cho biến cố F là CBD và DBC.
Vậy \(P\left( F \right) = \frac{2}{6} = \frac{1}{3}\).
Xác suất là một khái niệm toán học dùng để đo lường khả năng xảy ra của một sự kiện ngẫu nhiên. Trong chương trình Toán 9 Chân trời sáng tạo, học sinh sẽ được làm quen với những kiến thức cơ bản về xác suất, bao gồm khái niệm biến cố, xác suất của biến cố, và các quy tắc tính xác suất đơn giản.
Biến cố là một sự kiện mà chúng ta quan tâm đến việc nó có xảy ra hay không trong một thí nghiệm ngẫu nhiên. Ví dụ, khi tung một đồng xu, biến cố “mặt ngửa xuất hiện” là một biến cố.
Xác suất của một biến cố, ký hiệu là P(A), là một số thực nằm trong khoảng từ 0 đến 1, biểu thị khả năng xảy ra của biến cố đó. P(A) = 0 nghĩa là biến cố A không thể xảy ra, P(A) = 1 nghĩa là biến cố A chắc chắn xảy ra.
Xác suất của một biến cố A được tính bằng công thức:
P(A) = (Số các kết quả thuận lợi cho A) / (Tổng số các kết quả có thể xảy ra)
Ví dụ 1: Tung một con xúc xắc 6 mặt. Tính xác suất để mặt 3 chấm xuất hiện.
Ví dụ 2: Rút một lá bài từ một bộ bài 52 lá. Tính xác suất để lá bài đó là lá Át.
Hãy thử giải các bài tập sau để củng cố kiến thức về Lý thuyết Xác suất của biến cố:
Hy vọng rằng bài học này đã giúp bạn hiểu rõ hơn về Lý thuyết Xác suất của biến cố Toán 9 Chân trời sáng tạo. Chúc bạn học tập tốt!