Chào mừng các em học sinh đến với chuyên mục giải bài tập Toán 9 tập 2 của giaitoan.edu.vn. Chúng tôi cung cấp lời giải chi tiết, dễ hiểu cho từng bài tập trong SGK Toán 9 tập 2, giúp các em nắm vững kiến thức và tự tin hơn trong học tập.
Ở bài viết này, chúng ta sẽ cùng nhau giải quyết các bài tập trong mục 2 trang 40, 41, 42 của sách Toán 9 tập 2 - Chân trời sáng tạo. Các em hãy chuẩn bị sách giáo khoa và cùng chúng tôi bắt đầu nhé!
Bác Quảng ghi lại thời gian truy cập Internet của mình mỗi ngày (đơn vị: giờ) trong vòng 1 tháng như sau: Bác Quảng đánh giá mức độ sử dụng Internet mỗi ngày của mình theo bảng tiêu chí sau: Hãy xác định tỉ lệ các ngày trong tháng bác Quảng truy cập Internet ở mức độ “Rất nhiều”.
Video hướng dẫn giải
Trả lời câu hỏi Vận dụng 1 trang 42 SGK Toán 9 Chân trời sáng tạo
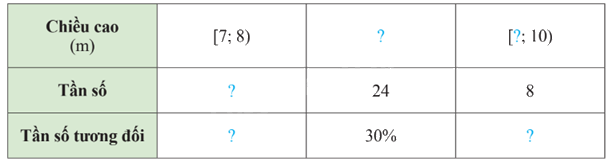
Bác Minh thống kê chiều cao của một số cây bạch đàn 5 năm tuổi ở một lâm trường vào bảng dưới đây (đơn vị: mét). Do sơ suất nên bác Minh ghi thiếu một số số liệu. Hãy giúp bác Minh hoàn thảnh bảng thống kê.
Phương pháp giải:
Tần số tương đối của một nhóm được tính theo công thức \(f = \frac{m}{N}.100\% \) trong đó m là tần số của nhóm và N là cỡ mẫu để tìm các số liệu còn lại
Lời giải chi tiết:
Ta thấy nhóm [7;8) có khoảng cách là 1 nên nhóm thứ hai là [8;9), nhóm thứ 3 là [9;10)
Vì tần số của nhóm [8;9) là 24, ứng với tần số tương đối là 30% nên \(\frac{24}{N}.100\% = 30\%\)
Suy ra \(\frac{24}{N} = 0,3\) nên \(N = \frac{24}{0,3} = 80\)
Do đó tổng tần số là 80.
Khi đó tần số của nhóm [7;8) là: 80 - 24 - 8 = 48
Tần số tương đối của nhóm [7;8) là: \(f = \frac{48}{80}.100\% = 60\%\)
Tần số tương đối của nhóm [9;10) là: \(f = \frac{8}{80}.100\% = 10\%\)
Ta được bảng sau:

Video hướng dẫn giải
Trả lời câu hỏi Thực hành 2 trang 41 SGK Toán 9 Chân trời sáng tạo
Cô Loan ghi lại chiều cao (đơn vị: cm) của các cây bạch đàn giống vừa được chuyển đến nông trường ở bảng sau:
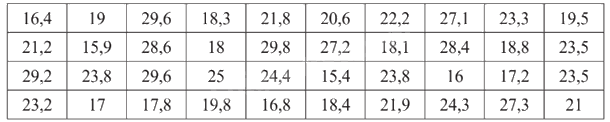
Hãy chia dữ liệu trên thành 5 nhóm, với nhóm đầu tiên gồm các cây có chiều cao từ 15 cm đến dưới 18 cm và lập bảng tần số tương đối ghép nhóm tương ứng.
Phương pháp giải:
- Lập bảng tần số rồi suy ra bảng tần số tương đối
- Tần số tương đối của một nhóm được tính theo công thức \(f = \frac{m}{N}.100\% \) trong đó m là tần số của nhóm và N là cỡ mẫu.
- Bảng tần số tương đối ghép nhóm gồm hai dòng (hoặc hai cột), dòng (hoặc cột) thứ nhất ghi các nhóm số liệu, dòng (hoặc cột) thứ hai ghi các tần số tương đối tương ứng với mỗi nhóm đó.
Lời giải chi tiết:
Ta được bảng sau:

Video hướng dẫn giải
Trả lời câu hỏi Hoạt động 2 trang 40 SGK Toán 9 Chân trời sáng tạo
Bác Quảng ghi lại thời gian truy cập Internet của mình mỗi ngày (đơn vị: giờ) trong vòng 1 tháng như sau:

Bác Quảng đánh giá mức độ sử dụng Internet mỗi ngày của mình theo bảng tiêu chí sau:

Hãy xác định tỉ lệ các ngày trong tháng bác Quảng truy cập Internet ở mức độ “Rất nhiều”.
Phương pháp giải:
- Dựa vào: Số lượng các giá trị của mẫu số liệu thuộc vào một nhóm được gọi là tần số của nhóm.
- Bảng tần số ghép nhóm biểu diễn tần số của các nhóm số liệu. Bảng gồm hai dòng (hoặc hai cột), dòng (hoặc cột) thứ nhất ghi nhóm số liệu, dòng (hoặc cột) thứ hai ghi các tần số tương ứng với mỗi nhóm đó.
Lời giải chi tiết:
Bảng tần số ghép nhóm của mẫu dữ liệu:

Vậy tỉ lệ các ngày trong tháng bác Quảng truy cập Internet ở mức độ “Rất nhiều” là: \(\frac{4}{{30}}.100\% = 13,3\% \).
Video hướng dẫn giải
Trả lời câu hỏi Hoạt động 2 trang 40 SGK Toán 9 Chân trời sáng tạo
Bác Quảng ghi lại thời gian truy cập Internet của mình mỗi ngày (đơn vị: giờ) trong vòng 1 tháng như sau:

Bác Quảng đánh giá mức độ sử dụng Internet mỗi ngày của mình theo bảng tiêu chí sau:

Hãy xác định tỉ lệ các ngày trong tháng bác Quảng truy cập Internet ở mức độ “Rất nhiều”.
Phương pháp giải:
- Dựa vào: Số lượng các giá trị của mẫu số liệu thuộc vào một nhóm được gọi là tần số của nhóm.
- Bảng tần số ghép nhóm biểu diễn tần số của các nhóm số liệu. Bảng gồm hai dòng (hoặc hai cột), dòng (hoặc cột) thứ nhất ghi nhóm số liệu, dòng (hoặc cột) thứ hai ghi các tần số tương ứng với mỗi nhóm đó.
Lời giải chi tiết:
Bảng tần số ghép nhóm của mẫu dữ liệu:

Vậy tỉ lệ các ngày trong tháng bác Quảng truy cập Internet ở mức độ “Rất nhiều” là: \(\frac{4}{{30}}.100\% = 13,3\% \).
Video hướng dẫn giải
Trả lời câu hỏi Thực hành 2 trang 41 SGK Toán 9 Chân trời sáng tạo
Cô Loan ghi lại chiều cao (đơn vị: cm) của các cây bạch đàn giống vừa được chuyển đến nông trường ở bảng sau:
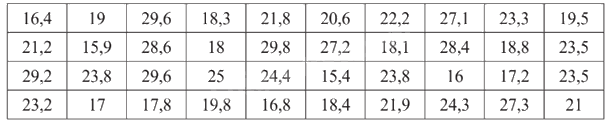
Hãy chia dữ liệu trên thành 5 nhóm, với nhóm đầu tiên gồm các cây có chiều cao từ 15 cm đến dưới 18 cm và lập bảng tần số tương đối ghép nhóm tương ứng.
Phương pháp giải:
- Lập bảng tần số rồi suy ra bảng tần số tương đối
- Tần số tương đối của một nhóm được tính theo công thức \(f = \frac{m}{N}.100\% \) trong đó m là tần số của nhóm và N là cỡ mẫu.
- Bảng tần số tương đối ghép nhóm gồm hai dòng (hoặc hai cột), dòng (hoặc cột) thứ nhất ghi các nhóm số liệu, dòng (hoặc cột) thứ hai ghi các tần số tương đối tương ứng với mỗi nhóm đó.
Lời giải chi tiết:
Ta được bảng sau:

Video hướng dẫn giải
Trả lời câu hỏi Vận dụng 1 trang 42 SGK Toán 9 Chân trời sáng tạo
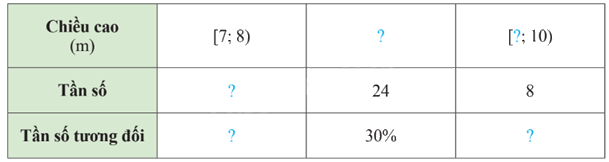
Bác Minh thống kê chiều cao của một số cây bạch đàn 5 năm tuổi ở một lâm trường vào bảng dưới đây (đơn vị: mét). Do sơ suất nên bác Minh ghi thiếu một số số liệu. Hãy giúp bác Minh hoàn thảnh bảng thống kê.
Phương pháp giải:
Tần số tương đối của một nhóm được tính theo công thức \(f = \frac{m}{N}.100\% \) trong đó m là tần số của nhóm và N là cỡ mẫu để tìm các số liệu còn lại
Lời giải chi tiết:
Ta thấy nhóm [7;8) có khoảng cách là 1 nên nhóm thứ hai là [8;9), nhóm thứ 3 là [9;10)
Vì tần số của nhóm [8;9) là 24, ứng với tần số tương đối là 30% nên \(\frac{24}{N}.100\% = 30\%\)
Suy ra \(\frac{24}{N} = 0,3\) nên \(N = \frac{24}{0,3} = 80\)
Do đó tổng tần số là 80.
Khi đó tần số của nhóm [7;8) là: 80 - 24 - 8 = 48
Tần số tương đối của nhóm [7;8) là: \(f = \frac{48}{80}.100\% = 60\%\)
Tần số tương đối của nhóm [9;10) là: \(f = \frac{8}{80}.100\% = 10\%\)
Ta được bảng sau:

Mục 2 của chương trình Toán 9 tập 2 - Chân trời sáng tạo tập trung vào việc ôn tập và củng cố kiến thức về hàm số bậc hai. Các bài tập trong mục này yêu cầu học sinh vận dụng các kiến thức đã học để giải quyết các bài toán thực tế, đồng thời rèn luyện kỹ năng tư duy logic và khả năng giải quyết vấn đề.
Bài tập này yêu cầu học sinh xác định các hệ số a, b, c của hàm số bậc hai có dạng y = ax2 + bx + c. Để làm được bài này, học sinh cần nắm vững định nghĩa của hàm số bậc hai và biết cách nhận biết các hệ số a, b, c.
Tập xác định của hàm số bậc hai là tập hợp tất cả các giá trị của x sao cho hàm số có nghĩa. Trong hầu hết các trường hợp, tập xác định của hàm số bậc hai là tập số thực R. Tuy nhiên, có một số trường hợp đặc biệt, ví dụ như khi hàm số có mẫu số chứa biến x, thì tập xác định sẽ bị giới hạn bởi các giá trị của x làm cho mẫu số bằng 0.
Để vẽ đồ thị của hàm số bậc hai, học sinh cần thực hiện các bước sau:
Giá trị lớn nhất hoặc nhỏ nhất của hàm số bậc hai đạt được tại đỉnh của parabol. Nếu a > 0 thì parabol có dạng chữ U, và giá trị nhỏ nhất của hàm số là tung độ của đỉnh. Nếu a < 0 thì parabol có dạng chữ ∩, và giá trị lớn nhất của hàm số là tung độ của đỉnh.
Để giải các bài tập trong mục 2 trang 40, 41, 42 SGK Toán 9 tập 2 - Chân trời sáng tạo một cách hiệu quả, học sinh cần:
Ví dụ: Cho hàm số y = 2x2 - 4x + 1. Hãy xác định hệ số a, b, c và tìm tọa độ đỉnh của parabol.
Giải:
Hy vọng rằng với những hướng dẫn chi tiết và ví dụ minh họa trên, các em học sinh đã có thể tự tin giải quyết các bài tập trong mục 2 trang 40, 41, 42 SGK Toán 9 tập 2 - Chân trời sáng tạo. Chúc các em học tập tốt và đạt kết quả cao trong môn Toán!