Chào mừng bạn đến với bài học lý thuyết về phương trình bậc nhất hai ẩn và hệ hai phương trình bậc nhất hai ẩn trong chương trình Toán 9 Chân trời sáng tạo. Đây là một phần kiến thức quan trọng, nền tảng cho các bài toán phức tạp hơn ở các lớp trên.
Bài học này sẽ cung cấp cho bạn những kiến thức cơ bản nhất về định nghĩa, cách giải và ứng dụng của phương trình bậc nhất hai ẩn và hệ phương trình này. Chúng tôi sẽ trình bày một cách dễ hiểu, kèm theo nhiều ví dụ minh họa để bạn có thể nắm bắt kiến thức một cách nhanh chóng và hiệu quả.
1. Phương trình bậc nhất hai ẩn Khái niệm phương trình bậc nhất hai ẩn Phương trình bậc nhất hai ẩn x và y là hệ thức dạng (ax + by = c), trong đó a, b và c là các số đã biết (gọi là hệ số), (a ne 0) hoặc (b ne 0).
1. Phương trình bậc nhất hai ẩn
Khái niệm phương trình bậc nhất hai ẩn
Phương trình bậc nhất hai ẩn x và y là hệ thức dạng \(ax + by = c\), trong đó a, b và c là các số đã biết (gọi là hệ số), \(a \ne 0\) hoặc \(b \ne 0\). |
Ví dụ: \(2x + 3y = 4\), \(0x + 2y = 3\), \(x + 0y = 2\) là các phương trình bậc nhất hai ẩn.
Nghiệm của phương trình bậc nhất hai ẩn
Nếu giá trị của vế trái tại \(x = {x_0}\) và \(y = {y_0}\) bằng vế phải thì cặp số \(\left( {{x_0};{y_0}} \right)\) được gọi là một nghiệm của phương trình. Giải phương trình là tìm tất cả các nghiệm của phương trình đó. |
Ví dụ: Cặp số \(( - 1;2)\) là nghiệm của phương trình \(2x + 3y = 4\) vì \(2.\left( { - 1} \right) + 3.2 = - 2 + 6 = 4\).
Cặp số \((1;2)\) không là nghiệm của phương trình \(2x + 3y = 4\) vì
\(2.1 + 3.2 = 2 + 6 = 8 \ne 4\).
Biểu diễn nghiệm trên mặt phẳng tọa độ Oxy
- Mỗi nghiệm \(\left( {{x_0};{y_0}} \right)\) của phương trình \(ax + by = c\) được biểu diễn bởi điểm có tọa độ \(\left( {{x_0};{y_0}} \right)\) trên mặt phẳng tọa độ.
- Phương trình bậc nhất hai ẩn \(ax + by = c\) luôn luôn có vô số nghiệm. Tất cả các nghiệm của phương trình đó được biểu diễn bởi một đường thẳng.
Ví dụ:
Nghiệm của phương trình \( - 3x + y = 2\) được biểu diễn bởi đường thẳng d: \(y = 3x + 2\).
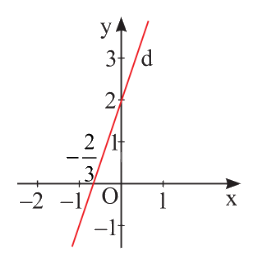
Nghiệm của phương trình \(0x + y = - 2\) được biểu diễn bởi đường thẳng d: \(y = - 2\) vuông góc với Oy tại điểm \(M\left( {0; - 2} \right)\).
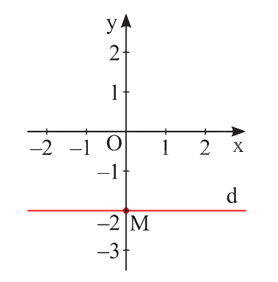
Nghiệm của phương trình \(2x + 0y = 3\) được biểu diễn bởi đường thẳng d: \(x = 1,5\) vuông góc với Ox tại điểm \(N\left( {1,5;0} \right)\).
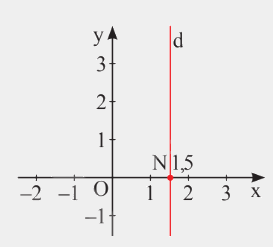
2. Hệ hai phương trình bậc nhất hai ẩn
Khái niệm hệ hai phương trình bậc nhất hai ẩn
Hệ hai phương trình bậc nhất hai ẩn x, y có dạng: \(\left\{ \begin{array}{l}ax + by = c\,\,\,\,\,\,\,\,\,(1)\\a'x + b'y = c'\,\,(2)\end{array} \right.\,\,\,\) Trong đó a, b, c, a’, b’, c’ là các số đã biết (gọi là hệ số), \(a \ne 0\) hoặc \(b \ne 0\), \(a' \ne 0\) hoặc \(b' \ne 0\). |
Ví dụ: Hệ phương trình \(\left\{ \begin{array}{l}2x - y = 0\\x + y = 3\end{array} \right.\), \(\left\{ \begin{array}{l}3x = 1\\x - y = 3\end{array} \right.\), \(\left\{ \begin{array}{l}4x - y = 3\\3y = 6\end{array} \right.\) là các hệ phương trình bậc nhất hai ẩn.
Nghiệm của hệ hai phương trình bậc nhất hai ẩn
Nếu \(\left( {{x_0};{y_0}} \right)\) là nghiệm chung của hai phương trình (1) và (2) thì \(\left( {{x_0};{y_0}} \right)\) được gọi là một nghiệm của hệ. Giải hệ phương trình là tìm tất cả các nghiệm của hệ phương trình đó. |
Ví dụ: Cặp số (1; 2) là một nghiệm của hệ phương trình \(\left\{ \begin{array}{l}2x - y = 0\\x + y = 3\end{array} \right.\), vì:
\(2x - y = 2.1 - 2 = 0\) nên (1; 2) là nghiệm của phương trình thứ nhất.
\(x + y = 1 + 2 = 3\) nên (1; 2) là nghiệm của phương trình thứ hai.
Phương trình bậc nhất hai ẩn là phương trình có dạng tổng quát ax + by = c, trong đó a, b, c là các số thực và a, b không đồng thời bằng 0. x và y là các ẩn số của phương trình.
Để hiểu rõ hơn, ta xét một số ví dụ:
Nghiệm của phương trình bậc nhất hai ẩn là cặp số (x0; y0) thỏa mãn phương trình, tức là ax0 + by0 = c.
Trên mặt phẳng tọa độ Oxy, phương trình bậc nhất hai ẩn ax + by = c biểu diễn bằng một đường thẳng.
Hệ hai phương trình bậc nhất hai ẩn có dạng:
{ ax + by = c a'x + b'y = c' }
Trong đó a, b, a', b', c, c' là các số thực và a, b, a', b' không đồng thời bằng 0.
Có hai phương pháp phổ biến để giải hệ hai phương trình bậc nhất hai ẩn:
Ví dụ 1: Giải hệ phương trình sau bằng phương pháp thế:
{ x + y = 5 2x - y = 1 }
Giải:
Từ phương trình x + y = 5, ta có y = 5 - x. Thay vào phương trình 2x - y = 1, ta được:
2x - (5 - x) = 1 ⇔ 2x - 5 + x = 1 ⇔ 3x = 6 ⇔ x = 2
Thay x = 2 vào y = 5 - x, ta được y = 5 - 2 = 3
Vậy nghiệm của hệ phương trình là (x; y) = (2; 3).
Ví dụ 2: Giải hệ phương trình sau bằng phương pháp cộng đại số:
{ 3x + 2y = 7 x - 2y = 1 }
Giải:
Cộng hai phương trình, ta được:
(3x + 2y) + (x - 2y) = 7 + 1 ⇔ 4x = 8 ⇔ x = 2
Thay x = 2 vào phương trình x - 2y = 1, ta được:
2 - 2y = 1 ⇔ 2y = 1 ⇔ y = 1/2
Vậy nghiệm của hệ phương trình là (x; y) = (2; 1/2).
Phương trình bậc nhất hai ẩn và hệ hai phương trình bậc nhất hai ẩn được ứng dụng rộng rãi trong nhiều lĩnh vực của đời sống và khoa học, như:
Hy vọng bài học này đã giúp bạn hiểu rõ hơn về lý thuyết phương trình bậc nhất hai ẩn và hệ hai phương trình bậc nhất hai ẩn Toán 9 Chân trời sáng tạo. Chúc bạn học tập tốt!