Chào mừng bạn đến với giaitoan.edu.vn, nơi cung cấp lời giải chi tiết và dễ hiểu cho các bài tập Toán 9. Bài viết này sẽ hướng dẫn bạn giải quyết hoàn toàn mục 2 trang 63 SGK Toán 9 tập 1 - Chân trời sáng tạo, giúp bạn nắm vững kiến thức và tự tin hơn trong quá trình học tập.
Chúng tôi luôn cố gắng cung cấp nội dung chính xác, đầy đủ và dễ tiếp cận, hỗ trợ tối đa cho học sinh trong việc học Toán.
a) Tính các tỉ số lượng giác của góc (alpha ) và của góc 90o -(alpha ) trong Hình 8 theo a, b, c. b) So sánh sin (widehat B) và cos (widehat C) , cos (widehat B) và sin (widehat C) , tan (widehat B) và cot (widehat C) , tan (widehat C) và cot (widehat B).
Video hướng dẫn giải
Trả lời câu hỏi Thực hành 3 trang 63SGK Toán 9 Chân trời sáng tạo
a) So sánh: sin 72o và cos 18o ; cos 72o và sin 18o; tan 72o và cot 18o
b) Cho biết sin 18o \( \approx 0,31\) ; tan 18o \( \approx 0,32\). Tính cos 72o và cot 72o.
Phương pháp giải:
- Dựa vào nếu hai góc phụ nhau thì sin góc này bằng cos góc kia, tan góc này bằng cot góc kia.
- Dựa vào VD3 trang 63 làm tương tự.
Lời giải chi tiết:
a) sin 72o = cos (90 o – 72o)= cos 18o
cos 72o = sin(90 o – 72o)= sin 18o
tan 72o = cot(90 o – 72o)= cot 18o
b) Theo đề bài ta có: sin 18o \( \approx 0,31\) ; tan 18o \( \approx 0,32\).
Suy ra cos 72o = sin(90 o – 72o)= sin 18o \( \approx 0,31\)
và cot 72o = tan(90 o – 72o)= tan 18o \( \approx 0,32\).
Video hướng dẫn giải
Trả lời câu hỏi Hoạt động 3 trang 63 SGK Toán 9 Chân trời sáng tạo
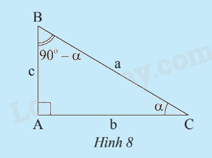
a) Tính các tỉ số lượng giác của góc \(\alpha \) và của góc 90o -\(\alpha \) trong Hình 8 theo a, b, c.
b) So sánh sin \(\widehat B\) và cos \(\widehat C\) , cos \(\widehat B\) và sin \(\widehat C\) , tan \(\widehat B\) và cot \(\widehat C\) , tan \(\widehat C\) và cot \(\widehat B\).
Phương pháp giải:
- Dựa vào tỉ số lượng giác của góc nhọn \(\alpha \). Xét tam giác ABC vuông tại A có \(\widehat {ACB} = \alpha \) , ta có:
+ Tỉ số giữa cạnh đối và cạnh huyền được gọi là sin của góc \(\alpha \) , kí hiệu sin\(\alpha \).
+ Tỉ số giữa cạnh kề và cạnh huyền được gọi là côsin của góc \(\alpha \) , kí hiệu cos\(\alpha \).
+ Tỉ số giữa cạnh đối và cạnh kề được gọi là tang của góc \(\alpha \) , kí hiệu tan\(\alpha \).
+ Tỉ số giữa cạnh kề và cạnh đối được gọi là côtang của góc \(\alpha \) , kí hiệu cot\(\alpha \).
Lời giải chi tiết:
Xét tam giác ABC vuông tại A. Ta có:
Các tỉ số lượng giác của góc \(\alpha \) là:
sin \(\alpha \) = \(\frac{{AB}}{{BC}} = \frac{c}{a}\)
cos \(\alpha \) = \(\frac{{AC}}{{BC}} = \frac{b}{a}\)
tan \(\alpha \) = \(\frac{{AB}}{{AC}} = \frac{c}{b}\)
cot \(\alpha \) = \(\frac{1}{{\tan \alpha }} = \frac{b}{c}\)
Các tỉ số lượng giác của góc 90o - \(\alpha \) là:
sin 90o - \(\alpha \) = \(\frac{{AC}}{{BC}} = \frac{b}{a}\)
cos 90o - \(\alpha \) = \(\frac{{AB}}{{BC}} = \frac{c}{a}\)
tan 90o - \(\alpha \) = \(\frac{{AC}}{{AB}} = \frac{b}{c}\)
cot 90o - \(\alpha \) = \(\frac{1}{{\tan {{90}^o} - \alpha }} = \frac{c}{b}\)
b) Ta có \(\widehat C\) = \(\alpha \) ; \(\widehat B\) = 90o - \(\alpha \) nên theo phần a ta có:
sin \(\widehat B\) = cos \(\widehat C\)
cos \(\widehat B\) = sin \(\widehat C\)
tan \(\widehat B\) = cot \(\widehat C\)
tan \(\widehat C\) = cot \(\widehat B\)
Video hướng dẫn giải
Trả lời câu hỏi Vận dụng3 trang 63 SGK Toán 9 Chân trời sáng tạo
Tia nắng chiếu qua điểm B của nóc tòa nhà tạo với mặt đất một góc x và tạo với cạnh AB của tòa nhà một góc y (Hình 9). Cho biết cos x \( \approx 0,78\) và cot x \( \approx 1,25\). Tính sin y và tan y (kết quả làm tròn đến hàng phần trăm).
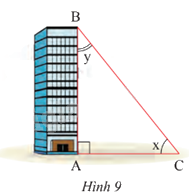
Phương pháp giải:
Dựa vào nếu hai góc phụ nhau thì sin góc này bằng cos góc kia, tan góc này bằng cot góc kia.
Lời giải chi tiết:
Xét tam giác ABC vuông tại A, áp dụng tỉ số lượng giác hai góc phụ nhau, ta có:
sin y = cos x \( \approx 0,78\) ; tan y = cot x \( \approx 1,25\).
Video hướng dẫn giải
Trả lời câu hỏi Hoạt động 3 trang 63 SGK Toán 9 Chân trời sáng tạo
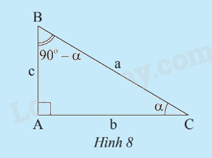
a) Tính các tỉ số lượng giác của góc \(\alpha \) và của góc 90o -\(\alpha \) trong Hình 8 theo a, b, c.
b) So sánh sin \(\widehat B\) và cos \(\widehat C\) , cos \(\widehat B\) và sin \(\widehat C\) , tan \(\widehat B\) và cot \(\widehat C\) , tan \(\widehat C\) và cot \(\widehat B\).
Phương pháp giải:
- Dựa vào tỉ số lượng giác của góc nhọn \(\alpha \). Xét tam giác ABC vuông tại A có \(\widehat {ACB} = \alpha \) , ta có:
+ Tỉ số giữa cạnh đối và cạnh huyền được gọi là sin của góc \(\alpha \) , kí hiệu sin\(\alpha \).
+ Tỉ số giữa cạnh kề và cạnh huyền được gọi là côsin của góc \(\alpha \) , kí hiệu cos\(\alpha \).
+ Tỉ số giữa cạnh đối và cạnh kề được gọi là tang của góc \(\alpha \) , kí hiệu tan\(\alpha \).
+ Tỉ số giữa cạnh kề và cạnh đối được gọi là côtang của góc \(\alpha \) , kí hiệu cot\(\alpha \).
Lời giải chi tiết:
Xét tam giác ABC vuông tại A. Ta có:
Các tỉ số lượng giác của góc \(\alpha \) là:
sin \(\alpha \) = \(\frac{{AB}}{{BC}} = \frac{c}{a}\)
cos \(\alpha \) = \(\frac{{AC}}{{BC}} = \frac{b}{a}\)
tan \(\alpha \) = \(\frac{{AB}}{{AC}} = \frac{c}{b}\)
cot \(\alpha \) = \(\frac{1}{{\tan \alpha }} = \frac{b}{c}\)
Các tỉ số lượng giác của góc 90o - \(\alpha \) là:
sin 90o - \(\alpha \) = \(\frac{{AC}}{{BC}} = \frac{b}{a}\)
cos 90o - \(\alpha \) = \(\frac{{AB}}{{BC}} = \frac{c}{a}\)
tan 90o - \(\alpha \) = \(\frac{{AC}}{{AB}} = \frac{b}{c}\)
cot 90o - \(\alpha \) = \(\frac{1}{{\tan {{90}^o} - \alpha }} = \frac{c}{b}\)
b) Ta có \(\widehat C\) = \(\alpha \) ; \(\widehat B\) = 90o - \(\alpha \) nên theo phần a ta có:
sin \(\widehat B\) = cos \(\widehat C\)
cos \(\widehat B\) = sin \(\widehat C\)
tan \(\widehat B\) = cot \(\widehat C\)
tan \(\widehat C\) = cot \(\widehat B\)
Video hướng dẫn giải
Trả lời câu hỏi Thực hành 3 trang 63SGK Toán 9 Chân trời sáng tạo
a) So sánh: sin 72o và cos 18o ; cos 72o và sin 18o; tan 72o và cot 18o
b) Cho biết sin 18o \( \approx 0,31\) ; tan 18o \( \approx 0,32\). Tính cos 72o và cot 72o.
Phương pháp giải:
- Dựa vào nếu hai góc phụ nhau thì sin góc này bằng cos góc kia, tan góc này bằng cot góc kia.
- Dựa vào VD3 trang 63 làm tương tự.
Lời giải chi tiết:
a) sin 72o = cos (90 o – 72o)= cos 18o
cos 72o = sin(90 o – 72o)= sin 18o
tan 72o = cot(90 o – 72o)= cot 18o
b) Theo đề bài ta có: sin 18o \( \approx 0,31\) ; tan 18o \( \approx 0,32\).
Suy ra cos 72o = sin(90 o – 72o)= sin 18o \( \approx 0,31\)
và cot 72o = tan(90 o – 72o)= tan 18o \( \approx 0,32\).
Video hướng dẫn giải
Trả lời câu hỏi Vận dụng3 trang 63 SGK Toán 9 Chân trời sáng tạo
Tia nắng chiếu qua điểm B của nóc tòa nhà tạo với mặt đất một góc x và tạo với cạnh AB của tòa nhà một góc y (Hình 9). Cho biết cos x \( \approx 0,78\) và cot x \( \approx 1,25\). Tính sin y và tan y (kết quả làm tròn đến hàng phần trăm).
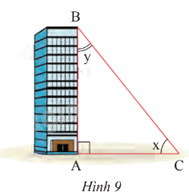
Phương pháp giải:
Dựa vào nếu hai góc phụ nhau thì sin góc này bằng cos góc kia, tan góc này bằng cot góc kia.
Lời giải chi tiết:
Xét tam giác ABC vuông tại A, áp dụng tỉ số lượng giác hai góc phụ nhau, ta có:
sin y = cos x \( \approx 0,78\) ; tan y = cot x \( \approx 1,25\).
Mục 2 trang 63 SGK Toán 9 tập 1 - Chân trời sáng tạo thường xoay quanh các chủ đề về hàm số bậc nhất, bao gồm việc xác định hàm số, vẽ đồ thị hàm số, và ứng dụng của hàm số trong giải quyết các bài toán thực tế. Việc nắm vững kiến thức về hàm số bậc nhất là nền tảng quan trọng cho các chương trình học Toán ở các lớp trên.
Để giải quyết mục 2 trang 63, học sinh cần hiểu rõ các khái niệm sau:
Các bài tập trong mục 2 thường yêu cầu học sinh:
Để giải các bài tập trong mục 2 trang 63, bạn có thể áp dụng các bước sau:
Bài tập: Cho hàm số y = 2x - 1. Hãy vẽ đồ thị hàm số và tìm tọa độ giao điểm của đồ thị với trục hoành.
Giải:
Khi giải các bài tập về hàm số bậc nhất, bạn cần lưu ý:
Để học tập và ôn luyện kiến thức về hàm số bậc nhất, bạn có thể tham khảo các tài liệu sau:
Hy vọng rằng bài viết này đã cung cấp cho bạn những kiến thức và kỹ năng cần thiết để giải quyết mục 2 trang 63 SGK Toán 9 tập 1 - Chân trời sáng tạo một cách hiệu quả. Chúc bạn học tập tốt!