Bài tập 5 trang 89 SGK Toán 9 tập 1 thuộc chương Hàm số bậc nhất. Bài tập này yêu cầu học sinh vận dụng kiến thức về hàm số bậc nhất để giải quyết các bài toán thực tế. Giaitoan.edu.vn xin giới thiệu lời giải chi tiết, dễ hiểu, giúp các em học sinh nắm vững kiến thức và làm bài tập hiệu quả.
Chúng tôi luôn cập nhật nhanh chóng và chính xác các lời giải bài tập Toán 9 tập 1 - Chân trời sáng tạo.
Cho đường tròn (O; R) có đường kính AB. Vẽ dây AC sao cho AC = R. Gọi I là trung điểm dây AC. Đường thẳng OI cắt tiếp tuyến Ax tại M. Chứng minh rằng: a) (widehat {ACB}) có số đo bằng 90o, từ đó suy ra độ dài của BC theo R; b) OM là tia phân giác của (widehat {COA}). c) MC là tiếp tuyến của đường tròn (O; R).
Đề bài
Cho đường tròn (O; R) có đường kính AB. Vẽ dây AC sao cho AC = R. Gọi I là trung điểm dây AC. Đường thẳng OI cắt tiếp tuyến Ax tại M. Chứng minh rằng:
a) \(\widehat {ACB}\) có số đo bằng 90o, từ đó suy ra độ dài của BC theo R;
b) OM là tia phân giác của \(\widehat {COA}\).
c) MC là tiếp tuyến của đường tròn (O; R).
Video hướng dẫn giải
Phương pháp giải - Xem chi tiết
- Dựa vào dữ kiện đề bài để vẽ hình.
- Tính BC theo R bằng cách áp dụng định lý Pythagore trong tam giác vuông ABC.
- Chứng minh OI \( \bot \) AC, tam giác OAC là tam giác cân suy ra OI vừa là trung tuyến và vừa phân giác \(\widehat {COA}\) nên OM là tia phân giác của \(\widehat {COA}\).
- Chứng minh tam giác AOM = tam giác OCM suy ra \(\widehat {OAM} = \widehat {OCM} = {90^o}\). Do đó, MC là tiếp tuyến của đường tròn (O; R).
Lời giải chi tiết
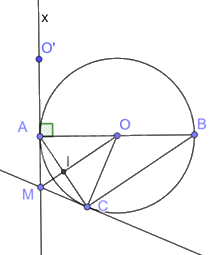
a) Theo giả thiết ta có \(\widehat {ACB} = {90^o}\)
Áp dụng định lý Pythagore tam giác ABC vuông tại C, ta có:
AB2 = AC2 + BC2 .Do đó BC2 = AB2 - AC2 = (2R)2 – R2 = 3R2
Mà BC > 0 nên BC = \(R\sqrt 3 \).
b) Ta có IA = IC và AC là dây cung.
Suy ra OI \( \bot \) AC tại I (Trong một đường tròn, đường kính vuông góc với dây thì đi qua trung điểm của dây đó).
Trong tam giác OAC có OA = OC (= R)
Suy ra tam giác OAC là tam giác cân tại O.
Mà OI là đường trung tuyến của tam giác OAC.
Nên OI cũng là đường phân giác của góc COA
Vậy OM là phân giác \(\widehat {COA}\).
c) Xét \(\Delta \)OAM và \(\Delta \)OCM, ta có:
OA = OC = R
\(\widehat {AOM} = \widehat {COM}\) (Vì OM là phân giác góc AOC)
Cạnh chung OM
Suy ra \(\Delta \)OAM = \(\Delta \)OCM (c.g.c)
Nên \(\widehat {OAM} = \widehat {OCM}\) mà \(\widehat {OAM} = {90^o}\)(AM là tiếp tuyến tại A của (O; R))
Nên \(\widehat {OCM} = {90^o}\).
Do đó: \(MC \bot OC\) tại C.
Vậy MC là tiếp tuyến của đường tròn (O; R).
Bài tập 5 trang 89 SGK Toán 9 tập 1 - Chân trời sáng tạo là một bài tập quan trọng trong chương Hàm số bậc nhất. Bài tập này giúp học sinh củng cố kiến thức về hàm số bậc nhất, cách xác định hàm số, và cách giải các bài toán liên quan đến hàm số.
(Nội dung đề bài sẽ được chèn vào đây - ví dụ: Cho hàm số y = 2x + 3. Hãy tìm x khi y = 7.)
Để giải bài tập này, chúng ta cần hiểu rõ các khái niệm cơ bản về hàm số bậc nhất:
Ví dụ minh họa:
(Giải chi tiết bài tập 5 với các bước rõ ràng, sử dụng công thức và giải thích cụ thể.)
Ngoài bài tập 5, chương Hàm số bậc nhất còn có nhiều bài tập tương tự. Dưới đây là một số dạng bài tập thường gặp:
Để giải bài tập Hàm số bậc nhất hiệu quả, bạn có thể áp dụng một số mẹo sau:
Để hiểu rõ hơn về Hàm số bậc nhất, bạn có thể tham khảo thêm các tài liệu sau:
Bài tập 5 trang 89 SGK Toán 9 tập 1 - Chân trời sáng tạo là một bài tập quan trọng giúp học sinh củng cố kiến thức về hàm số bậc nhất. Hy vọng với lời giải chi tiết và các mẹo giải bài tập hiệu quả mà Giaitoan.edu.vn cung cấp, các em học sinh sẽ tự tin hơn khi làm bài tập và đạt kết quả tốt trong môn Toán.
| Khái niệm | Giải thích |
|---|---|
| Hàm số bậc nhất | y = ax + b (a ≠ 0) |
| Hệ số a | Xác định độ dốc của đường thẳng |
| Hệ số b | Xác định giao điểm của đường thẳng với trục tung |
| Bảng tóm tắt các khái niệm quan trọng | |