Chào mừng bạn đến với giaitoan.edu.vn, nơi cung cấp lời giải chi tiết và dễ hiểu cho các bài tập Toán 9. Bài viết này sẽ hướng dẫn bạn giải quyết mục 2 trang 90 SGK Toán 9 tập 2 - Chân trời sáng tạo một cách nhanh chóng và hiệu quả.
Chúng tôi hiểu rằng việc học Toán đôi khi có thể gặp nhiều khó khăn. Vì vậy, chúng tôi luôn cố gắng cung cấp những giải pháp tốt nhất để giúp bạn nắm vững kiến thức và đạt kết quả cao trong học tập.
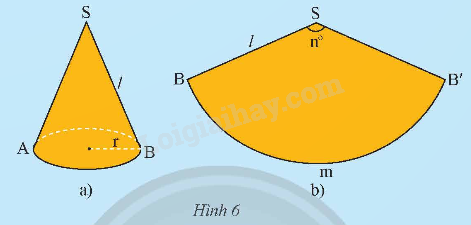
Cho một hình nón có bán kính r, có độ dài đường sinh l (Hình 6a). Cắt mặt xung quanh của hình nón theo một đường sinh của nó rồi trải phẳng ra, ta được hình quạt tròn (Hình 6b). Tính theo r và l: a) Độ dài cung BB’; b) Số đo cung BB’; c) Diện tích của hình quạt tròn.
Video hướng dẫn giải
Trả lời câu hỏi Thực hành 3 trang 90SGK Toán 9 Chân trời sáng tạo
Tính diện tích xung quanh và diện tích toàn phần của hình nón có đường kính đáy d = 10 m và chiều cao h = 12 m (kết quả làm tròn đến hàng phần trăm).
Phương pháp giải:
- Dựa vào diện tích xung quanh của hình nón có bán kính r, độ dài đường sinh l là: \({S_{xq}} = \pi rl\)
- Diện tích toàn phần \({S_{tp}} = {S_{xq}} + {S_{day}}\) để tính.
Lời giải chi tiết:
Bán kính của đáy là: \(r = \frac{d}{2} = \frac{10}{2} = 5 (m)\)
Ta có \(l = \sqrt {{r^2} + {h^2}} = \sqrt {{5^2} + {12^2}} = 13 (m).\)
Diện tích xung quanh là:
\({S_{xq}} = \pi rl = \pi .5.13 = 65 \pi\) (m2)
Diện tích toàn phần là:
\({S_{tp}} = {S_{xq}} + {S_{đáy}} = 65 \pi + \pi {r^2} = 65 \pi + \pi {.5^2} = 90\pi \approx\) 282, 74 m2.
Video hướng dẫn giải
Trả lời câu hỏi Hoạt động 2 trang 90 SGK Toán 9 Chân trời sáng tạo
Cho một hình nón có bán kính r, có độ dài đường sinh l (Hình 6a). Cắt mặt xung quanh của hình nón theo một đường sinh của nó rồi trải phẳng ra, ta được hình quạt tròn (Hình 6b). Tính theo r và l:
a) Độ dài cung BB’;
b) Số đo cung BB’;
c) Diện tích của hình quạt tròn.
Phương pháp giải:
Dựa vào tính độ dài cung, số đo cung và diện tích biểu diễn theo r và l.
Lời giải chi tiết:
a) Độ dài cung BB’ là: m = 2\(\pi \)r.
b) Số đo cung BB’ là: \(m = \frac{{\pi \ln }}{{180}}\) suy ra \(n = \frac{{180.m}}{{\pi {\mathop{\rm l}\nolimits} }}\).
c) Diện tích của hình quạt tròn là:
\(S = \frac{{n\pi {l^2}}}{{360}} = \frac{{\pi {l^2}}}{{360}}.\frac{{180.m}}{{\pi l}} = \frac{{l.m}}{2} = \frac{{2\pi rl}}{2} = \pi rl\).
Video hướng dẫn giải
Trả lời câu hỏi Thực hành 3 trang 90SGK Toán 9 Chân trời sáng tạo
Tính diện tích xung quanh và diện tích toàn phần của hình nón có đường kính đáy d = 10 m và chiều cao h = 12 m (kết quả làm tròn đến hàng phần trăm).
Phương pháp giải:
- Dựa vào diện tích xung quanh của hình nón có bán kính r, độ dài đường sinh l là: \({S_{xq}} = \pi rl\)
- Diện tích toàn phần \({S_{tp}} = {S_{xq}} + {S_{day}}\) để tính.
Lời giải chi tiết:
Bán kính của đáy là: \(r = \frac{d}{2} = \frac{10}{2} = 5 (m)\)
Ta có \(l = \sqrt {{r^2} + {h^2}} = \sqrt {{5^2} + {12^2}} = 13 (m).\)
Diện tích xung quanh là:
\({S_{xq}} = \pi rl = \pi .5.13 = 65 \pi\) (m2)
Diện tích toàn phần là:
\({S_{tp}} = {S_{xq}} + {S_{đáy}} = 65 \pi + \pi {r^2} = 65 \pi + \pi {.5^2} = 90\pi \approx\) 282, 74 m2.
Video hướng dẫn giải
Trả lời câu hỏi Hoạt động 2 trang 90 SGK Toán 9 Chân trời sáng tạo
Cho một hình nón có bán kính r, có độ dài đường sinh l (Hình 6a). Cắt mặt xung quanh của hình nón theo một đường sinh của nó rồi trải phẳng ra, ta được hình quạt tròn (Hình 6b). Tính theo r và l:
a) Độ dài cung BB’;
b) Số đo cung BB’;
c) Diện tích của hình quạt tròn.

Phương pháp giải:
Dựa vào tính độ dài cung, số đo cung và diện tích biểu diễn theo r và l.
Lời giải chi tiết:
a) Độ dài cung BB’ là: m = 2\(\pi \)r.
b) Số đo cung BB’ là: \(m = \frac{{\pi \ln }}{{180}}\) suy ra \(n = \frac{{180.m}}{{\pi {\mathop{\rm l}\nolimits} }}\).
c) Diện tích của hình quạt tròn là:
\(S = \frac{{n\pi {l^2}}}{{360}} = \frac{{\pi {l^2}}}{{360}}.\frac{{180.m}}{{\pi l}} = \frac{{l.m}}{2} = \frac{{2\pi rl}}{2} = \pi rl\).
Mục 2 trang 90 SGK Toán 9 tập 2 - Chân trời sáng tạo thường xoay quanh các bài toán liên quan đến hàm số bậc hai, bao gồm việc xác định hệ số, tìm đỉnh parabol, vẽ đồ thị hàm số và giải các bài toán ứng dụng thực tế. Việc nắm vững kiến thức về hàm số bậc hai là nền tảng quan trọng cho các chương trình học Toán ở các lớp trên.
Để giải quyết Mục 2 trang 90 SGK Toán 9 tập 2 - Chân trời sáng tạo một cách hiệu quả, chúng ta cần nắm vững các kiến thức sau:
Bài toán: Cho hàm số y = 2x2 - 4x + 1. Hãy tìm tọa độ đỉnh của parabol và vẽ đồ thị hàm số.
Giải:
| x | y |
|---|---|
| 0 | 1 |
| 1 | -1 |
| 2 | 1 |
Ngoài việc tìm tọa độ đỉnh và vẽ đồ thị, Mục 2 trang 90 SGK Toán 9 tập 2 - Chân trời sáng tạo còn xuất hiện các dạng bài tập sau:
Để giải các bài tập trong Mục 2 trang 90 SGK Toán 9 tập 2 - Chân trời sáng tạo một cách hiệu quả, bạn nên:
Hy vọng rằng với những hướng dẫn chi tiết và ví dụ minh họa trên, bạn đã có thể tự tin giải quyết Mục 2 trang 90 SGK Toán 9 tập 2 - Chân trời sáng tạo. Chúc bạn học tập tốt và đạt kết quả cao trong môn Toán!