Chào mừng các em học sinh đến với chuyên mục giải bài tập Toán 9 tập 2 của giaitoan.edu.vn. Ở bài viết này, chúng tôi sẽ cung cấp lời giải chi tiết và dễ hiểu cho các bài tập trong mục 2 trang 7 và 8 sách giáo khoa Toán 9 tập 2, chương trình Chân trời sáng tạo.
Mục tiêu của chúng tôi là giúp các em nắm vững kiến thức, rèn luyện kỹ năng giải toán và tự tin hơn trong các kỳ thi. Hãy cùng theo dõi và học tập nhé!
Cho hàm số (y = frac{1}{2}{x^2}). Hoàn thành bảng giá trị sau:
Video hướng dẫn giải
Trả lời câu hỏi Vận dụng 2 trang 8 SGK Toán 9 Chân trời sáng tạo
Một vật rơi tự do từ độ cao 125 m so với mặt đất. Quãng đường chuyển động s (m) của vật phụ thuộc và thời gian t (giây) được cho bởi công thức s = 5t2 .
a) Sau 2 (giây), vật này cách mặt đất bao nhiêu mét? Tương tự, sau 3 giây vật này cách mặt đất bao nhiêu mét?
b) Sau bao lâu thì vật này tiếp đất?
Phương pháp giải:
Thay lần lượt t = 2; t = 3 vào công thức s = 5t2 để tính quãng đường vật di chuyển được, từ đó tính được vật cách mặt đất bao nhiêu mét sau 2 giây, 3 giây theo công thức: 125 - s.
Thay s = 125 để thì tìm t.
Lời giải chi tiết:
a) Sau 2 giây quãng đường vật di chuyển được là:
s = 5.22 = 20 (m)
Sau 2 giây vật này cách mặt đất số mét là:
125 - s = 125 - 20 = 105 (m)
Sau 3 giây quãng đường vật di chuyển được là:
s = 5.32 = 45 (m)
Sau 3 giây vật này cách mặt đất số mét là:
125 - s = 125 - 45 = 80 (m)
b) Để vật này tiếp đất thì s = 125 thay vào 5t2 = 125
Do đó: t = 5 giây (vì t > 0)
Vậy sau 5 giây thì vật tiếp đất.
Video hướng dẫn giải
Trả lời câu hỏi Thực hành 2 trang 8 SGK Toán 9 Chân trời sáng tạo
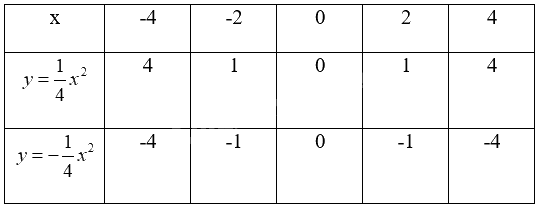
Lập bảng giá trị của hai hàm số \(y = \frac{1}{4}{x^2}\) và \(y = - \frac{1}{4}{x^2}\) với x lần lượt bằng – 4; -2; 0; 2; 4.
Phương pháp giải:
Thay lần lượt giá trị x vào hàm số \(y = \frac{1}{4}{x^2}\) và \(y = - \frac{1}{4}{x^2}\) để tính y.
Lời giải chi tiết:
Video hướng dẫn giải
Trả lời câu hỏi Hoạt động 2 trang 7 SGK Toán 9 Chân trời sáng tạo
Cho hàm số \(y = \frac{1}{2}{x^2}\). Hoàn thành bảng giá trị sau:

Phương pháp giải:
Thay lần lượt giá x vào hàm số \(y = \frac{1}{2}{x^2}\) để tính y.
Lời giải chi tiết:

Video hướng dẫn giải
Trả lời câu hỏi Hoạt động 2 trang 7 SGK Toán 9 Chân trời sáng tạo
Cho hàm số \(y = \frac{1}{2}{x^2}\). Hoàn thành bảng giá trị sau:

Phương pháp giải:
Thay lần lượt giá x vào hàm số \(y = \frac{1}{2}{x^2}\) để tính y.
Lời giải chi tiết:

Video hướng dẫn giải
Trả lời câu hỏi Thực hành 2 trang 8 SGK Toán 9 Chân trời sáng tạo
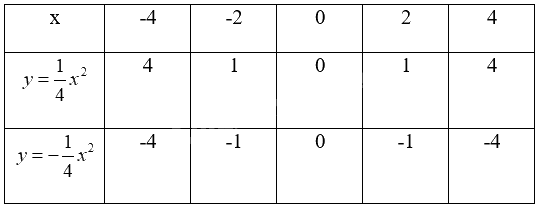
Lập bảng giá trị của hai hàm số \(y = \frac{1}{4}{x^2}\) và \(y = - \frac{1}{4}{x^2}\) với x lần lượt bằng – 4; -2; 0; 2; 4.
Phương pháp giải:
Thay lần lượt giá trị x vào hàm số \(y = \frac{1}{4}{x^2}\) và \(y = - \frac{1}{4}{x^2}\) để tính y.
Lời giải chi tiết:
Video hướng dẫn giải
Trả lời câu hỏi Vận dụng 2 trang 8 SGK Toán 9 Chân trời sáng tạo
Một vật rơi tự do từ độ cao 125 m so với mặt đất. Quãng đường chuyển động s (m) của vật phụ thuộc và thời gian t (giây) được cho bởi công thức s = 5t2 .
a) Sau 2 (giây), vật này cách mặt đất bao nhiêu mét? Tương tự, sau 3 giây vật này cách mặt đất bao nhiêu mét?
b) Sau bao lâu thì vật này tiếp đất?
Phương pháp giải:
Thay lần lượt t = 2; t = 3 vào công thức s = 5t2 để tính quãng đường vật di chuyển được, từ đó tính được vật cách mặt đất bao nhiêu mét sau 2 giây, 3 giây theo công thức: 125 - s.
Thay s = 125 để thì tìm t.
Lời giải chi tiết:
a) Sau 2 giây quãng đường vật di chuyển được là:
s = 5.22 = 20 (m)
Sau 2 giây vật này cách mặt đất số mét là:
125 - s = 125 - 20 = 105 (m)
Sau 3 giây quãng đường vật di chuyển được là:
s = 5.32 = 45 (m)
Sau 3 giây vật này cách mặt đất số mét là:
125 - s = 125 - 45 = 80 (m)
b) Để vật này tiếp đất thì s = 125 thay vào 5t2 = 125
Do đó: t = 5 giây (vì t > 0)
Vậy sau 5 giây thì vật tiếp đất.
Mục 2 của SGK Toán 9 tập 2 chương trình Chân trời sáng tạo tập trung vào việc ôn tập và hệ thống hóa kiến thức về hàm số bậc nhất. Các bài tập trong mục này thường yêu cầu học sinh vận dụng các kiến thức đã học để giải quyết các bài toán thực tế, đồng thời rèn luyện kỹ năng vẽ đồ thị hàm số và xác định các yếu tố của hàm số.
Bài 1 yêu cầu học sinh nhắc lại các khái niệm cơ bản về hàm số bậc nhất, bao gồm định nghĩa, dạng tổng quát, hệ số góc, giao điểm với các trục tọa độ. Ngoài ra, bài tập còn yêu cầu học sinh xác định hàm số bậc nhất từ các thông tin cho trước.
Bài 2 đưa ra một bài toán thực tế liên quan đến hàm số bậc nhất, yêu cầu học sinh xây dựng mô hình toán học và giải quyết bài toán. Ví dụ, bài toán có thể liên quan đến việc tính tiền điện, tính quãng đường đi được, hoặc tính lợi nhuận từ việc bán hàng.
Ví dụ:
Một người đi xe máy với vận tốc 40km/h. Hỏi sau 2 giờ người đó đi được quãng đường bao nhiêu?
Giải:
Gọi x là thời gian đi (giờ), y là quãng đường đi được (km). Ta có hàm số y = 40x. Khi x = 2, y = 40 * 2 = 80. Vậy sau 2 giờ người đó đi được 80km.
Bài 3 yêu cầu học sinh vẽ đồ thị của một số hàm số bậc nhất khác nhau. Để vẽ đồ thị, học sinh cần xác định ít nhất hai điểm thuộc đồ thị, sau đó nối hai điểm đó lại với nhau bằng một đường thẳng.
Ví dụ:
Vẽ đồ thị hàm số y = -2x + 1.
Giải:
Ngoài SGK Toán 9 tập 2, các em có thể tham khảo thêm các tài liệu sau để học tập và rèn luyện kỹ năng giải toán:
Hy vọng rằng với lời giải chi tiết và những lời khuyên hữu ích trên đây, các em học sinh sẽ tự tin hơn trong việc giải các bài tập trong mục 2 trang 7, 8 SGK Toán 9 tập 2 chương trình Chân trời sáng tạo. Chúc các em học tập tốt!