Giaitoan.edu.vn xin giới thiệu lời giải chi tiết mục 3 trang 101 SGK Toán 9 tập 1 - Chân trời sáng tạo. Bài viết này cung cấp đáp án chính xác, phương pháp giải rõ ràng, giúp học sinh nắm vững kiến thức và tự tin giải các bài tập tương tự.
Chúng tôi luôn cập nhật nhanh chóng và chính xác các lời giải bài tập Toán 9, đáp ứng nhu cầu học tập của học sinh trên toàn quốc.
a) Vẽ đường tròn (C) tâm O bán kính r = 5 cm và đường tròn (C’) tâm O bán kính R = 8 cm. b) Tính diện tích S của (C) và diện tích S’ của (C’). c) Hãy cho biết hiệu số (S’ – S) biểu diễn diện tích của phần nào trên Hình 9.
Video hướng dẫn giải
Trả lời câu hỏi Thực hành 3 trang 101 SGK Toán 9 Chân trời sáng tạo
Tính diện tích hình vành khuyên giới hạn bởi hai đường tròn (O; 10 cm) và (O; 20 cm) (kết quả làm tròn đến hàng phần trăm)
Phương pháp giải:
- Đọc kĩ dữ kiện để vẽ hình.
- Áp dụng diện tích hình vành khuyên giới hạn bởi hai đường tròn (O; r) và (O; R) là: \(S = \pi ({R^2} - {r^2})\)
Lời giải chi tiết:
Diện tích hình vành khuyên giới hạn bởi hai đường tròn (O; 10 cm) và (O; 20 cm) là:
\(S = \pi ({R^2} - {r^2}) = \pi ({20^2} - {10^2}) = 300\pi \approx 942,48\) cm2.
Video hướng dẫn giải
Trả lời câu hỏi Vận dụng 3 trang 101SGK Toán 9 Chân trời sáng tạo
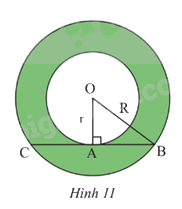
Cho hình vành khuyên giới hạn bởi hai đường tròn (O; r) và (O; R) với R > r. Trên đường tròn (O; R) lấy hai điểm B, C sao cho BC vừa là dây cung của (O; R), vừa là tiếp tuyến của đường tròn (O; r) tại A (Hình 11)
a) Tính độ dài đoạn thẳng BC theo r và R.
b) Cho BC = \(a\sqrt 3 \). Tính diện tích hình khuyên giới hạn bởi hai đường tròn (O; r) và (O; R) theo a.
Phương pháp giải:
- Dựa vào tính chất tiếp tuyến chứng minh OA \( \bot \)BC
- Tính BC bằng cách áp dụng định lý pythagore trong tam giác vuông
- Áp dụng diện tích hình vành khuyên giới hạn bởi hai đường tròn (O; r) và (O; R) là: \(S = \pi ({R^2} - {r^2})\)
Lời giải chi tiết:
a) Vì BC là tiếp tuyến của đường tròn (O; r) tại A nên OA \( \bot \)BC
Xét tam giác OAB vuông tại A , ta có:
AB = \(\sqrt {O{B^2} - O{A^2}} = \sqrt {{R^2} - {r^2}} \) (theo định lý Pythagore)
Tương tự với tam giác OCA vuông tại A, ta có
AC = \(\sqrt {O{C^2} - O{A^2}} = \sqrt {{R^2} - {r^2}} \) (theo định lý Pythagore)
Vậy BC = AB + AC = 2\(\sqrt {{R^2} - {r^2}} \).
b) Ta có BC = 2\(\sqrt {{R^2} - {r^2}} \) = \(a\sqrt 3 \) suy ra \(\sqrt {{R^2} - {r^2}} \) = \(\frac{{a\sqrt 3 }}{2}\)
Diện tích hình khuyên giới hạn bởi hai đường tròn (O; r) và (O; R) theo a là:
\(S = \pi ({R^2} - {r^2})\) = \(\pi {\left( {\frac{{a\sqrt 3 }}{2}} \right)^2} = \frac{{3\pi }}{4}{a^2}\).
Video hướng dẫn giải
Trả lời câu hỏi Hoạt động 3 trang 101 SGK Toán 9 Chân trời sáng tạo
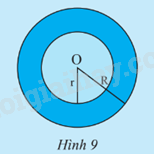
a) Vẽ đường tròn (C) tâm O bán kính r = 5 cm và đường tròn (C’) tâm O bán kính R = 8 cm.
b) Tính diện tích S của (C) và diện tích S’ của (C’).
c) Hãy cho biết hiệu số (S’ – S) biểu diễn diện tích của phần nào trên Hình 9.
Phương pháp giải:
- Đọc kĩ dữ kiện để vẽ hình.
- Dựa vào công thức diện tích đường tròn S =\(\pi \)R2
Lời giải chi tiết:
a) Ta có hình vẽ:
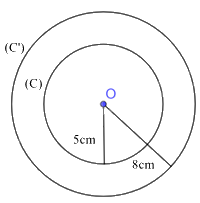
b) Diện tích S của (C) là: \(S = 5^2\pi = 25\pi \approx 78,54 (cm^2)\)
Diện tích S’ của (C’) là \(S’ = 8^2\pi = 64\pi \approx 201,06 (cm^2)\)
c) Hiệu số (S’ – S) biểu diễn diện tích của phần tô màu xanh đậm trong hình 9.
Video hướng dẫn giải
Trả lời câu hỏi Hoạt động 3 trang 101 SGK Toán 9 Chân trời sáng tạo
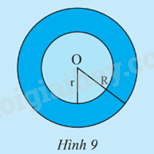
a) Vẽ đường tròn (C) tâm O bán kính r = 5 cm và đường tròn (C’) tâm O bán kính R = 8 cm.
b) Tính diện tích S của (C) và diện tích S’ của (C’).
c) Hãy cho biết hiệu số (S’ – S) biểu diễn diện tích của phần nào trên Hình 9.
Phương pháp giải:
- Đọc kĩ dữ kiện để vẽ hình.
- Dựa vào công thức diện tích đường tròn S =\(\pi \)R2
Lời giải chi tiết:
a) Ta có hình vẽ:
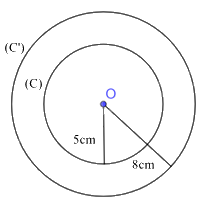
b) Diện tích S của (C) là: \(S = 5^2\pi = 25\pi \approx 78,54 (cm^2)\)
Diện tích S’ của (C’) là \(S’ = 8^2\pi = 64\pi \approx 201,06 (cm^2)\)
c) Hiệu số (S’ – S) biểu diễn diện tích của phần tô màu xanh đậm trong hình 9.
Video hướng dẫn giải
Trả lời câu hỏi Thực hành 3 trang 101 SGK Toán 9 Chân trời sáng tạo
Tính diện tích hình vành khuyên giới hạn bởi hai đường tròn (O; 10 cm) và (O; 20 cm) (kết quả làm tròn đến hàng phần trăm)
Phương pháp giải:
- Đọc kĩ dữ kiện để vẽ hình.
- Áp dụng diện tích hình vành khuyên giới hạn bởi hai đường tròn (O; r) và (O; R) là: \(S = \pi ({R^2} - {r^2})\)
Lời giải chi tiết:
Diện tích hình vành khuyên giới hạn bởi hai đường tròn (O; 10 cm) và (O; 20 cm) là:
\(S = \pi ({R^2} - {r^2}) = \pi ({20^2} - {10^2}) = 300\pi \approx 942,48\) cm2.
Video hướng dẫn giải
Trả lời câu hỏi Vận dụng 3 trang 101SGK Toán 9 Chân trời sáng tạo
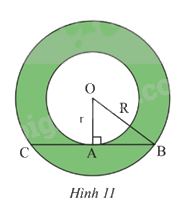
Cho hình vành khuyên giới hạn bởi hai đường tròn (O; r) và (O; R) với R > r. Trên đường tròn (O; R) lấy hai điểm B, C sao cho BC vừa là dây cung của (O; R), vừa là tiếp tuyến của đường tròn (O; r) tại A (Hình 11)
a) Tính độ dài đoạn thẳng BC theo r và R.
b) Cho BC = \(a\sqrt 3 \). Tính diện tích hình khuyên giới hạn bởi hai đường tròn (O; r) và (O; R) theo a.
Phương pháp giải:
- Dựa vào tính chất tiếp tuyến chứng minh OA \( \bot \)BC
- Tính BC bằng cách áp dụng định lý pythagore trong tam giác vuông
- Áp dụng diện tích hình vành khuyên giới hạn bởi hai đường tròn (O; r) và (O; R) là: \(S = \pi ({R^2} - {r^2})\)
Lời giải chi tiết:
a) Vì BC là tiếp tuyến của đường tròn (O; r) tại A nên OA \( \bot \)BC
Xét tam giác OAB vuông tại A , ta có:
AB = \(\sqrt {O{B^2} - O{A^2}} = \sqrt {{R^2} - {r^2}} \) (theo định lý Pythagore)
Tương tự với tam giác OCA vuông tại A, ta có
AC = \(\sqrt {O{C^2} - O{A^2}} = \sqrt {{R^2} - {r^2}} \) (theo định lý Pythagore)
Vậy BC = AB + AC = 2\(\sqrt {{R^2} - {r^2}} \).
b) Ta có BC = 2\(\sqrt {{R^2} - {r^2}} \) = \(a\sqrt 3 \) suy ra \(\sqrt {{R^2} - {r^2}} \) = \(\frac{{a\sqrt 3 }}{2}\)
Diện tích hình khuyên giới hạn bởi hai đường tròn (O; r) và (O; R) theo a là:
\(S = \pi ({R^2} - {r^2})\) = \(\pi {\left( {\frac{{a\sqrt 3 }}{2}} \right)^2} = \frac{{3\pi }}{4}{a^2}\).
Mục 3 trang 101 SGK Toán 9 tập 1 - Chân trời sáng tạo thường xoay quanh các chủ đề về hàm số bậc nhất, đồ thị hàm số, và ứng dụng của hàm số trong giải quyết các bài toán thực tế. Việc nắm vững kiến thức về hàm số bậc nhất là nền tảng quan trọng cho các chương trình học Toán ở các lớp trên.
Để hiểu rõ hơn về nội dung mục 3 trang 101, chúng ta cần xem xét các phần sau:
Các bài tập trong mục 3 trang 101 thường yêu cầu học sinh:
Để giải các bài tập trong mục 3 trang 101, học sinh cần:
Bài tập: Cho hàm số y = 2x - 1. Hãy vẽ đồ thị của hàm số này.
Giải:
Để học tốt môn Toán 9, đặc biệt là phần hàm số bậc nhất, học sinh nên:
Ngoài SGK Toán 9 tập 1 - Chân trời sáng tạo, học sinh có thể tham khảo thêm các tài liệu sau:
Hy vọng rằng bài viết này đã cung cấp cho bạn những kiến thức hữu ích về cách giải mục 3 trang 101 SGK Toán 9 tập 1 - Chân trời sáng tạo. Chúc bạn học tập tốt và đạt kết quả cao trong môn Toán!