Chào mừng bạn đến với bài học lý thuyết Phương trình quy về phương trình bậc nhất một ẩn trong chương trình Toán 9 Chân trời sáng tạo. Bài học này sẽ cung cấp cho bạn những kiến thức nền tảng quan trọng để giải quyết các bài toán liên quan đến phương trình.
Chúng ta sẽ cùng nhau tìm hiểu về cách nhận biết, biến đổi và giải các phương trình phức tạp bằng cách đưa chúng về dạng phương trình bậc nhất một ẩn quen thuộc.
1. Phương trình tích Phương trình tích là phương trình có dạng \(\left( {ax + b} \right)\left( {cx + d} \right) = 0\).
1. Phương trình tích
Phương trình tích là phương trình có dạng \(\left( {ax + b} \right)\left( {cx + d} \right) = 0\).
Cách giải phương trình tích
Muốn giải phương trình tích \(\left( {ax + b} \right)\left( {cx + d} \right) = 0\), ta giải hai phương trình \(ax + b = 0\) và \(cx + d = 0\), rồi lấy tất cả các nghiệm của chúng. |
Ví dụ:Giải phương trình \(\left( {2x + 1} \right)\left( {3x - 1} \right) = 0\)
Lời giải:
Ta có: \(\left( {2x + 1} \right)\left( {3x - 1} \right) = 0\)
\(2x + 1 = 0\) hoặc \(3x - 1 = 0\).
\(2x = - 1\) hoặc \(3x = 1\)
\(x = - \frac{1}{2}\) hoặc \(x = \frac{1}{3}\)
Vậy phương trình đã cho có hai nghiệm là \(x = - \frac{1}{2}\) và \(x = \frac{1}{3}\).
Các bước giải phương trình:
Bước 1. Đưa phương trình về phương trình tích \(\left( {ax + b} \right)\left( {cx + d} \right) = 0\). Bước 2. Giải phương trình tích tìm được. |
Ví dụ: Giải phương trình \({x^2} - x = - 2x + 2\).
Lời giải:
Biến đổi phương trình đã cho về phương trình tích như sau:
\(\begin{array}{l}{x^2} - x = - 2x + 2\\{x^2} - x + 2x - 2 = 0\\x\left( {x - 1} \right) + 2\left( {x - 1} \right) = 0\\\left( {x + 2} \right)\left( {x - 1} \right) = 0.\end{array}\)
\(x + 2 = 0\) hoặc \(x - 1 = 0\).
\(x = - 2\) hoặc \(x = 1\).
Vậy phương trình đã cho có hai nghiệm là \(x = - 2\) và \(x = 1\).
2. Phương trình chứa ẩn ở mẫu quy về phương trình bậc nhất
Điều kiện xác định của phương trình chứa ẩn ở mẫu
Đối với phương trình chứa ẩn ở mẫu, điều kiện của ẩn để tất cả các mẫu thức trong phương trình đều khác 0 gọi là điều kiện xác định của phương trình. |
Ví dụ:
- Phương trình \(\frac{{5x + 2}}{{x - 1}} = 0\) có điều kiện xác định là \(x \ne 1\) vì \(x - 1 \ne 0\) khi \(x \ne 1\).
- Phương trình \(\frac{1}{{x + 1}} = 1 + \frac{1}{{x - 2}}\) có điều kiện xác định là \(x \ne - 1\) và \(x \ne 2\) vì \(x + 1 \ne 0\) khi \(x \ne - 1\), \(x - 2 \ne 0\) khi \(x \ne 2\).
Các bước giải phương trình chứa ẩn ở mẫu
Bước 1. Tìm điều kiện xác định của phương trình. Bước 2. Quy đồng mẫu thức hai vế của phương trình, rồi khử mẫu. Bước 3. Giải phương trình vừa tìm được. Bước 4. Xét mỗi giá trị tìm được ở Bước 3, giá trị nào thỏa mãn điều kiện xác định chính là nghiệm của phương trình đã cho. |
Ví dụ: Giải phương trình \(\frac{2}{{x + 1}} + \frac{1}{{x - 2}} = \frac{3}{{\left( {x + 1} \right)\left( {x - 2} \right)}}\)
Lời giải:
Điều kiện xác định \(x \ne - 1\) và \(x \ne 2\).
Ta có: \(\frac{2}{{x + 1}} + \frac{1}{{x - 2}} = \frac{3}{{\left( {x + 1} \right)\left( {x - 2} \right)}}\)
\(\frac{{2\left( {x - 2} \right) + \left( {x + 1} \right)}}{{\left( {x + 1} \right)\left( {x - 2} \right)}} = \frac{3}{{\left( {x + 1} \right)\left( {x - 2} \right)}}\)
\(2\left( {x - 2} \right) + \left( {x + 1} \right) = 3\)
\(\begin{array}{l}2\left( {x - 2} \right) + \left( {x + 1} \right) = 3\\2x - 4 + x + 1 = 3\\3x - 3 = 3\\3x = 6\\x = 2\end{array}\)
Giá trị \(x = 2\) không thỏa mãn ĐKXĐ.
Vậy phương trình \(\frac{2}{{x + 1}} + \frac{1}{{x - 2}} = \frac{3}{{\left( {x + 1} \right)\left( {x - 2} \right)}}\) vô nghiệm.
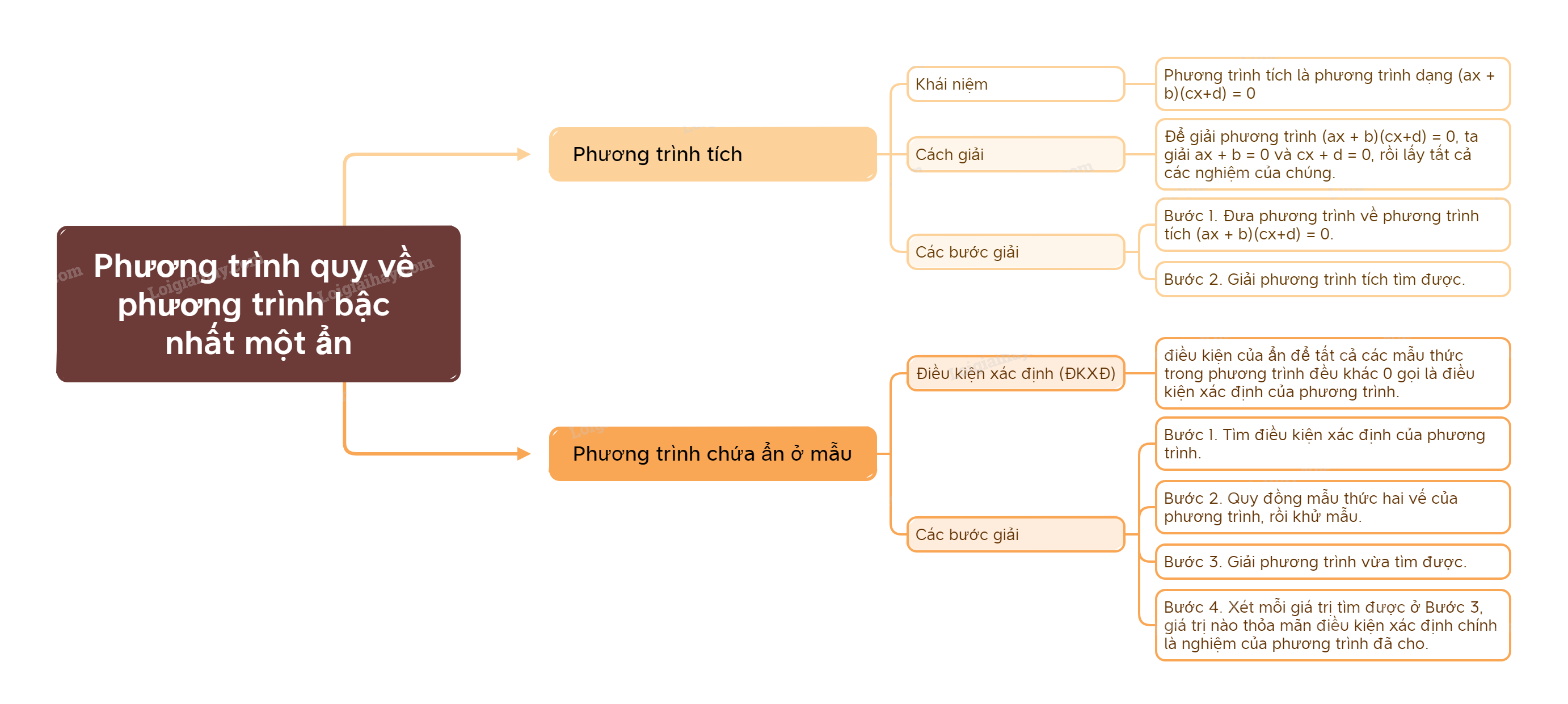
Trong chương trình Toán 9, việc nắm vững kiến thức về phương trình là vô cùng quan trọng. Một trong những dạng phương trình thường gặp là phương trình quy về phương trình bậc nhất một ẩn. Bài viết này sẽ cung cấp một cách chi tiết và dễ hiểu về lý thuyết này, giúp các em học sinh Chân trời sáng tạo có thể tự tin giải quyết các bài toán liên quan.
Trước khi đi sâu vào phương trình quy về bậc nhất một ẩn, chúng ta cần hiểu rõ phương trình bậc nhất một ẩn là gì. Phương trình bậc nhất một ẩn có dạng tổng quát là:
ax + b = 0
Trong đó:
Nghiệm của phương trình là giá trị của x sao cho phương trình trở thành một đẳng thức.
Phương trình quy về phương trình bậc nhất một ẩn là những phương trình có dạng phức tạp hơn, nhưng có thể được biến đổi về dạng phương trình bậc nhất một ẩn bằng các phép biến đổi tương đương.
Các dạng phương trình thường gặp quy về phương trình bậc nhất một ẩn:
Ví dụ 1: Giải phương trình (2x + 1)(x - 3) = 0
Giải:
Phương trình tương đương với:
2x + 1 = 0 hoặc x - 3 = 0
Từ 2x + 1 = 0 suy ra x = -1/2
Từ x - 3 = 0 suy ra x = 3
Vậy phương trình có hai nghiệm là x = -1/2 và x = 3.
Ví dụ 2: Giải phương trình (x + 2) / (x - 1) = 0
Giải:
Điều kiện xác định: x ≠ 1
Phương trình tương đương với x + 2 = 0
Suy ra x = -2
Vì x = -2 thỏa mãn điều kiện xác định, nên phương trình có nghiệm duy nhất x = -2.
Để củng cố kiến thức, các em hãy tự giải các bài tập sau:
Hy vọng bài viết này đã cung cấp cho các em những kiến thức hữu ích về lý thuyết Phương trình quy về phương trình bậc nhất một ẩn Toán 9 Chân trời sáng tạo. Chúc các em học tập tốt!