Giaitoan.edu.vn xin giới thiệu lời giải chi tiết mục 3 trang 40 SGK Toán 9 tập 1 - Chân trời sáng tạo. Bài giải được trình bày rõ ràng, dễ hiểu, giúp học sinh nắm vững kiến thức và rèn luyện kỹ năng giải toán.
Chúng tôi luôn cập nhật nhanh chóng và chính xác các bài giải Toán 9 tập 1, đáp ứng nhu cầu học tập của học sinh trên toàn quốc.
Một chiếc thang dài 5m tựa vào bức tường như Hình 3. a) Nếu chân thang cách chân tường x (m) thì đỉnh thang ở độ cao bao nhiêu so với chân tường? b) Tính độ cao trên khi x nhận giá trị lần lượt là 1;2;3;4.
Video hướng dẫn giải
Trả lời câu hỏi Thực hành 7 trang 40 SGK Toán 9 Chân trời sáng tạo
Với giá trị nào của x thì biểu thức A = \(\sqrt {3x + 6} \) xác định? Tính giá trị của A khi x = 5 (kết quả làm tròn đến chữ số thập phân thứ hai).
Phương pháp giải:
Tìm ĐKXĐ của \(\sqrt A \) khi và chỉ khi \(A \ge 0\)
Thay x = 5 vào biểu thức A để tính
Lời giải chi tiết:
ĐKXĐ: 3x + 6 \( \ge \) 0 suy ra x \( \ge \) - 2
Thay x = 5 vào A = \(\sqrt {3x + 6} \), ta được: A = \(\sqrt {3.5 + 6} = \sqrt {21} \approx 4,58\)
Video hướng dẫn giải
Trả lời câu hỏi Thực hành 8 trang 40 SGK Toán 9 Chân trời sáng tạo
Cho biểu thức P = \(\sqrt {{a^2} - {b^2}} \). Tính giá trị của P khi:
a) a = 5; b = 0
b) a = 5; b = -5
c) a = 2; b = -4
Phương pháp giải:
Thay lần lượt a và b vào biểu thức P để tính.
Lời giải chi tiết:
a) Thay a = 5; b = 0 vào P = \(\sqrt {{a^2} - {b^2}} \), ta được:
P = \(\sqrt {{5^2} - {0^2}} = 5\)
b) Thay a = 5; b = -5 vào P = \(\sqrt {{a^2} - {b^2}} \), ta được:
P = \(\sqrt {{5^2} - {{( - 5)}^2}} = 0\)
c) Thay a = 2; b = -4 vào P = \(\sqrt {{a^2} - {b^2}} \) thì biểu thức P không khác định vì
a2 – b2 = -12 < 0 .
Video hướng dẫn giải
Trả lời câu hỏi Vận dụng 2 trang 40 SGK Toán 9 Chân trời sáng tạo
Một trạm phát sóng được đặt ở vị trí B cách đường tàu một khoảng AB = 300 m. Đầu tàu đang ở vị trí C, cách vị trí A một khoảng AC = x (m) (Hình 4)
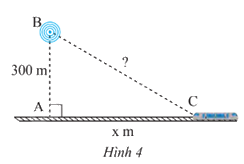
a) Viết biểu thức (theo x) biểu thị khoảng cách từ trạm phát sóng đến đầu tàu.
b) Tính khoảng cách trên khi x = 400; x = 1000 (kết quả làm tròn đến hàng đơn vị của mét).
Phương pháp giải:
Sử dụng định lí Pythagore vào tam giac vuông ABC có:
BC2 = AB2 + AC2.
Thay lần lượt giá trị x để tính khoảng cách
Lời giải chi tiết:
a) Ta có khoảng cách từ trạm phát sóng đến đầu tàu là: \(\sqrt {{{300}^2} + {x^2}} \) (m)
b) Thay x = 400 thì khoảng cách từ trạm phát sóng đến đầu tàu là: \(\sqrt {{{300}^2} + {{400}^2}} = 500\) (m)
Thay x = 1000 thì khoảng cách từ trạm phát sóng đến đầu tàu là: \(\sqrt {{{300}^2} + {{1000}^2}} \approx 1044\) (m)
Video hướng dẫn giải
Trả lời câu hỏi Hoạt động 2 trang 40SGK Toán 9 Chân trời sáng tạo
Một chiếc thang dài 5m tựa vào bức tường như Hình 3.
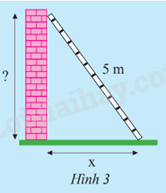
a) Nếu chân thang cách chân tường x (m) thì đỉnh thang ở độ cao bao nhiêu so với chân tường?
b) Tính độ cao trên khi x nhận giá trị lần lượt là 1;2;3;4.
Phương pháp giải:
Áp dụng định lý Pythagore vào tam giác vuông tạo bởi chiếc thang và bức tường.
Thay lần lượt từng giá trị x để tính độ cao.
Lời giải chi tiết:
a) Đỉnh thang có độ cao là: \(\sqrt {{5^2} - {x^2}} \) (m).
b) Khi x = 1 thì độ cao là \(\sqrt {{5^2} - {1^2}} = 2\sqrt 6 \) (m)
Khi x = 2 thì độ cao là \(\sqrt {{5^2} - {2^2}} = \sqrt {21} \)(m)
Khi x = 3 thì độ cao là \(\sqrt {{5^2} - {3^2}} = 4\)(m)
Khi x = 4 thì độ cao là \(\sqrt {{5^2} - {4^2}} = 3\)(m)
Video hướng dẫn giải
Trả lời câu hỏi Hoạt động 2 trang 40SGK Toán 9 Chân trời sáng tạo
Một chiếc thang dài 5m tựa vào bức tường như Hình 3.
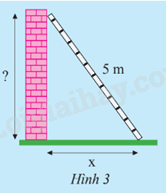
a) Nếu chân thang cách chân tường x (m) thì đỉnh thang ở độ cao bao nhiêu so với chân tường?
b) Tính độ cao trên khi x nhận giá trị lần lượt là 1;2;3;4.
Phương pháp giải:
Áp dụng định lý Pythagore vào tam giác vuông tạo bởi chiếc thang và bức tường.
Thay lần lượt từng giá trị x để tính độ cao.
Lời giải chi tiết:
a) Đỉnh thang có độ cao là: \(\sqrt {{5^2} - {x^2}} \) (m).
b) Khi x = 1 thì độ cao là \(\sqrt {{5^2} - {1^2}} = 2\sqrt 6 \) (m)
Khi x = 2 thì độ cao là \(\sqrt {{5^2} - {2^2}} = \sqrt {21} \)(m)
Khi x = 3 thì độ cao là \(\sqrt {{5^2} - {3^2}} = 4\)(m)
Khi x = 4 thì độ cao là \(\sqrt {{5^2} - {4^2}} = 3\)(m)
Video hướng dẫn giải
Trả lời câu hỏi Thực hành 7 trang 40 SGK Toán 9 Chân trời sáng tạo
Với giá trị nào của x thì biểu thức A = \(\sqrt {3x + 6} \) xác định? Tính giá trị của A khi x = 5 (kết quả làm tròn đến chữ số thập phân thứ hai).
Phương pháp giải:
Tìm ĐKXĐ của \(\sqrt A \) khi và chỉ khi \(A \ge 0\)
Thay x = 5 vào biểu thức A để tính
Lời giải chi tiết:
ĐKXĐ: 3x + 6 \( \ge \) 0 suy ra x \( \ge \) - 2
Thay x = 5 vào A = \(\sqrt {3x + 6} \), ta được: A = \(\sqrt {3.5 + 6} = \sqrt {21} \approx 4,58\)
Video hướng dẫn giải
Trả lời câu hỏi Thực hành 8 trang 40 SGK Toán 9 Chân trời sáng tạo
Cho biểu thức P = \(\sqrt {{a^2} - {b^2}} \). Tính giá trị của P khi:
a) a = 5; b = 0
b) a = 5; b = -5
c) a = 2; b = -4
Phương pháp giải:
Thay lần lượt a và b vào biểu thức P để tính.
Lời giải chi tiết:
a) Thay a = 5; b = 0 vào P = \(\sqrt {{a^2} - {b^2}} \), ta được:
P = \(\sqrt {{5^2} - {0^2}} = 5\)
b) Thay a = 5; b = -5 vào P = \(\sqrt {{a^2} - {b^2}} \), ta được:
P = \(\sqrt {{5^2} - {{( - 5)}^2}} = 0\)
c) Thay a = 2; b = -4 vào P = \(\sqrt {{a^2} - {b^2}} \) thì biểu thức P không khác định vì
a2 – b2 = -12 < 0 .
Video hướng dẫn giải
Trả lời câu hỏi Vận dụng 2 trang 40 SGK Toán 9 Chân trời sáng tạo
Một trạm phát sóng được đặt ở vị trí B cách đường tàu một khoảng AB = 300 m. Đầu tàu đang ở vị trí C, cách vị trí A một khoảng AC = x (m) (Hình 4)
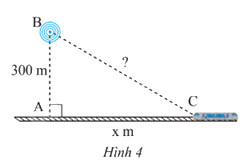
a) Viết biểu thức (theo x) biểu thị khoảng cách từ trạm phát sóng đến đầu tàu.
b) Tính khoảng cách trên khi x = 400; x = 1000 (kết quả làm tròn đến hàng đơn vị của mét).
Phương pháp giải:
Sử dụng định lí Pythagore vào tam giac vuông ABC có:
BC2 = AB2 + AC2.
Thay lần lượt giá trị x để tính khoảng cách
Lời giải chi tiết:
a) Ta có khoảng cách từ trạm phát sóng đến đầu tàu là: \(\sqrt {{{300}^2} + {x^2}} \) (m)
b) Thay x = 400 thì khoảng cách từ trạm phát sóng đến đầu tàu là: \(\sqrt {{{300}^2} + {{400}^2}} = 500\) (m)
Thay x = 1000 thì khoảng cách từ trạm phát sóng đến đầu tàu là: \(\sqrt {{{300}^2} + {{1000}^2}} \approx 1044\) (m)
Mục 3 trang 40 SGK Toán 9 tập 1 - Chân trời sáng tạo thường xoay quanh các bài toán liên quan đến hàm số bậc nhất, đặc biệt là việc xác định hệ số góc và đường thẳng song song, vuông góc. Việc nắm vững kiến thức về hàm số bậc nhất là nền tảng quan trọng để giải quyết các bài toán này một cách hiệu quả.
Bài học này tập trung vào việc:
Để giải các bài toán trong Mục 3 trang 40 SGK Toán 9 tập 1 - Chân trời sáng tạo, học sinh cần:
Bài tập 1: Xác định hệ số góc của đường thẳng y = -2x + 5.
Lời giải: Hệ số góc của đường thẳng y = -2x + 5 là a = -2.
Bài tập 2: Tìm phương trình đường thẳng song song với đường thẳng y = 3x - 1 và đi qua điểm A(1; 2).
Lời giải: Đường thẳng song song với y = 3x - 1 có dạng y = 3x + b. Thay tọa độ điểm A(1; 2) vào phương trình, ta có: 2 = 3 * 1 + b => b = -1. Vậy phương trình đường thẳng cần tìm là y = 3x - 1.
Bài tập 3: Tìm phương trình đường thẳng vuông góc với đường thẳng y = -1/2x + 3 và đi qua điểm B(0; -2).
Lời giải: Đường thẳng vuông góc với y = -1/2x + 3 có hệ số góc là a = 2. Vậy phương trình đường thẳng cần tìm có dạng y = 2x + b. Thay tọa độ điểm B(0; -2) vào phương trình, ta có: -2 = 2 * 0 + b => b = -2. Vậy phương trình đường thẳng cần tìm là y = 2x - 2.
Ngoài các bài toán cơ bản, học sinh có thể gặp các bài toán phức tạp hơn, đòi hỏi sự kết hợp kiến thức về hàm số bậc nhất với các kiến thức khác như hệ phương trình, bất phương trình. Để giải quyết các bài toán này, học sinh cần rèn luyện kỹ năng tư duy logic và khả năng vận dụng kiến thức một cách linh hoạt.
Để củng cố kiến thức và kỹ năng giải toán, học sinh nên luyện tập thêm các bài tập tương tự trong SGK, sách bài tập và các nguồn tài liệu khác. Việc luyện tập thường xuyên sẽ giúp học sinh nắm vững kiến thức và tự tin hơn khi làm bài kiểm tra.
Giải mục 3 trang 40 SGK Toán 9 tập 1 - Chân trời sáng tạo đòi hỏi học sinh nắm vững kiến thức về hàm số bậc nhất và các phương pháp giải toán liên quan. Bằng cách áp dụng đúng công thức, rèn luyện kỹ năng tư duy và luyện tập thường xuyên, học sinh có thể giải quyết các bài toán một cách hiệu quả và đạt kết quả tốt trong học tập.