Chào mừng bạn đến với giaitoan.edu.vn, nơi cung cấp lời giải chi tiết và dễ hiểu cho các bài tập Toán 9 tập 1 - Chân trời sáng tạo. Bài tập 16 trang 73 là một trong những bài tập quan trọng giúp học sinh củng cố kiến thức về các khái niệm đã học.
Chúng tôi hiểu rằng việc giải bài tập Toán đôi khi có thể gặp khó khăn. Vì vậy, đội ngũ giáo viên giàu kinh nghiệm của chúng tôi đã biên soạn lời giải chi tiết, kèm theo các bước giải rõ ràng, giúp bạn nắm vững phương pháp và tự tin giải các bài tập tương tự.
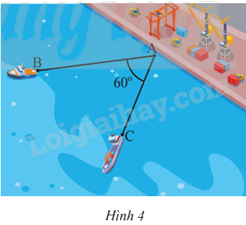
Hai điểm tàu thủy B và C cùng xuất phát từ một vị trí A, đi thẳng theo hai hướng tạo thành một góc 60o (Hình 4). Tàu B chạy với tốc độ 20 hải lí/giờ, tàu C chạy với tốc độ 15 hải lý/giờ. Hỏi sau 1,5 giờ hai tàu B và C cách nhau bao nhiêu hải lí (kết quả làm tròn đến hàng phần trăm)?
Đề bài
Hai điểm tàu thủy B và C cùng xuất phát từ một vị trí A, đi thẳng theo hai hướng tạo thành một góc 60o (Hình 4). Tàu B chạy với tốc độ 20 hải lí/giờ, tàu C chạy với tốc độ 15 hải lý/giờ. Hỏi sau 1,5 giờ hai tàu B và C cách nhau bao nhiêu hải lí (kết quả làm tròn đến hàng phần trăm)?
Video hướng dẫn giải
Phương pháp giải - Xem chi tiết
- Áp dụng công thức S = v.t để tính quãng đường tàu B và C đi được sau 1,5 giờ
- Dựa vào định lí: Xét tam giác vuông, mỗi cạnh góc vuông bằng cạnh huyền nhân sin góc đối hoặc nhân côsin góc kề rồi suy ra cạnh góc vuông.
- Áp dụng định lý Pythagore lần lượt vào 2 tam giác vuông ACH và CHB để tìm ra BC.
Lời giải chi tiết
Sau 1,5 giờ tàu B đi được 1,5.20 = 30 hải lý, tàu C đi được 1,5.15 = 22,5 hải lý.
Kẻ CH vuông góc với AB (\(H \in AB\)). Ta có hình vẽ sau:
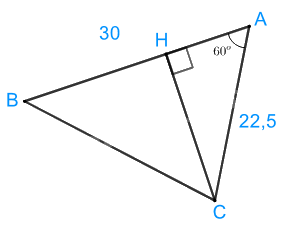
Xét tam giác AHC vuông tại H, có:
CH = AC. sin 60o = 22,5. sin 60o = \(\frac{45\sqrt 3}{4} \) (hải lý)
Áp dụng định lý Pythagore ta có:
AH = \(\sqrt {{{22,5}^2} - {{\left( {\frac{45\sqrt 3}{4}} \right)}^2}} = \frac{45}{4}\) (hải lý)
Suy ra \(BH = 30 – \frac{45}{4} = \frac{75}{4}\) (hải lý)
Mặt khác, tam giác CHB vuông tại H, áp dụng định lý Pythagore ta có:
BC = \(\sqrt {C{H^2} + B{H^2}} = \sqrt {{{\left( {\frac{45\sqrt 3}{4} } \right)}^2} + \left( \frac{75}{4}\right)}^2 = \frac{15\sqrt13}{2} \approx 27,04\) (hải lý)
Vậy sau 1,5 giờ hai tàu B và C cách nhau 27,04 hải lý.
Bài tập 16 trang 73 SGK Toán 9 tập 1 - Chân trời sáng tạo thuộc chương trình học về hàm số bậc nhất. Bài tập này yêu cầu học sinh vận dụng kiến thức về hàm số bậc nhất để giải quyết các bài toán thực tế, liên quan đến việc xác định hệ số góc và đường thẳng song song, vuông góc.
Bài tập 16 bao gồm các câu hỏi nhỏ, yêu cầu học sinh:
Để giải bài tập 16 trang 73 SGK Toán 9 tập 1 - Chân trời sáng tạo một cách hiệu quả, học sinh cần nắm vững các kiến thức sau:
Câu a: Xác định hệ số góc của đường thẳng y = 2x - 3.
Lời giải: Hệ số góc của đường thẳng y = 2x - 3 là a = 2.
Câu b: Tìm m để đường thẳng y = (m - 1)x + 2 song song với đường thẳng y = 3x + 1.
Lời giải: Để hai đường thẳng song song, ta cần có m - 1 = 3 và 2 ≠ 1. Suy ra m = 4.
Câu c: Tìm m để đường thẳng y = (2m + 1)x - 5 vuông góc với đường thẳng y = -x + 3.
Lời giải: Để hai đường thẳng vuông góc, ta cần có (2m + 1)(-1) = -1. Suy ra 2m + 1 = 1, do đó m = 0.
Xét đường thẳng y = -x + 5. Hệ số góc của đường thẳng này là -1. Đường thẳng này đi xuống và có độ dốc lớn hơn so với đường thẳng y = 0.5x + 2.
Để củng cố kiến thức về hàm số bậc nhất và các điều kiện song song, vuông góc, bạn có thể tự giải thêm các bài tập sau:
Bài tập 16 trang 73 SGK Toán 9 tập 1 - Chân trời sáng tạo là một bài tập quan trọng giúp học sinh hiểu rõ hơn về hàm số bậc nhất và các ứng dụng của nó. Hy vọng với lời giải chi tiết và phương pháp giải rõ ràng mà giaitoan.edu.vn cung cấp, bạn sẽ tự tin giải quyết bài tập này và các bài tập tương tự một cách hiệu quả.