Chào mừng bạn đến với bài học về Lý thuyết Hình trụ trong chương trình Toán 9 Chân trời sáng tạo tại giaitoan.edu.vn. Bài viết này sẽ cung cấp đầy đủ kiến thức cơ bản, công thức quan trọng và các ví dụ minh họa để giúp bạn hiểu rõ về hình trụ.
Chúng ta sẽ cùng nhau khám phá định nghĩa, các yếu tố của hình trụ, cách tính diện tích xung quanh, diện tích toàn phần và thể tích của hình trụ.
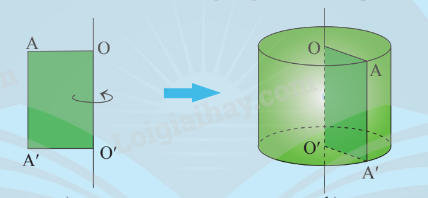
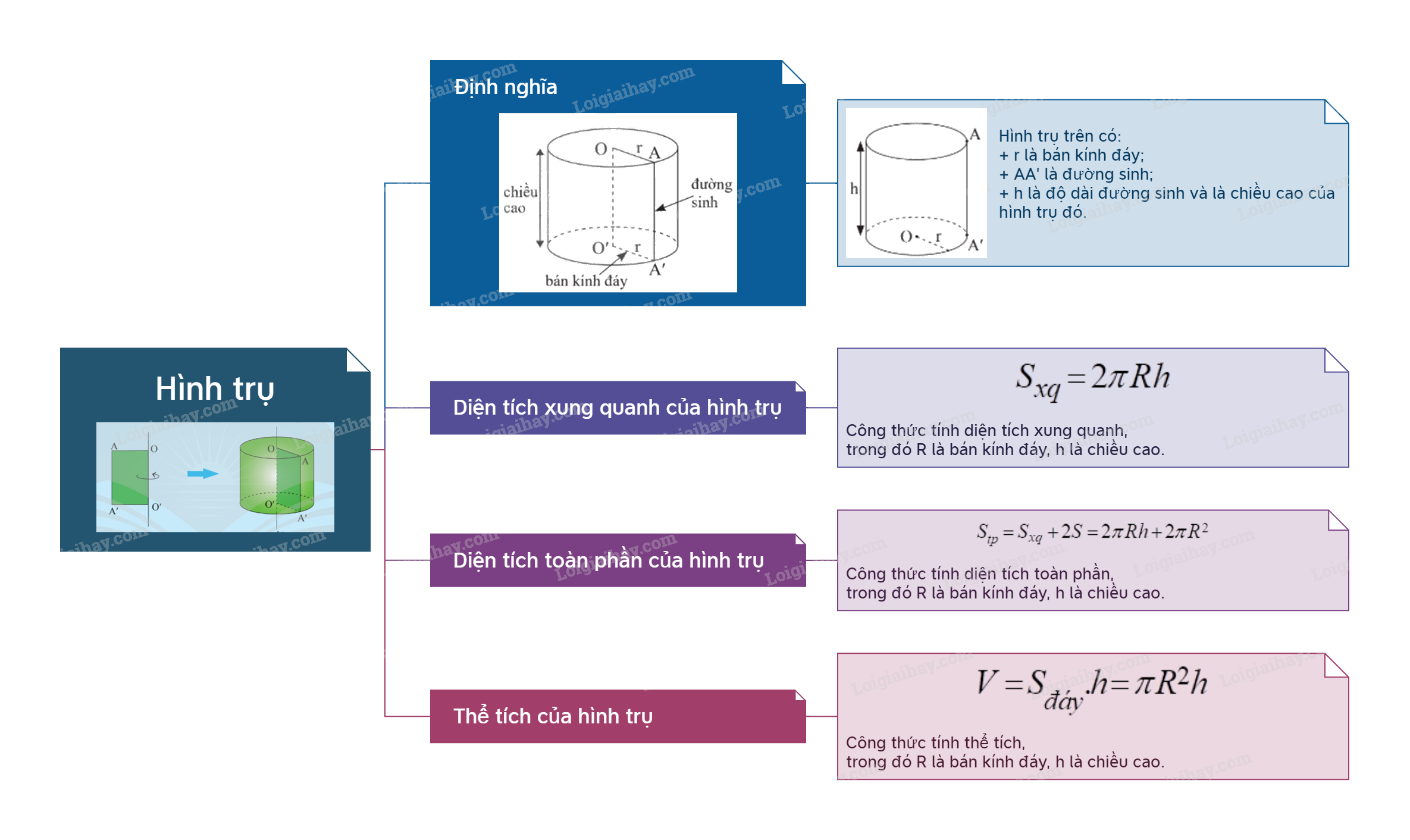
1. Hình trụ Định nghĩa Khi quay hình chữ nhật AA'O'O một vòng quanh cạnh OO' cố định ta được một hình trụ. − Cạnh OA, O′A′ quét thành hai hình tròn có cùng bán kính gọi là hai đáy của hình trụ; bán kính của đáy gọi là bán kính đáy của hình trụ. – Cạnh AA′ quét thành mặt xung quanh của hình trụ, mỗi vị trí của AA' được coi là một đường sinh. – Độ dài đoạn OO' gọi là chiều cao của hình trụ. Các đường sinh có độ dài bằng nhau và bằng chiều cao của hình trụ.
1. Hình trụ
Định nghĩa
Khi quay hình chữ nhật AA'O'O một vòng quanh cạnh OO' cố định ta được một hình trụ.
− Cạnh OA, O′A′ quét thành hai hình tròn có cùng bán kính gọi là hai đáy của hình trụ; bán kính của đáy gọi là bán kính đáy của hình trụ. – Cạnh AA′ quét thành mặt xung quanh của hình trụ, mỗi vị trí của AA' được coi là một đường sinh. – Độ dài đoạn OO' gọi là chiều cao của hình trụ. Các đường sinh có độ dài bằng nhau và bằng chiều cao của hình trụ. |
Ví dụ:
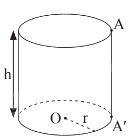
Hình trụ trên có:
+ r là bán kính đáy;
+ AA’ là đường sinh;
+ h là độ dài đường sinh và là chiều cao của hình trụ đó.
2. Diện tích xung quanh của hình trụ
Diện tích xung quanh của hình trụ
Diện tích xung quanh \({S_{xq}}\) của hình trụ có bán kính đáy r và chiều cao h là: \({S_{xq}} = 2\pi rh\). |
Diện tích toàn phần của hình trụ
Diện tích toàn phần \({S_{tp}}\) của hình trụ có bán kính đáy r và chiều cao h là: \({S_{tp}} = {S_{xq}} + 2S = 2\pi rh + 2\pi {r^2}\) (S là diện tích đáy của hình trụ). |
Ví dụ:
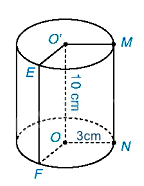
Diện tích xung quanh của hình trụ là:
\({S_{xq}} = 2\pi rh = 2\pi .3.10 = 60\pi \left( {c{m^2}} \right)\)
3. Thể tích của hình trụ
Thể tích V của hình trụ có bán kính đáy r và chiều cao h là: \(V = S.h = \pi {r^2}h\) (S là diện tích đáy của hình trụ).
|
Ví dụ:
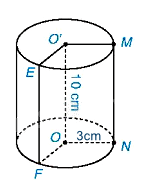
Diện tích đáy là:
\(S = \pi {r^2} = \pi {.3^2} = 9\pi \left( {c{m^2}} \right)\)
Thể tích của hình trụ là:
\(V = S.h = 9\pi .10 = 90\pi \left( {c{m^3}} \right)\)
Hình trụ là một trong những hình học quan trọng trong chương trình Toán 9, đặc biệt là trong sách Chân trời sáng tạo. Việc nắm vững lý thuyết và các công thức liên quan đến hình trụ là nền tảng để giải quyết các bài toán thực tế và đạt kết quả tốt trong các kỳ thi.
Hình trụ là một hình hình học được tạo thành bởi hai hình tròn bằng nhau và song song, gọi là hai đáy, và một mặt bên là mặt xung quanh. Mặt xung quanh là một mặt cong được tạo thành bởi một đường thẳng di chuyển song song với hai đáy.
Diện tích xung quanh của hình trụ (Sxq) được tính bằng công thức:
Sxq = 2πrh
Trong đó:
Diện tích toàn phần của hình trụ (Stp) được tính bằng công thức:
Stp = Sxq + 2πr2
Hoặc:
Stp = 2πrh + 2πr2
Trong đó:
Thể tích của hình trụ (V) được tính bằng công thức:
V = πr2h
Trong đó:
Ví dụ 1: Một hình trụ có bán kính đáy là 5cm và chiều cao là 10cm. Tính diện tích xung quanh, diện tích toàn phần và thể tích của hình trụ đó.
Giải:
Ví dụ 2: Một hình trụ có diện tích toàn phần là 628.32 cm2 và chiều cao là 10cm. Tính bán kính đáy của hình trụ đó.
Giải:
Ta có: Stp = 2πrh + 2πr2
=> 628.32 = 2 * 3.14159 * r * 10 + 2 * 3.14159 * r2
=> 628.32 = 62.8318r + 6.28318r2
=> 6.28318r2 + 62.8318r - 628.32 = 0
Giải phương trình bậc hai này, ta được r = 5 cm.
Hy vọng bài viết này đã cung cấp cho bạn những kiến thức cơ bản và hữu ích về Lý thuyết Hình trụ Toán 9 Chân trời sáng tạo. Chúc bạn học tập tốt!