Chào mừng các em học sinh đến với bài giải chi tiết mục 3 trang 87, 88 SGK Toán 9 tập 1 - Chân trời sáng tạo trên giaitoan.edu.vn. Bài viết này sẽ cung cấp lời giải đầy đủ, dễ hiểu cho từng bài tập, giúp các em nắm vững kiến thức và tự tin hơn trong quá trình học tập.
Chúng tôi luôn cố gắng mang đến những giải pháp học tập hiệu quả nhất, hỗ trợ các em học sinh chinh phục môn Toán một cách dễ dàng.
Cho đường tròn O và hai tiếp tuyến của đường tròn (O) tại B và C cắt nhau tại điểm A (Hình 10). a) Chứng minh hai tam giác ABO và ACO bằng nhau. b) Tìm các đoạn thẳng bằng nhau và các góc bằng nhau trong Hình 10.
Video hướng dẫn giải
Trả lời câu hỏi Hoạt động 3 trang 87SGK Toán 9 Chân trời sáng tạo
Cho đường tròn O và hai tiếp tuyến của đường tròn (O) tại B và C cắt nhau tại điểm A (Hình 10).
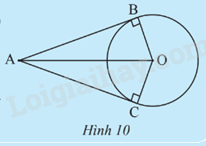
a) Chứng minh hai tam giác ABO và ACO bằng nhau.
b) Tìm các đoạn thẳng bằng nhau và các góc bằng nhau trong Hình 10.
Phương pháp giải:
- Dựa vào chứng minh 2 tam giác bằng nhau theo cạnh huyền - cạnh góc vuông.
- Vì 2 tam giác bằng nhau nên các góc và các cạnh trong tam giác bằng nhau.
Lời giải chi tiết:
a) Xét tam giác ABO và ACO có:
\(\widehat {ABO} = \widehat {ACO} = {90^o}\)
AO chung
OB = OC = R
Suy ra \(\Delta \)ABO = \(\Delta \)ACO (cạnh huyền - cạnh góc vuông)
b) Theo Hình 10, ta có: \(\Delta \)ABO = \(\Delta \)ACO
suy ra AB = AC; BO = CO
\(\begin{array}{l}\widehat {ABO} = \widehat {ACO} = {90^o}\\\widehat {BAO} = \widehat {CAO}\\\widehat {AOB} = \widehat {AOC}\end{array}\)
Video hướng dẫn giải
Trả lời câu hỏi Thực hành 3 trang 87SGK Toán 9 Chân trời sáng tạo
Cho điểm M nằm ngoài đường tròn (I; 6 cm) và ME, MF là hai tiếp tuyến của đường tròn này tại E và F. Cho biết \(\widehat {EMF} = {60^o}\).
a) Tính số đo \(\widehat {EMI}\) và \(\widehat {EIF}\) .
b) Tính độ dài MI.
Phương pháp giải:
- Dựa vào dữ kiện đề bài để vẽ hình.
- Dựa vào định lí: Nếu hai tiếp tuyến của một đường tròn cắt nhau tại 1 điểm thì tia kẻ từ điểm đó đi qua tâm là tia phân giác của góc tạo bởi hai tiếp tuyến để tính \(\widehat {EMI}\). Tính \(\widehat {EIF}\) dựa vào tính chất trong một tứ giác tổng các góc bằng 360o.
- Tính MI áp dụng tỉ số lượng giác trong tam giác vuông MIE: Tỉ số giữa cạnh đối và cạnh huyền được gọi là sin.
Lời giải chi tiết:
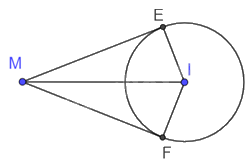
a) Ta có hai tiếp tuyến ME và MF cắt nhau tại M nên MI là tia phân giác \(\widehat {EMF}\).
Suy ra \(\widehat {EMI} = \frac{{\widehat {EMF}}}{2} = \frac{{{{60}^o}}}{2} = {30^o}\).
Xét tứ giác MEFI ta có
\(\begin{array}{l}\widehat {EIF} = {360^o} - (\widehat {EMF} + \widehat {MFI} + \widehat {MEI})\\ = {360^o} - (\widehat {EMF} + 2\widehat {MFI})\\ = {360^o} - ({60^o} + {2.90^o})\\ = {120^o}\end{array}\)
b) Xét tam giác MEI vuông tại E, MI = 6 cm; \(\widehat {EMI} = {30^o}\) ta có
sin \(\widehat {EMI}\) = \(\frac{{EI}}{{MI}}\) suy ra MI = \(\frac{{EI}}{{\sin \widehat {EMI}}} = \frac{6}{{\sin {{30}^o}}} = 12\)cm.
Video hướng dẫn giải
Trả lời câu hỏi Thực hành 4 trang 88SGK Toán 9 Chân trời sáng tạo
Tìm giá trị x trong Hình 12.
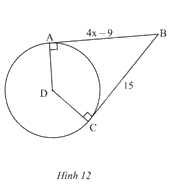
Phương pháp giải:
Chứng minh BA và BC là tiếp tuyến cùa đường tròn (D; DA).
Suy ra AB = BC để tìm x.
Lời giải chi tiết:
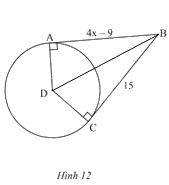
Nối B với D.
Vì BA \(\bot\) DA tại A; BC \(\bot\) DC tại C nên BA và BC là hai tiếp tuyến của đường tròn (D; DA).
Hai tiếp tuyến BA và BC cắt nhau tại B nên BA = BC.
hay 4x – 9 = 15 suy ra x = 6.
Video hướng dẫn giải
Trả lời câu hỏi Hoạt động 3 trang 87SGK Toán 9 Chân trời sáng tạo
Cho đường tròn O và hai tiếp tuyến của đường tròn (O) tại B và C cắt nhau tại điểm A (Hình 10).
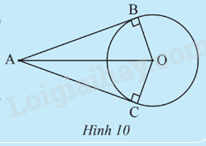
a) Chứng minh hai tam giác ABO và ACO bằng nhau.
b) Tìm các đoạn thẳng bằng nhau và các góc bằng nhau trong Hình 10.
Phương pháp giải:
- Dựa vào chứng minh 2 tam giác bằng nhau theo cạnh huyền - cạnh góc vuông.
- Vì 2 tam giác bằng nhau nên các góc và các cạnh trong tam giác bằng nhau.
Lời giải chi tiết:
a) Xét tam giác ABO và ACO có:
\(\widehat {ABO} = \widehat {ACO} = {90^o}\)
AO chung
OB = OC = R
Suy ra \(\Delta \)ABO = \(\Delta \)ACO (cạnh huyền - cạnh góc vuông)
b) Theo Hình 10, ta có: \(\Delta \)ABO = \(\Delta \)ACO
suy ra AB = AC; BO = CO
\(\begin{array}{l}\widehat {ABO} = \widehat {ACO} = {90^o}\\\widehat {BAO} = \widehat {CAO}\\\widehat {AOB} = \widehat {AOC}\end{array}\)
Video hướng dẫn giải
Trả lời câu hỏi Thực hành 3 trang 87SGK Toán 9 Chân trời sáng tạo
Cho điểm M nằm ngoài đường tròn (I; 6 cm) và ME, MF là hai tiếp tuyến của đường tròn này tại E và F. Cho biết \(\widehat {EMF} = {60^o}\).
a) Tính số đo \(\widehat {EMI}\) và \(\widehat {EIF}\) .
b) Tính độ dài MI.
Phương pháp giải:
- Dựa vào dữ kiện đề bài để vẽ hình.
- Dựa vào định lí: Nếu hai tiếp tuyến của một đường tròn cắt nhau tại 1 điểm thì tia kẻ từ điểm đó đi qua tâm là tia phân giác của góc tạo bởi hai tiếp tuyến để tính \(\widehat {EMI}\). Tính \(\widehat {EIF}\) dựa vào tính chất trong một tứ giác tổng các góc bằng 360o.
- Tính MI áp dụng tỉ số lượng giác trong tam giác vuông MIE: Tỉ số giữa cạnh đối và cạnh huyền được gọi là sin.
Lời giải chi tiết:
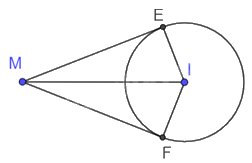
a) Ta có hai tiếp tuyến ME và MF cắt nhau tại M nên MI là tia phân giác \(\widehat {EMF}\).
Suy ra \(\widehat {EMI} = \frac{{\widehat {EMF}}}{2} = \frac{{{{60}^o}}}{2} = {30^o}\).
Xét tứ giác MEFI ta có
\(\begin{array}{l}\widehat {EIF} = {360^o} - (\widehat {EMF} + \widehat {MFI} + \widehat {MEI})\\ = {360^o} - (\widehat {EMF} + 2\widehat {MFI})\\ = {360^o} - ({60^o} + {2.90^o})\\ = {120^o}\end{array}\)
b) Xét tam giác MEI vuông tại E, MI = 6 cm; \(\widehat {EMI} = {30^o}\) ta có
sin \(\widehat {EMI}\) = \(\frac{{EI}}{{MI}}\) suy ra MI = \(\frac{{EI}}{{\sin \widehat {EMI}}} = \frac{6}{{\sin {{30}^o}}} = 12\)cm.
Video hướng dẫn giải
Trả lời câu hỏi Thực hành 4 trang 88SGK Toán 9 Chân trời sáng tạo
Tìm giá trị x trong Hình 12.
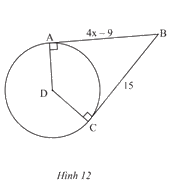
Phương pháp giải:
Chứng minh BA và BC là tiếp tuyến cùa đường tròn (D; DA).
Suy ra AB = BC để tìm x.
Lời giải chi tiết:
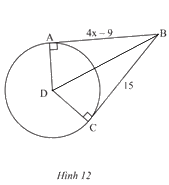
Nối B với D.
Vì BA \(\bot\) DA tại A; BC \(\bot\) DC tại C nên BA và BC là hai tiếp tuyến của đường tròn (D; DA).
Hai tiếp tuyến BA và BC cắt nhau tại B nên BA = BC.
hay 4x – 9 = 15 suy ra x = 6.
Video hướng dẫn giải
Trả lời câu hỏi Vận dụng 3 trang 88SGK Toán 9 Chân trời sáng tạo
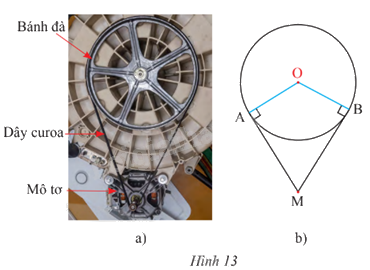
Bánh đà của một động cơ được thiết kế có dạng một đường tròn tâm O, bán kính 15 cm được kéo bởi một dây curoa. Trục của mô tơ truyền lực được biểu diễn bởi điểm M (Hình 13). Cho biết khoảng cách OM là 35 cm.
a) Tính độ dài của hai đoạn dây curoa MA và MB (kết quả làm tròn đến hàng phần mười).
b) Tính số đo \(\widehat {AMB}\) tạo bởi hai tiếp tuyến AM, BM và số đo \(\widehat {AOB}\) (kết quả làm tròn đến phút).
Phương pháp giải:
- Áp dụng định lý Pythagore vào tam giác AOM vuông tại A để tính MA suy ra MB.
- Áp dụng tỉ số lượng giác trong tam giác vuông AMO: Tỉ số giữa cạnh đối và cạnh kề được gọi là tan. Sau đó dùng máy tính bấm ra góc \(\widehat {AMO}\) suy ra góc \(\widehat {AMB}\). Tính \(\widehat {AOB}\) bằng cách dựa vào tính chất trong một tứ giác tổng các góc bằng 360o.
Lời giải chi tiết:
a) Áp dụng định lý Pythagore vào tam giác AOM vuông tại A, ta có:
MA = \(\sqrt {O{M^2} - O{A^2}} = \sqrt {{{35}^2} - {{15}^2}} = 31,6cm\)
MA và MB là hai tiếp tuyến của (O; 15cm) cắt nhau tại M nên MA = MB = 31,6 cm.
b) Ta có \(\widehat {AMB}\) tạo bởi hai tiếp tuyến AM, BM có MO là phân giác nên \(\widehat {AMB}\) = 2\(\widehat {AMO}\).
Xét tam giác AOM vuông tại A, ta có:
sin \(\widehat {AMO}\) = \(\frac{{AO}}{{MO}} = \frac{{15}}{{35}} = \frac{3}{7}\)
suy ra \(\widehat {AMO} \approx {25^o}23'\) nên \(\widehat {AMB}\)= 2\(\widehat {AMO} \approx {50^o}46'\)
\(\begin{array}{l}\widehat {AOB} = {360^o} - (2\widehat {AOM} + \widehat {AMB})\\ = {360^o} - ({2.90^o} + {50^o}46')\\ = {129^o}14'\end{array}\)
Video hướng dẫn giải
Trả lời câu hỏi Vận dụng 3 trang 88SGK Toán 9 Chân trời sáng tạo
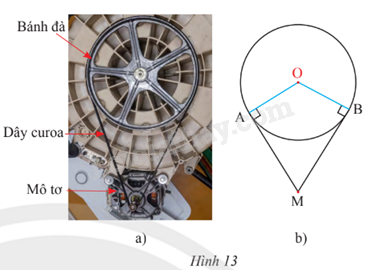
Bánh đà của một động cơ được thiết kế có dạng một đường tròn tâm O, bán kính 15 cm được kéo bởi một dây curoa. Trục của mô tơ truyền lực được biểu diễn bởi điểm M (Hình 13). Cho biết khoảng cách OM là 35 cm.
a) Tính độ dài của hai đoạn dây curoa MA và MB (kết quả làm tròn đến hàng phần mười).
b) Tính số đo \(\widehat {AMB}\) tạo bởi hai tiếp tuyến AM, BM và số đo \(\widehat {AOB}\) (kết quả làm tròn đến phút).
Phương pháp giải:
- Áp dụng định lý Pythagore vào tam giác AOM vuông tại A để tính MA suy ra MB.
- Áp dụng tỉ số lượng giác trong tam giác vuông AMO: Tỉ số giữa cạnh đối và cạnh kề được gọi là tan. Sau đó dùng máy tính bấm ra góc \(\widehat {AMO}\) suy ra góc \(\widehat {AMB}\). Tính \(\widehat {AOB}\) bằng cách dựa vào tính chất trong một tứ giác tổng các góc bằng 360o.
Lời giải chi tiết:
a) Áp dụng định lý Pythagore vào tam giác AOM vuông tại A, ta có:
MA = \(\sqrt {O{M^2} - O{A^2}} = \sqrt {{{35}^2} - {{15}^2}} = 31,6cm\)
MA và MB là hai tiếp tuyến của (O; 15cm) cắt nhau tại M nên MA = MB = 31,6 cm.
b) Ta có \(\widehat {AMB}\) tạo bởi hai tiếp tuyến AM, BM có MO là phân giác nên \(\widehat {AMB}\) = 2\(\widehat {AMO}\).
Xét tam giác AOM vuông tại A, ta có:
sin \(\widehat {AMO}\) = \(\frac{{AO}}{{MO}} = \frac{{15}}{{35}} = \frac{3}{7}\)
suy ra \(\widehat {AMO} \approx {25^o}23'\) nên \(\widehat {AMB}\)= 2\(\widehat {AMO} \approx {50^o}46'\)
\(\begin{array}{l}\widehat {AOB} = {360^o} - (2\widehat {AOM} + \widehat {AMB})\\ = {360^o} - ({2.90^o} + {50^o}46')\\ = {129^o}14'\end{array}\)
Mục 3 trong SGK Toán 9 tập 1 - Chân trời sáng tạo tập trung vào việc ôn tập và củng cố kiến thức về hàm số bậc nhất. Các bài tập trong mục này thường yêu cầu học sinh vận dụng các kiến thức đã học để giải quyết các bài toán thực tế, rèn luyện kỹ năng tư duy logic và khả năng giải quyết vấn đề.
Bài tập này yêu cầu học sinh xác định các hệ số a, b trong hàm số bậc nhất y = ax + b dựa vào các thông tin cho trước, chẳng hạn như đồ thị hàm số hoặc các điểm thuộc đồ thị.
Ví dụ: Cho đồ thị hàm số đi qua hai điểm A(0; 2) và B(1; 5). Hãy xác định hàm số bậc nhất.
Lời giải: Vì đồ thị đi qua A(0; 2) nên b = 2. Thay x = 1, y = 5 vào hàm số y = ax + 2, ta có: 5 = a(1) + 2 => a = 3. Vậy hàm số bậc nhất là y = 3x + 2.
Bài tập này yêu cầu học sinh vẽ đồ thị hàm số bậc nhất dựa vào các thông tin cho trước, chẳng hạn như hệ số a, b hoặc các điểm thuộc đồ thị.
Ví dụ: Vẽ đồ thị hàm số y = -2x + 1.
Lời giải: Xác định hai điểm thuộc đồ thị, chẳng hạn như A(0; 1) và B(1; -1). Vẽ đường thẳng đi qua hai điểm này, ta được đồ thị hàm số y = -2x + 1.
Bài tập này yêu cầu học sinh tìm tọa độ giao điểm của hai đường thẳng bằng phương pháp giải hệ phương trình bậc nhất hai ẩn.
Ví dụ: Tìm tọa độ giao điểm của hai đường thẳng y = 2x - 1 và y = -x + 2.
Lời giải: Giải hệ phương trình:
Thay y = 2x - 1 vào phương trình thứ hai, ta có: 2x - 1 = -x + 2 => 3x = 3 => x = 1. Thay x = 1 vào phương trình y = 2x - 1, ta có: y = 2(1) - 1 = 1. Vậy tọa độ giao điểm là (1; 1).
Bài tập này yêu cầu học sinh vận dụng kiến thức về hàm số bậc nhất để giải quyết các bài toán thực tế, chẳng hạn như tính tiền điện, tính quãng đường đi được, tính lợi nhuận,...
Ví dụ: Một người đi xe máy với vận tốc 40km/h. Hỏi sau 2 giờ người đó đi được quãng đường bao nhiêu?
Lời giải: Gọi s là quãng đường đi được, t là thời gian đi. Ta có hàm số s = 40t. Thay t = 2 vào hàm số, ta có: s = 40(2) = 80. Vậy sau 2 giờ người đó đi được quãng đường 80km.
Ngoài SGK Toán 9 tập 1 - Chân trời sáng tạo, các em có thể tham khảo thêm các tài liệu sau:
Hy vọng bài giải chi tiết mục 3 trang 87, 88 SGK Toán 9 tập 1 - Chân trời sáng tạo trên giaitoan.edu.vn sẽ giúp các em học sinh hiểu rõ hơn về hàm số bậc nhất và tự tin hơn trong quá trình học tập. Chúc các em học tốt!