Giaitoan.edu.vn xin giới thiệu lời giải chi tiết bài tập 7 trang 74 SGK Toán 9 tập 2 - Chân trời sáng tạo. Bài viết này sẽ giúp học sinh nắm vững kiến thức, hiểu rõ phương pháp giải và tự tin làm bài tập.
Chúng tôi cung cấp đáp án chính xác, dễ hiểu, kèm theo các bước giải cụ thể, giúp bạn dễ dàng theo dõi và áp dụng vào các bài tập tương tự. Hãy cùng giaitoan.edu.vn khám phá lời giải chi tiết ngay sau đây!
Cho hình vuông ABCD có độ dài cạnh bằng a. Góc vuông xAy thay đổi sao cho tia Ax cắt đoạn thẳng BC tại M và tia Ay cắt đoạn thẳng CD kéo dài tại N. a) Chứng minh hai tam giác ABM và ADN bằng nhau. b) Gọi O là trung điểm của MN. Chứng minh ABMO và ANDO là các tứ giác nội tiếp. c) Chứng minh ba điểm B, D, O thẳng hàng.
Đề bài
Cho hình vuông ABCD có độ dài cạnh bằng a. Góc vuông xAy thay đổi sao cho tia Ax cắt đoạn thẳng BC tại M và tia Ay cắt đoạn thẳng CD kéo dài tại N.
a) Chứng minh hai tam giác ABM và ADN bằng nhau.
b) Gọi O là trung điểm của MN. Chứng minh ABMO và ANDO là các tứ giác nội tiếp.
c) Chứng minh ba điểm B, D, O thẳng hàng.
Video hướng dẫn giải
Phương pháp giải - Xem chi tiết
- Đọc kĩ dữ liệu để vẽ hình.
- Chứng minh \(\Delta \)ABM = \(\Delta \)ADN (g.c.g)
- Hai tam giác vuông có cùng cạnh huyền thì tứ giác có đỉnh là các đỉnh của hai tam giác vuông nội tiếp đường tròn đường kính là cạnh huyền.
- Chứng minh O là tâm đường tròn ngoại tiếp tứ giác AMCN. Suy ra
OA = OC. Sau đó chứng minh B, D, O cùng thuộc trung trực của đoạn thẳng AC. Vậy ba điểm B, D, O thẳng hàng.
Lời giải chi tiết
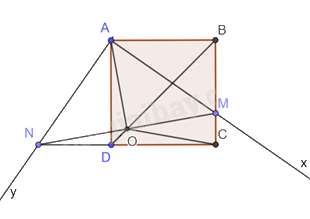
a) Xét \(\Delta \)ABM và \(\Delta \)ADN ta có:
AB = AD
\(\widehat {ABM} = \widehat {ADN}( = {90^o})\)
\(\widehat {BAM} = \widehat {NAD}\)(cùng phụ với \(\widehat {DAM}\))
Do đó \(\Delta \)ABM = \(\Delta \)ADN (g.c.g)
b) Ta có AM = AN (do \(\Delta \)ABM = \(\Delta \)ADN)
Suy ra \(\Delta \) AMN cân tại A
Mà AO cũng là đường trung tuyến (O là trung điểm của NM)
Nên AO cũng là đường cao suy ra AO \( \bot \) NM tại O.
Tam giác ABM vuông tại B và tam giác AOM vuông tại O cùng nội tiếp đường tròn đường kính AM nên tứ giác ABMO là tứ giác nội tiếp đường tròn đường kính AM.
Tam giác ADN vuông tại D và tam giác AON vuông tại O cùng nội tiếp đường tròn đường kính AN nên tứ giác AODN là tứ giác nội tiếp đường tròn đường kính AN.
c) Tam giác NAM vuông tại A (do góc xAy vuông) và tam giác NCM vuông tại C cùng nội tiếp đường tròn đường kính MN nên tứ giác AMCN là tứ giác nội tiếp đường tròn đường kính MN.
Điểm O là trung điểm của MN nên O là tâm đường tròn ngoại tiếp tứ giác AMCN.
Suy ra OA = OC suy ra O thuộc đường trung trực của AC.
Mà DA = DC, BA = BC (tứ giác ABCD là hình vuông) nên D và B thuộc đường trung trực của AC.
Do đó B, D, O cùng thuộc trung trực của đoạn thẳng AC.
Vậy ba điểm B, D, O thẳng hàng.
Bài tập 7 trang 74 SGK Toán 9 tập 2 - Chân trời sáng tạo thuộc chương trình học Toán 9, tập trung vào việc vận dụng kiến thức về hàm số bậc nhất và hàm số bậc hai để giải quyết các bài toán thực tế. Bài tập này yêu cầu học sinh phải hiểu rõ các khái niệm về hệ số góc, giao điểm của đồ thị hàm số và khả năng ứng dụng của hàm số trong việc mô tả các hiện tượng vật lý, kinh tế.
Trước khi bắt đầu giải bài tập, học sinh cần đọc kỹ đề bài, xác định rõ yêu cầu của bài toán. Trong bài tập 7 trang 74, yêu cầu thường là tìm hệ số góc của đường thẳng, xác định phương trình đường thẳng đi qua hai điểm cho trước, hoặc tìm giao điểm của hai đường thẳng. Việc phân tích đề bài chính xác sẽ giúp học sinh lựa chọn phương pháp giải phù hợp và tránh sai sót.
Để giải bài tập 7 trang 74, học sinh cần nắm vững các phương pháp sau:
(Ở đây sẽ là lời giải chi tiết cho từng phần của bài tập 7, bao gồm các bước giải, giải thích và kết luận. Ví dụ:)
Ví dụ: Cho đường thẳng y = 2x + 1. Hãy xác định hệ số góc của đường thẳng này.
Giải: Hệ số góc của đường thẳng y = 2x + 1 là a = 2. Vì a > 0, đường thẳng này đồng biến.
Ngoài bài tập 7 trang 74, còn rất nhiều bài tập tương tự trong SGK Toán 9 tập 2 - Chân trời sáng tạo. Để giải các bài tập này, học sinh có thể áp dụng các phương pháp đã học và luyện tập thường xuyên. Dưới đây là một số dạng bài tập tương tự:
Khi giải bài tập hàm số bậc nhất và bậc hai, học sinh cần lưu ý những điều sau:
Hàm số bậc nhất và bậc hai có rất nhiều ứng dụng trong thực tế, ví dụ như:
Bài tập 7 trang 74 SGK Toán 9 tập 2 - Chân trời sáng tạo là một bài tập quan trọng giúp học sinh củng cố kiến thức về hàm số bậc nhất và bậc hai. Hy vọng rằng với hướng dẫn chi tiết này, các em học sinh sẽ tự tin giải quyết bài tập và đạt kết quả tốt trong môn Toán.
Giaitoan.edu.vn luôn đồng hành cùng các em trên con đường chinh phục kiến thức Toán học. Chúc các em học tập tốt!