Chào mừng bạn đến với giaitoan.edu.vn, nơi cung cấp lời giải chi tiết và dễ hiểu cho các bài tập Toán 9 tập 1 - Chân trời sáng tạo. Bài tập 14 trang 105 là một trong những bài tập quan trọng giúp học sinh củng cố kiến thức về các khái niệm đã học.
Chúng tôi hiểu rằng việc giải bài tập Toán đôi khi có thể gặp khó khăn. Vì vậy, đội ngũ giáo viên giàu kinh nghiệm của chúng tôi đã biên soạn lời giải chi tiết, kèm theo các bước giải rõ ràng, giúp bạn dễ dàng nắm bắt kiến thức và tự tin giải các bài tập tương tự.
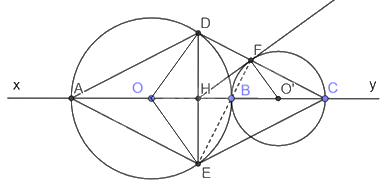
Trên đường thẳng xy, lấy lần lượt ba điểm A, B, C sao cho AB > BC. Vẽ đường tròn (O) đường kính AB và đường tròn (O’) đường kính BC. a) Chứng minh rằng hai đường tròn (O) và (O’) tiếp xúc ngoài B. b) Gọi H là trung điểm AC. Vẽ dây DE của (O) vuông góc với AC tại H. Chứng minh tứ giác ADCE là hình thoi. c) DC cắt đường tròn (O’) tại F. Chứng minh rằng ba điểm F, B, E thẳng hàng. d) Chứng minh rằng HF là tiếp tuyến của đường tròn (O’).
Đề bài
Trên đường thẳng xy, lấy lần lượt ba điểm A, B, C sao cho AB > BC. Vẽ đường tròn (O) đường kính AB và đường tròn (O’) đường kính BC.
a) Chứng minh rằng hai đường tròn (O) và (O’) tiếp xúc ngoài B.
b) Gọi H là trung điểm AC. Vẽ dây DE của (O) vuông góc với AC tại H. Chứng minh tứ giác ADCE là hình thoi.
c) DC cắt đường tròn (O’) tại F. Chứng minh rằng ba điểm F, B, E thẳng hàng.
d) Chứng minh rằng HF là tiếp tuyến của đường tròn (O’).
Video hướng dẫn giải
Phương pháp giải - Xem chi tiết
Đọc kĩ dữ liệu để vẽ hình.
a) Dựa vào: Vị trí tương đối của hai đường tròn để chứng minh
b) Chứng minh tứ giác ADCE là hình bình hành có AC\( \bot \)DE nên ADCE là hình thoi.
c) Chứng minh EB và FB trùng nhau nên ba điểm F, B, E thẳng hàng.
d) Chứng minh HF\( \bot \)O’F và F thuộc (O’) nên HF là tiếp tuyến của đường tròn (O’).
Lời giải chi tiết
a) Ta có OO’ = OB + BO’ (d = R + R’)
Do đó đường tròn (O) và đường tròn (O’) tiếp xúc ngoài.
b) Xét tam giác DOE có OD = OE = R nên tam giác DOE cân tại O.
Vì \(OH \bot DE\) nên OH vừa là đường cao đồng thời là đường trung tuyến của tam giác DOE.
Suy ra H là trung điểm của DE.
Xét tứ giác ADCE có:
AC cắt DE tại H,
H là trung điểm của AC,
H là trung điểm của DE
Do đó tứ giác ADCE là hình bình hành.
Mặt khác, AC\( \bot \)DE (gt)
Vậy tứ giác ADCE là hình thoi.
c) Tam giác EAB nội tiếp đường tròn đường kính AB (gt)
Suy ra tam giác EAB vuông tại E hay EB\( \bot \)AE.
Ta có AE // CD (tứ giác ADCE là hình thoi) và EB\( \bot \)AE
Nên EB\( \bot \)CD.
Ta có EB\( \bot \)CD và FB\( \bot \)CD suy ra EB và FB trùng nhau.
Vậy ba điểm F, B, E thẳng hàng.
d) Tam giác FDE vuông tại F, FH là đường trung tuyến.
Suy ra FH = DH nên tam giác HFD cân tại H.
Do đó \(\widehat {HFD} = \widehat {HDC}\)
Mặt khác, O’F = O’C suy ra tam giác O’FC cân tại O’
Suy ra \(\widehat {O'FC} = \widehat {HCD}\)
Mà \(\widehat {HDC} = \widehat {HCD}\) và \(\widehat {HDC} + \widehat {HCD} = {90^o}\) (tam giác HCD vuông tại H)
Nên \(\widehat {HFD} + \widehat {O'FC} = {90^o}\)
Do đó \(\widehat {HFO'} = {180^o} - (\widehat {HFD} + \widehat {O'FC}) = {180^o} - {90^o} = {90^o}\)
Ta có HF\( \bot \)O’F, F thuộc đường tròn (O’).
Vậy HF là tiếp tuyến của đường tròn (O’).
Bài tập 14 trang 105 SGK Toán 9 tập 1 - Chân trời sáng tạo thuộc chương trình học về hàm số bậc nhất. Để giải bài tập này một cách hiệu quả, học sinh cần nắm vững các kiến thức cơ bản về hàm số, bao gồm định nghĩa, tính chất, cách xác định hàm số và ứng dụng của hàm số trong giải quyết các bài toán thực tế.
Bài tập 14 thường yêu cầu học sinh thực hiện các nhiệm vụ sau:
Để giải bài tập 14 trang 105 SGK Toán 9 tập 1 - Chân trời sáng tạo, bạn có thể thực hiện theo các bước sau:
Đề bài: Cho hàm số y = 2x + 3. Hãy xác định hệ số góc và tung độ gốc của hàm số.
Giải:
Hàm số y = 2x + 3 là hàm số bậc nhất có dạng y = ax + b, trong đó:
Ngoài bài tập 14, học sinh còn có thể gặp các dạng bài tập tương tự, như:
Để giải bài tập về hàm số bậc nhất một cách hiệu quả, bạn có thể áp dụng một số mẹo sau:
Hàm số bậc nhất là một trong những kiến thức cơ bản và quan trọng trong chương trình Toán 9. Việc học tốt hàm số bậc nhất sẽ giúp bạn:
Bài tập 14 trang 105 SGK Toán 9 tập 1 - Chân trời sáng tạo là một bài tập quan trọng giúp học sinh củng cố kiến thức về hàm số bậc nhất. Hy vọng với hướng dẫn chi tiết và các ví dụ minh họa trên đây, bạn sẽ tự tin giải bài tập này và đạt kết quả tốt trong môn Toán.