Giaitoan.edu.vn xin giới thiệu lời giải chi tiết bài tập 2 trang 87 SGK Toán 9 tập 2 - Chân trời sáng tạo. Bài viết này sẽ giúp học sinh nắm vững kiến thức, hiểu rõ phương pháp giải và tự tin làm bài tập.
Chúng tôi cung cấp đáp án chính xác, dễ hiểu cùng với các bước giải cụ thể, giúp bạn học Toán 9 một cách hiệu quả nhất.
Tìm chiều cao, bán kính đáy và diện tích xung quanh, thể tích của mỗi hình trụ sau:
Đề bài
Tìm chiều cao, bán kính đáy và diện tích xung quanh, thể tích của mỗi hình trụ sau:
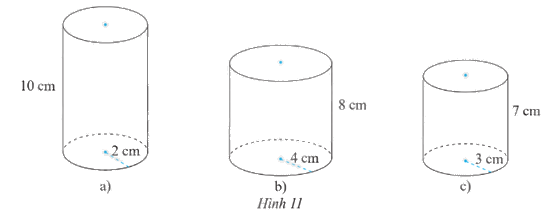
Video hướng dẫn giải
Phương pháp giải - Xem chi tiết
- Dựa vào: Khi quay hình chữ nhật AA’OO’ một vòng quanh cạnh OO’ cố định ta được một hình trụ.
+ Cạnh OA, O’A’ quét thành hai hình tròn có cùng bán kính gọi hai đáy của hình trụ; bán kính của đáy gọi là bán kính đáy của hình trụ.
+ Cạnh AA’ quét thành mặt xung quanh của hình trụ, mỗi vị trí của AA’ được coi là một đường sinh.
+ Độ dài OO’ gọi là chiều cao của hình cao. Các đường sinh có độ dài bằng nhau và bằng chiều cao hình trụ.
- Dựa vào Diện tích xung quanh của hình trụ là: \({S_{xq}} = 2\pi rh\)
- Dựa vào công thức thể tích của hình trụ: V = S.h = \(\pi \)r2h
Lời giải chi tiết
a) - Chiều cao: 10 cm.
- Bán kính đáy: 2 cm.
- Diện tích xung quanh là: \({S_{xq}} = 2\pi rh\) = 2\(\pi \).2.10 = 40\(\pi \) (cm2).
- Thể tích hình trụ là: V = S.h = \(\pi \)r2h =\(\pi \).22.10 = \(\pi \) (cm3).
b) - Chiều cao: 8 cm.
- Bán kính đáy: 4 cm.
- Diện tích xung quanh là: \({S_{xq}} = 2\pi rh\) = 2\(\pi \).4.8 = 64\(\pi \) (cm2).
- Thể tích hình trụ là: V = \(\pi \)r2h = \(\pi \).42.8 = 128\(\pi \) (cm3).
c) - Chiều cao: 7 cm.
- Bán kính đáy: 3 cm.
- Diện tích xung quanh là: \({S_{xq}} = 2\pi rh\) = 2\(\pi \).3.7 = 42\(\pi \) (cm2).
- Thể tích hình trụ là: V =\(\pi \)r2h =\(\pi \).32.7 = 63\(\pi \) (cm3).
Bài tập 2 trang 87 SGK Toán 9 tập 2 - Chân trời sáng tạo thuộc chương trình học Toán 9, tập trung vào việc vận dụng các kiến thức về hàm số bậc hai để giải quyết các bài toán thực tế. Để giải quyết bài tập này một cách hiệu quả, học sinh cần nắm vững các khái niệm cơ bản như:
Trước khi bắt tay vào giải bài tập, học sinh cần đọc kỹ đề bài, xác định rõ yêu cầu của bài toán và tìm ra hướng giải phù hợp. Trong bài tập 2 trang 87, yêu cầu thường là tìm các thông số của hàm số bậc hai dựa trên các điều kiện cho trước hoặc giải các phương trình, bất phương trình liên quan đến hàm số bậc hai.
Để giúp học sinh hiểu rõ hơn về cách giải bài tập này, chúng tôi sẽ trình bày lời giải chi tiết cho từng phần của bài tập. (Lưu ý: Nội dung lời giải chi tiết sẽ được trình bày cụ thể dựa trên nội dung bài tập 2 trang 87 SGK Toán 9 tập 2 - Chân trời sáng tạo. Do không có nội dung bài tập cụ thể, phần này sẽ được giữ chung chung.)
Giả sử đề bài cho hàm số y = 2x2 - 5x + 3. Khi đó:
Ngoài bài tập 2 trang 87, học sinh có thể gặp các dạng bài tập tương tự khác. Dưới đây là một số dạng bài tập thường gặp và phương pháp giải:
Để nắm vững kiến thức và kỹ năng giải bài tập về hàm số bậc hai, học sinh nên luyện tập thường xuyên với các bài tập khác nhau. Giaitoan.edu.vn cung cấp một kho bài tập phong phú, đa dạng với các mức độ khó khác nhau để bạn có thể luyện tập và củng cố kiến thức.
Bài tập 2 trang 87 SGK Toán 9 tập 2 - Chân trời sáng tạo là một bài tập quan trọng giúp học sinh hiểu rõ hơn về hàm số bậc hai và các ứng dụng của nó. Hy vọng với lời giải chi tiết và hướng dẫn cụ thể mà chúng tôi cung cấp, bạn sẽ tự tin hơn trong việc giải quyết các bài tập tương tự.
| Khái niệm | Giải thích |
|---|---|
| Hàm số bậc hai | Hàm số có dạng y = ax2 + bx + c, với a ≠ 0. |
| Đỉnh của parabol | Điểm thấp nhất (hoặc cao nhất) trên đồ thị hàm số bậc hai. |
| Trục đối xứng | Đường thẳng đi qua đỉnh của parabol và chia parabol thành hai phần đối xứng nhau. |