Bài tập 6 trang 97 SGK Toán 9 tập 1 thuộc chương Hàm số bậc nhất. Bài tập này yêu cầu học sinh vận dụng kiến thức về hàm số bậc nhất để giải quyết các bài toán thực tế. Giaitoan.edu.vn xin giới thiệu lời giải chi tiết, dễ hiểu, giúp các em học sinh nắm vững kiến thức và tự tin làm bài tập.
Chúng tôi luôn cập nhật nhanh chóng và chính xác các lời giải bài tập Toán 9 tập 1, tập 2, giúp các em học sinh có thêm tài liệu ôn tập và nâng cao kiến thức.
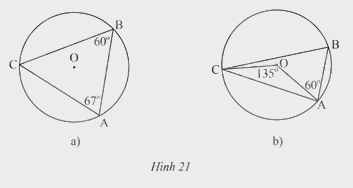
Xác định số đo các cung (oversetfrown{AB};oversetfrown{BC};oversetfrown{CA}) trong mỗi hình vẽ sau:
Đề bài
Xác định số đo các cung \(\overset\frown{AB};\overset\frown{BC};\overset\frown{CA}\) trong mỗi hình vẽ sau:
Video hướng dẫn giải
Phương pháp giải - Xem chi tiết
a) Dựa vào định lí: Trong một đường tròn, số đo của góc nội tiếp bằng nửa số đo cung bị chắn.
b) Số đo cung nhỏ bằng số đo của góc ở tâm chắn cung đó
Chứng minh tam giác OBA đều suy ra cung AB. Sau đó suy ra cung BC.
Lời giải chi tiết
a) Xét tam giác ABC, ta có: \(\widehat{ACB}={{180}^{o}}-\widehat{CBA}-\widehat{BAC}={{180}^{o}}-{{60}^{o}}-{{67}^{o}}={{53}^{o}}\)
Ta có sđ\(\overset\frown{AB}\) = 2.\(\widehat{ACB}\) = 2. 53o = 106o (Vì \(\widehat{ACB}\) là góc nội tiếp chắn cung AB)
Ta có sđ\(\overset\frown{BC}\) = 2.\(\widehat{BAC}\) = 2. 67o = 134o (Vì \(\widehat{BAC}\) là góc nội tiếp chắn cung BC)
Ta có sđ\(\overset\frown{AC}\) = 2.\(\widehat{ABC}\) = 2. 60o = 120o (Vì \(\widehat{ABC}\) là góc nội tiếp chắn cung AC).
b) Ta có sđ\(\overset\frown{AC}\) và góc ở tâm \(\widehat{COA}\) cùng chắn cung AC
suy ra sđ\(\overset\frown{AC}\) = \(\widehat{COA}\) = 135o.
Nối O với B.
Xét tam giác OAB có AO = OB (= R) suy ra tam giác OAB cân tại A.
Mặt khác, \(\widehat {OAB} = {60^o}\) nên tam giác OAB là tam giác đều.
Ta có sđ\(\overset\frown{AB}\) = \(\widehat{AOB}\) = \({{60}^{o}}\) (Vì \(\widehat{AOB}\) là góc nội tiếp chắn cung AB)
Suy ra sđ\(\overset\frown{BC}\) = 360o - sđ\(\overset\frown{AB}\) - sđ\(\overset\frown{AC}\) = 360o - \({60^o}\) - 135o = 165o.
Bài tập 6 trang 97 SGK Toán 9 tập 1 - Chân trời sáng tạo là một bài toán ứng dụng thực tế về hàm số bậc nhất. Để giải bài tập này, học sinh cần nắm vững các khái niệm về hàm số bậc nhất, cách xác định hệ số góc và tung độ gốc, cũng như cách vẽ đồ thị hàm số.
Một người đi xe đạp với vận tốc không đổi là 15 km/h. Quãng đường đi được của người đó theo thời gian được biểu diễn bằng hàm số nào?
Bài toán yêu cầu chúng ta xác định hàm số biểu diễn mối quan hệ giữa quãng đường đi được và thời gian. Chúng ta biết rằng quãng đường đi được bằng vận tốc nhân với thời gian. Trong trường hợp này, vận tốc là hằng số (15 km/h).
Gọi s là quãng đường đi được (km) và t là thời gian (giờ). Ta có hàm số biểu diễn quãng đường đi được của người đó theo thời gian là:
s = 15t
Hàm số này là một hàm số bậc nhất với hệ số góc là 15 và tung độ gốc là 0.
Hệ số góc 15 cho biết vận tốc của người đi xe đạp (15 km/h). Tung độ gốc 0 cho biết khi thời gian bằng 0, quãng đường đi được cũng bằng 0 (điều này hợp lý).
Nếu người đó đi xe đạp trong 2 giờ, quãng đường đi được là:
s = 15 * 2 = 30 km
Ngoài bài tập 6 trang 97, SGK Toán 9 tập 1 - Chân trời sáng tạo còn có nhiều bài tập khác liên quan đến hàm số bậc nhất. Một số dạng bài tập tương tự bao gồm:
Để giải tốt các bài tập về hàm số bậc nhất, bạn nên:
Bài tập 6 trang 97 SGK Toán 9 tập 1 - Chân trời sáng tạo là một bài toán ứng dụng thực tế về hàm số bậc nhất. Việc hiểu rõ các khái niệm và phương pháp giải bài tập này sẽ giúp bạn học tốt môn Toán 9 và áp dụng kiến thức vào thực tế.
| Khái niệm | Mô tả |
|---|---|
| Hàm số bậc nhất | Hàm số có dạng y = ax + b, trong đó a và b là các số thực, a ≠ 0. |
| Hệ số góc | Số a trong hàm số y = ax + b. |
| Tung độ gốc | Số b trong hàm số y = ax + b. |
| Đồ thị hàm số bậc nhất | Đường thẳng đi qua hai điểm (0, b) và (-b/a, 0). |
Hy vọng với lời giải chi tiết và những kiến thức bổ ích trên, các em học sinh sẽ tự tin hơn khi giải bài tập 6 trang 97 SGK Toán 9 tập 1 - Chân trời sáng tạo và các bài tập tương tự khác.