Chào mừng bạn đến với bài học về Lý thuyết Bất đẳng thức Toán 9 Chân trời sáng tạo trên giaitoan.edu.vn. Bài học này sẽ cung cấp cho bạn những kiến thức nền tảng và các quy tắc quan trọng về bất đẳng thức, giúp bạn giải quyết các bài toán một cách hiệu quả.
Chúng tôi sẽ trình bày lý thuyết một cách rõ ràng, dễ hiểu, kèm theo các ví dụ minh họa cụ thể. Đồng thời, bạn sẽ được làm quen với các dạng bài tập thường gặp và phương pháp giải quyết chúng.
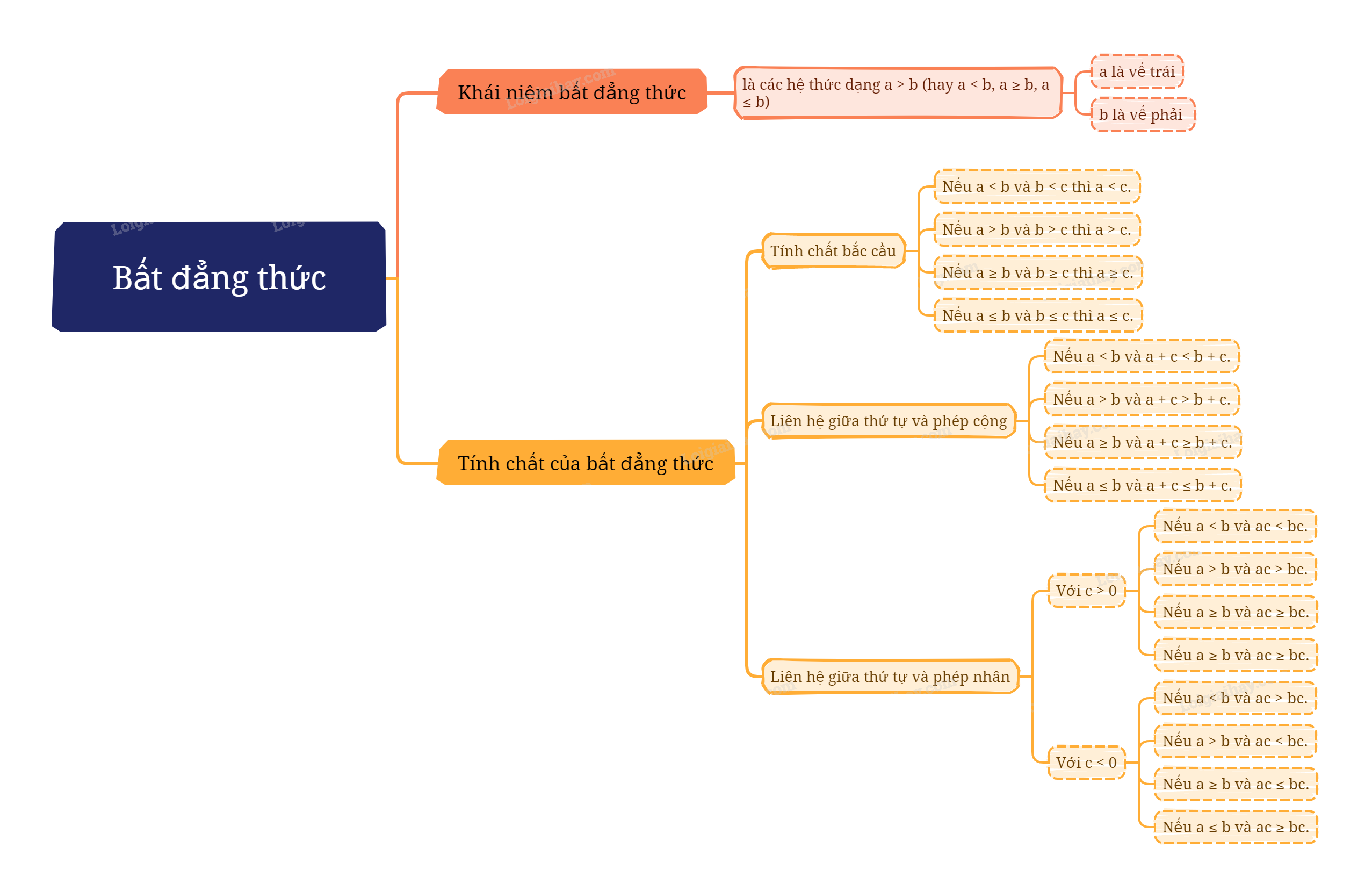
1. Bất đẳng thức Nhắc lại thứ tự trên tập số thực
1. Bất đẳng thức
Nhắc lại thứ tự trên tập số thực
Trên tập số thực, khi so sánh hai số a và b, xảy ra một trong ba trường hợp sau:
- Số a lớn hơn số b, kí hiệu \(a > b\).
- Số a nhỏ hơn số b, kí hiệu \(a < b\).
- Số a bằng số b, kí hiệu \(a = b\).
Khi biểu diễn số thực trên trục số, điểm biểu diễn số bé hơn nằm trước điểm biểu diễn số lớn hơn.
Nếu \(a > b\) hoặc \(a = b\), ta viết \(a \ge b\) (ta nói a lớn hơn hoặc bằng b hay a không nhỏ hơn b).
Nếu \(a < b\) hoặc \(a = b\), ta viết \(a \le b\) (ta nói a nhỏ hơn hoặc bằng b hay a không lớn hơn b).
Khái niệm bất đẳng thức
Hệ thức dạng \(a > b\) (hay \(a < b\), \(a \ge b\), \(a \le b\)) là bất đẳng thức và a được gọi là vế trái, b được gọi là vế phải của bất đẳng thức. |
2. Tính chất của bất đẳng thức
Tính chất bắc cầu
Cho ba số a, b, c. Nếu \(a < b\) và \(b < c\) thì \(a < c\). Nếu \(a > b\) và \(b > c\) thì \(a > c\). Nếu \(a \le b\) và \(b \le c\) thì \(a \le c\). Nếu \(a \ge b\) và \(b \ge c\) thì \(a \ge c\). |
Ví dụ: Vì \(\frac{{2024}}{{2023}} = 1 + \frac{1}{{2023}} > 1\) và \(\frac{{2021}}{{2022}} = 1 - \frac{1}{{2022}} < 1\) nên \(\frac{{2024}}{{2023}} > \frac{{2021}}{{2022}}\).
Tính chất liên hệ giữa thứ tự và phép cộng
Khi cộng cùng một số vào hai vế của một bất đẳng thức ta được bất đẳng thức mới cùng chiều với bất đẳng thức đã cho.
Cho ba số a, b, c. Nếu \(a < b\) thì \(a + c < b + c\). Nếu \(a > b\) thì \(a + c > b + c\). Nếu \(a \le b\) thì \(a + c \le b + c\). Nếu \(a \ge b\) thì \(a + c \ge b + c\). |
Ví dụ:Vì \(2023 < 2024\) nên \(2023 + \left( { - 19} \right) < 2024 + \left( { - 19} \right)\)
Tính chất liên hệ giữa thứ tự và phép nhân
- Khi nhân cả hai vế của một bất đẳng thức với cùng một số dương ta được bất đẳng thức mới cùng chiều với bất đẳng thức đã cho.
Với ba số a, b, c và c > 0, ta có: Nếu \(a < b\) thì \(ac < bc\). Nếu \(a > b\) thì \(ac > bc\). Nếu \(a \le b\) thì \(ac \le bc\). Nếu \(a \ge b\) thì \(ac \ge bc\). |
- Khi nhân cả hai vế của một bất đẳng thức với cùng một số âm ta được bất đẳng thức mới ngược chiều với bất đẳng thức đã cho.
Với ba số a, b, c và c < 0, ta có: Nếu \(a < b\) thì \(ac > bc\). Nếu \(a > b\) thì \(ac < bc\). Nếu \(a \le b\) thì \(ac \ge bc\). Nếu \(a \ge b\) thì \(ac \le bc\). |
Ví dụ:
Vì \( - 7 < - 5\) và \(3 > 0\) nên \(3.\left( { - 7} \right) < 3.\left( { - 5} \right)\).
Vì \( - 7 < - 5\) và \( - 3 < 0\) nên \(\left( { - 3} \right).\left( { - 7} \right) > \left( { - 3} \right).\left( { - 5} \right)\).
Bất đẳng thức là một khái niệm quan trọng trong toán học, đặc biệt là ở chương trình Toán 9. Hiểu rõ lý thuyết và các quy tắc liên quan đến bất đẳng thức là nền tảng để giải quyết các bài toán phức tạp hơn trong tương lai.
Bất đẳng thức là một biểu thức toán học so sánh hai giá trị, sử dụng các ký hiệu: >, <, ≥, ≤, ≠. Ví dụ: a > b (a lớn hơn b), x < 5 (x nhỏ hơn 5).
Có một số tính chất quan trọng của bất đẳng thức mà bạn cần nắm vững:
Trong chương trình Toán 9, bạn sẽ gặp một số loại bất đẳng thức thường gặp:
Để giải bất đẳng thức, bạn cần thực hiện các bước sau:
Ví dụ 1: Giải bất đẳng thức 2x + 3 > 7
Giải:
2x + 3 > 7
2x > 4
x > 2
Vậy nghiệm của bất đẳng thức là x > 2.
Ví dụ 2: Giải bất đẳng thức (x - 1)(x + 2) < 0
Giải:
(x - 1)(x + 2) < 0
Bất đẳng thức này có nghiệm khi (x - 1) và (x + 2) trái dấu.
Trường hợp 1: x - 1 > 0 và x + 2 < 0
=> x > 1 và x < -2 (vô lý)
Trường hợp 2: x - 1 < 0 và x + 2 > 0
=> x < 1 và x > -2
-2 < x < 1
Vậy nghiệm của bất đẳng thức là -2 < x < 1.
Để nắm vững kiến thức về bất đẳng thức, bạn nên luyện tập thường xuyên với các bài tập khác nhau. Hãy tìm các bài tập trong sách giáo khoa, sách bài tập hoặc trên các trang web học toán online như giaitoan.edu.vn.
Lý thuyết Bất đẳng thức Toán 9 Chân trời sáng tạo là một phần quan trọng của chương trình học. Việc hiểu rõ các khái niệm, tính chất và phương pháp giải bất đẳng thức sẽ giúp bạn tự tin hơn khi giải các bài toán và đạt kết quả tốt trong các kỳ thi.