Phương trình bậc hai một ẩn là một trong những kiến thức trọng tâm của chương trình Toán 9, đặc biệt trong sách Chân Trời Sáng Tạo. Việc nắm vững lý thuyết và phương pháp giải phương trình bậc hai là nền tảng quan trọng cho các bài toán nâng cao và các chương trình học tiếp theo.
Tại giaitoan.edu.vn, chúng tôi cung cấp bài học lý thuyết chi tiết, dễ hiểu, kèm theo các ví dụ minh họa và bài tập thực hành đa dạng, giúp học sinh hiểu sâu sắc và vận dụng thành thạo kiến thức về phương trình bậc hai.
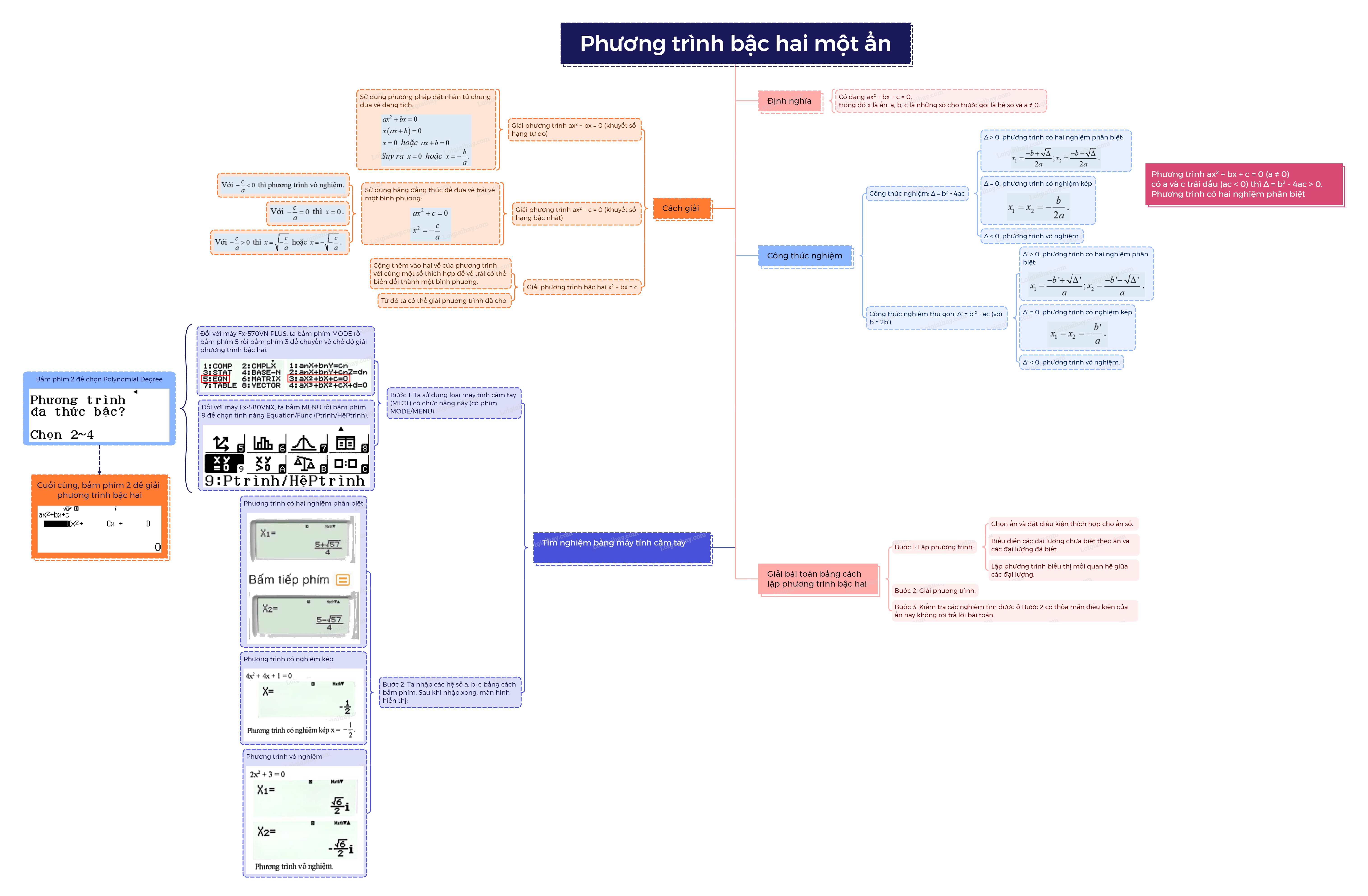
1. Định nghĩa phương trình bậc hai một ẩn Phương trình bậc hai một ẩn (còn gọi là phương trình bậc hai) là phương trình có dạng \(a{x^2} + bx + c = 0\), trong đó x là ẩn; a, b, c là những số cho trước gọi là các hệ số và \(a \ne 0\).
1. Định nghĩa phương trình bậc hai một ẩn
Phương trình bậc hai một ẩn (còn gọi là phương trình bậc hai) là phương trình có dạng \(a{x^2} + bx + c = 0\), trong đó x là ẩn; a, b, c là những số cho trước gọi là các hệ số và \(a \ne 0\). |
Ví dụ: Phương trình \(2{x^2} - 3x + 1 = 0\) là phương trình bậc hai với \(a = 2;b = - 3;c = 1\).
Phương trình \({x^2} - 3 = 0\) là phương trình bậc hai với \(a = 1,b = 0,c = - 3\).
Phương trình \(0{x^2} - 2x - 3 = 0\) không là phương trình bậc hai vì \(a = 0\).
2. Giải một số phương trình bậc hai dạng đặc biệt
Giải phương trình bậc hai khuyết số hạng tự do (dạng \(a{x^2} + bx = 0\)\(\left( {a \ne 0,c = 0} \right)\))
Để giải phương trình bậc hai dạng \(a{x^2} + bx = 0\), ta sử dụng phương pháp đặt nhân tử chung đưa về dạng tích. \(\begin{array}{l}a{x^2} + bx = 0\\x\left( {ax + b} \right) = 0\end{array}\) \(x = 0\) hoặc \(ax + b = 0\) Suy ra \(x = 0\) hoặc \(x = - \frac{b}{a}\). |
Ví dụ: Giải phương trình \(2{x^2} - 4x = 0\)
Ta có:
\(\begin{array}{l}2{x^2} - 4x = 0\\2x\left( {x - 2} \right) = 0\end{array}\)
\(x = 0\) hoặc \(x - 2 = 0\)
\(x = 0\) hoặc \(x = 2\).
Vậy phương trình có hai nghiệm \({x_1} = 0,{x_2} = 2\).
Giải phương trình bậc hai khuyết số hạng bậc nhất (dạng \(a{x^2} + c = 0\)\(\left( {a \ne 0,b = 0} \right)\))
Để giải phương trình bậc hai dạng \(a{x^2} + c = 0\), ta sử dụng hằng đẳng thức để dưa vế trái về một bình phương: \(\begin{array}{l}a{x^2} + c = 0\\{x^2} = - \frac{c}{a}\end{array}\) +) Với \( - \frac{c}{a} < 0\) thì phương trình vô nghiệm. +) Với \( - \frac{c}{a} = 0\) thì \(x = 0\). +) Với \( - \frac{c}{a} > 0\) thì \(x = \sqrt { - \frac{c}{a}} \) hoặc \(x = - \sqrt { - \frac{c}{a}} \). |
Ví dụ: 1. Giải phương trình \({x^2} - 9 = 0\)
Ta có:
\(\begin{array}{l}{x^2} - 9 = 0\\{x^2} = 9\end{array}\)
\(x = 3\) hoặc \(x = - 3\)
Vậy phương trình có hai nghiệm \({x_1} = 3,{x_2} = - 3\).
2. Giải phương trình \({\left( {x + 1} \right)^2} = 3\)
Ta có: \({\left( {x + 1} \right)^2} = 3\)
\(x + 1 = \sqrt 3 \) hoặc \(x + 1 = - \sqrt 3 \)
\(x = - 1 + \sqrt 3 \) hoặc \(x = - 1 - \sqrt 3 \)
Vậy phương trình có hai nghiệm \({x_1} = - 1 + \sqrt 3 ,{x_2} = - 1 - \sqrt 3 \).
Giải phương trình bậc hai dạng \({x^2} + bx = c\)
Để giải phương trình bậc hai dạng \({x^2} + bx = c\), ta có thể cộng thêm vào hai vế của phương trình với cùng một số thích hợp để vế trái có thể biến đổi thành một bình phương. Từ đó ta có thể giải phương trình đã cho. |
Ví dụ: Giải phương trình \({x^2} - 4x = 1\)
Ta có:
\(\begin{array}{l}{x^2} - 4x = 5\\{x^2} - 4x + 4 = 5 + 4\\{\left( {x - 2} \right)^2} = 9\end{array}\)
\(x - 2 = 3\) hoặc \(x - 2 = - 3\)
suy ra \(x = 5\) hoặc \(x = - 1\).
Vậy phương trình có hai nghiệm \({x_1} = 5,{x_2} = - 1\).
3. Công thức nghiệm của phương trình bậc hai
Công thức nghiệm của phương trình bậc hai:
Cho phương trình \(a{x^2} + bx + c = 0\left( {a \ne 0} \right)\) và biệt thức \(\Delta = {b^2} - 4ac\). - Nếu \(\Delta > 0\) thì phương trình có hai nghiệm phân biệt: \({x_1} = \frac{{ - b + \sqrt \Delta }}{{2a}};{x_2} = \frac{{ - b - \sqrt \Delta }}{{2a}}\). - Nếu \(\Delta = 0\) thì phương trình có nghiệm kép \({x_1} = {x_2} = - \frac{b}{{2a}}\). - Nếu \(\Delta < 0\) thì phương trình vô nghiệm. |
Ví dụ: Giải phương trình \({x^2} - 7x - 8 = 0\).
Ta có: \(a = 1,b = - 7,c = - 8\).
\(\Delta = {b^2} - 4ac = {\left( { - 7} \right)^2} - 4.1.\left( { - 8} \right) = 81 > 0\).
Vậy phương trình có hai nghiệm phân biệt là
\({x_1} = \frac{{ - \left( { - 7} \right) + \sqrt {81} }}{{2.1}} = 8;{x_2} = \frac{{ - \left( { - 7} \right) - \sqrt {81} }}{{2.1}} = - 1\).
Chú ý: Nếu phương trình \(a{x^2} + bx + c = 0\left( {a \ne 0} \right)\) có a và c trái dấu, tức là \(ac < 0\), thì \(\Delta = {b^2} - 4ac > 0\). Khi đó, phương trình có hai nghiệm phân biệt.
Ví dụ: Phương trình \({x^2} + 3572x - 3573 = 0\) có \(a = 1 > 0,c = - 3573 < 0\), suy ra a và c trái dấu.
Do đó phương trình có hai nghiệm phân biệt.
Công thức nghiệm thu gọn của phương trình bậc hai:
Xét phương trình bậc hai một ẩn \(a{x^2} + bx + c = 0\left( {a \ne 0} \right)\), với \(b = 2b'\) và \(\Delta ' = b{'^2} - ac\). - Nếu \(\Delta ' > 0\) thì phương trình có hai nghiệm phân biệt: \({x_1} = \frac{{ - b' + \sqrt {\Delta '} }}{a};{x_2} = \frac{{ - b' - \sqrt {\Delta '} }}{a}\). - Nếu \(\Delta ' = 0\) thì phương trình có nghiệm kép \({x_1} = {x_2} = - \frac{{b'}}{a}\). - Nếu \(\Delta ' < 0\) thì phương trình vô nghiệm. |
Ví dụ: Giải phương trình \(7{x^2} - 12x + 5 = 0\).
Ta có: \(a = 7,b' = - 6,c = 5\).
\(\Delta ' = b{'^2} - ac = {\left( { - 6} \right)^2} - 7.5 = 1 > 0\).
Vậy phương trình có hai nghiệm phân biệt là
\({x_1} = \frac{{ - \left( { - 6} \right) + 1}}{7} = 1;{x_2} = \frac{{ - \left( { - 6} \right) - 1}}{7} = \frac{5}{7}\).
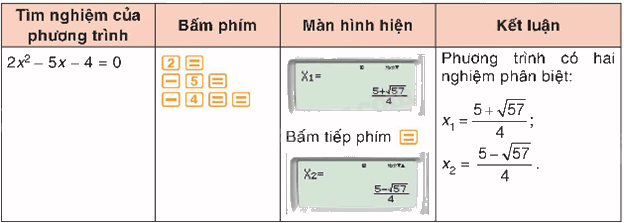
3. Tìm nghiệm của phương trình bậc hai bằng máy tính cầm tay
Sử dụng máy tính cầm tay, ta có thể dễ dạng tìm nghiệm của các phương trình bậc hai.
Bước 1. Ta sử dụng loại máy tính cầm tay (MTCT) có chức năng này (có phím MODE/MENU).
- Đối với máy Fx-570VN PLUS, ta bấm phím MODE rồi bấm phím 5 rồi bấm phím 3 để chuyển về chế độ giải phương trình bậc hai.

- Đối với máy Fx-580VNX, ta bấm MENU rồi bấm phím 9 để chọn tính năng Equation/Func (Ptrình/HệPtrình).
Bấm phím 2 để chọn Polynomial Degree
Cuối cùng, bấm phím 2 để giải phương trình bậc hai
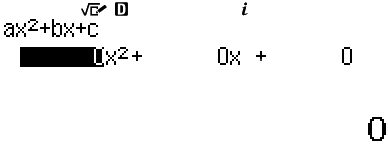
Bước 2. Ta nhập các hệ số \(a,b,c\) bằng cách bấm
Đối với phương trình bậc hai có nghiệm kép, ta nhận được kết quả hiển thị trên màn hình như sau:

Đối với phương trình bậc hai vô nghiệm, ta nhận được kết quả hiển thị trên màn hình như sau:

5. Giải bài toán bằng cách lập phương trình bậc hai
Bước 1: Lập phương trình: - Chọn ẩn và đặt điều kiện thích hợp cho ẩn số. - Biểu diễn các đại lượng chưa biết theo ẩn và các đại lượng đã biết. - Lập phương trình biểu thị mối quan hệ giữa các đại lượng. Bước 2. Giải phương trình. Bước 3. Kiểm tra các nghiệm tìm được ở Bước 2 có thỏa mãn điều kiện của ẩn hay không rồi trả lời bài toán. |
Ví dụ: Một ca nô xuất phát từ một bến và có chuyển động thẳng theo hướng Đông. Cùng lúc đó, một tàu thủy rời bến và chuyển động thẳng theo hướng Nam với tốc độ lớn hơn tốc độ của ca nô 8km/h. Tính tốc độ của ca nô, biết sau một giờ kể từ lúc xuất phát, khoảng cách giữa ca nô với tàu thủy là 40km.
Lời giải:
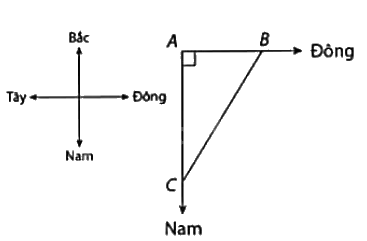
Gọi tốc độ của ca nô là \(x\left( {km/h} \right)\left( {x > 0} \right)\).
Tốc độ của tàu thủy là \(x + 8\left( {km/h} \right)\).
Gọi A là vị trí của bến, gọi B, C lần lượt là vị trí của ca nô và tàu thủy sau khi rời bến 1 giờ (như hình vẽ).
Quãng đường ca nô đi được sau 1 giờ là:
\(AB = x.1 = x\left( {km} \right)\)
Quãng đường tàu thủy đi được sau 1 giờ là:
\(AC = \left( {x + 8} \right).1 = x + 8\left( {km} \right)\)
Ca nô và tày thủy chuyển động theo hai hướng vuông góc với nhau nên tam giác ABC vuông tại A.
Ta có: \(A{B^2} + A{C^2} = B{C^2}\) (định lí Pythagore).
\(\begin{array}{l}{x^2} + {\left( {x + 8} \right)^2} - {40^2}\\{x^2} + {x^2} + 16x + 64 = 1600\\2{x^2} + 16x - 1536 = 0\\{x^2} + 8x - 768 = 0\end{array}\)
Ta có: \(\Delta ' = {4^2} + 768 = 784,\sqrt {\Delta '} = 28\).
Suy ra phương trình có hai nghiệm phân biệt:
\({x_1} = \frac{{ - 4 - 28}}{1} = - 32\) (loại); \({x_2} = \frac{{ - 4 + 28}}{1} = 24\) (thỏa mãn điều kiện).
Vậy tốc độ của ca nô là \(24km/h\).
Phương trình bậc hai một ẩn là phương trình có dạng tổng quát: ax² + bx + c = 0, trong đó a, b, c là các số thực và a ≠ 0. Đây là một trong những chủ đề quan trọng trong chương trình Toán 9, đặc biệt là sách giáo khoa Chân Trời Sáng Tạo. Việc hiểu rõ lý thuyết và các phương pháp giải phương trình bậc hai là nền tảng vững chắc cho việc giải quyết các bài toán phức tạp hơn trong tương lai.
Để hiểu rõ về phương trình bậc hai, chúng ta cần nắm vững các thành phần cấu tạo của nó:
Ví dụ: Trong phương trình 2x² - 5x + 3 = 0, ta có a = 2, b = -5, và c = 3.
Có một số dạng phương trình bậc hai đặc biệt cần được chú ý:
Để giải phương trình bậc hai, chúng ta sử dụng công thức nghiệm tổng quát:
x = (-b ± √(b² - 4ac)) / 2a
Trong đó:
Biệt thức Δ đóng vai trò quan trọng trong việc xác định số nghiệm của phương trình bậc hai:
Ngoài công thức nghiệm tổng quát, còn có một số phương pháp giải phương trình bậc hai khác:
Phương trình bậc hai có rất nhiều ứng dụng trong thực tế, ví dụ như:
Để củng cố kiến thức, hãy giải các bài tập sau:
Lý thuyết phương trình bậc hai một ẩn là một phần quan trọng của chương trình Toán 9 Chân Trời Sáng Tạo. Việc nắm vững lý thuyết, công thức và các phương pháp giải phương trình bậc hai sẽ giúp học sinh tự tin giải quyết các bài toán và ứng dụng kiến thức vào thực tế. Hãy luyện tập thường xuyên để đạt kết quả tốt nhất!