Chào mừng bạn đến với giaitoan.edu.vn, nơi cung cấp lời giải chi tiết và dễ hiểu cho các bài tập Toán 9. Bài viết này sẽ hướng dẫn bạn giải quyết hoàn toàn mục 1 trang 75 SGK Toán 9 tập 1 - Chân trời sáng tạo, giúp bạn nắm vững kiến thức và tự tin hơn trong quá trình học tập.
Chúng tôi luôn cố gắng cung cấp nội dung chính xác, đầy đủ và cập nhật nhất để hỗ trợ bạn học Toán 9 một cách hiệu quả.
Mở 1 chiếc compa sao cho hai đầu compa cách nhau một khoảng R cho trước. Tì đầu nhọn của compa lên một điểm cố định trên tờ giấy, xoay compa để đầu bút M của compa vạch trên giấy một đường cong. Nêu nhận xét về các khoảng cách từ một điểm M tuỳ ý trên đường cong vừa vẽ đến điểm O.
Đề bài
Trả lời câu hỏi Hoạt động 1 trang 75SGK Toán 9 Chân trời sáng tạo
Mở 1 chiếc compa sao cho hai đầu compa cách nhau một khoảng R cho trước. Tì đầu nhọn của compa lên một điểm cố định trên tờ giấy, xoay compa để đầu bút M của compa vạch trên giấy một đường cong. Nêu nhận xét về các khoảng cách từ một điểm M tuỳ ý trên đường cong vừa vẽ đến điểm O.
Video hướng dẫn giải
Phương pháp giải - Xem chi tiết
Đọc kĩ dữ liệu đề bài để vẽ hình, sau đó nhận xét.
Lời giải chi tiết
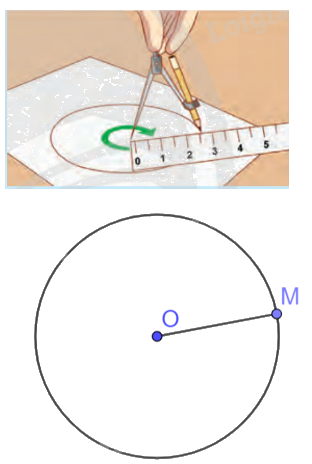
Nhận xét: Khoảng cách từ một điểm M tuỳ ý trên đường cong vừa vẽ đến điểm O không thay đổi.
Mục 1 trang 75 SGK Toán 9 tập 1 - Chân trời sáng tạo thường xoay quanh các bài tập về hàm số bậc nhất, bao gồm việc xác định hệ số góc, phương trình đường thẳng, và ứng dụng của hàm số trong việc giải quyết các bài toán thực tế. Việc nắm vững kiến thức về hàm số bậc nhất là nền tảng quan trọng cho các chương trình học Toán ở các lớp trên.
Để giải quyết mục 1 trang 75 SGK Toán 9 tập 1 - Chân trời sáng tạo một cách hiệu quả, chúng ta cần nắm vững các kiến thức sau:
Dưới đây là hướng dẫn giải chi tiết từng bài tập trong mục 1 trang 75 SGK Toán 9 tập 1 - Chân trời sáng tạo:
Để xác định hệ số góc của đường thẳng, bạn cần đưa phương trình đường thẳng về dạng y = ax + b. Sau đó, hệ số a chính là hệ số góc của đường thẳng.
Ví dụ: Cho đường thẳng có phương trình 2x + 3y - 1 = 0. Để tìm hệ số góc, ta biến đổi phương trình về dạng y = ax + b:
3y = -2x + 1
y = (-2/3)x + 1/3
Vậy hệ số góc của đường thẳng là -2/3.
Để viết phương trình đường thẳng đi qua hai điểm A(x1, y1) và B(x2, y2), ta thực hiện các bước sau:
Ví dụ: Viết phương trình đường thẳng đi qua hai điểm A(1, 2) và B(3, 4).
Hệ số góc m = (4 - 2) / (3 - 1) = 1.
Phương trình đường thẳng là: y - 2 = 1(x - 1) hay y = x + 1.
Để tìm giao điểm của hai đường thẳng, ta giải hệ phương trình gồm phương trình của hai đường thẳng đó. Nghiệm của hệ phương trình chính là tọa độ giao điểm của hai đường thẳng.
Ví dụ: Tìm giao điểm của hai đường thẳng y = x + 1 và y = -x + 3.
Giải hệ phương trình:
{ y = x + 1y = -x + 3 }
Thay y = x + 1 vào phương trình y = -x + 3, ta được:
x + 1 = -x + 3
2x = 2
x = 1
Thay x = 1 vào phương trình y = x + 1, ta được y = 2.
Vậy giao điểm của hai đường thẳng là (1, 2).
Hy vọng với hướng dẫn chi tiết này, bạn đã có thể tự tin giải quyết mục 1 trang 75 SGK Toán 9 tập 1 - Chân trời sáng tạo. Chúc bạn học tập tốt!